Students can Download 1st PUC Basic Maths Previous Year Question Paper March 2016 (South), Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.
Karnataka 1st PUC Basic Maths Previous Year Question Paper March 2016 (South)
Time: 3.15 Hours
Max. Marks: 100
Instructions:
- The questions paper consists of five parts A, B, C, D, and E.
- Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
- Write the question numbers properly as indicated in the questions paper
PART-A
I. Answer any TEN questions. (10 × 1 = 10)
Question 1.
Give the canonical representation of 385.
Answer:
385 = 5′ × 71 × 111
Question 2.
If R = {(1, 2), (2, 3), (3, 3} a relation defined on the set A = {1, 2, 3} find R-1.
Answer:
R-1 = {(2, 1), (3,2), (3, 3)}
Question 3.
If A = (3, 5, 7}, B = {7, 9, 11} find B-A.
Answer:
B – A = {9, 11}
Question 4.
Simplify \(\sqrt[4]{x^{-4 / 3}}\)
Answer:
(x-4/3)1/4 = x-1/3 = x1/1/3 = \(\frac{1}{\sqrt[3]{x}}\)
Question 5.
Find the value of x if log\(\sqrt{2}\) x = 4
Answer:
(\(\sqrt{2}\))4 = x ⇒ x = 22 ⇒ x = 4
![]()
Question 6.
Find the 8th term of the sequence 1, \(\frac{1}{2}\), \(\frac{1}{3}\)
Answer:
T8 = \(\frac{1}{8}\)
Question 7.
Form a quadratic equation with roots ‘O’ and ‘-1′
Answer:
(x – 0)(x + 1) = 0 ⇒ x2 + x= 0
Question 8.
What is the simple interest on Rs. 1000 for half a year at 10% p.a.?
Answer:
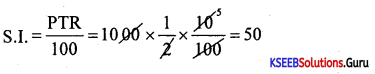
Question 9.
The sum of the ages of 10 girls in a class is 120 years. If one more girl of age 1 year is added to the group, find the average of 11 girls.
Answer:
X̄11 = \(\frac{120+1}{11}=\frac{121}{11}\) = 11yrs
Question 10.
Convert 15% to the ratio form.
Answer:
3:20
Question 11.
Write the value of cosec2 10° – cot210°.
Answer:
cosec210 – cot210 = 1
Question 12.
Find the distance from the origin to the line 3x – 4y + 5 = 0.
Answer:
\(\frac{5}{\sqrt{3^{2}+4^{2}}}=\frac{5}{\sqrt{25}}=\frac{5}{5}\) = 1
PART-B
II. Answer any TEN questions: (10 × 2 = 20)
Question 13.
Find the total number of positive divisors of 180.
Answer:
180 = 22 × 32 × 5
T(180) = (2 + 1) (2 + 1) (1 + 1) = 3 × 3 × 2 = 18
Question 14.
If f(x) = x2, g(x) = x – 1, find go f(x) and gof(a).
Answer:
gof (x) = gf(x) = g(x2) = x2 – 1
gof(a) = a2 – 1
![]()
Question 15.
Simplify: \(\frac{2^{7 a-2 b} \cdot 8^{2 a-b}}{16^{a+b}}\)
Answer:
\(\frac{2^{7 a-2 b} \cdot\left(2^{3}\right)^{2 a-b}}{\left(2^{4}\right)^{a+b}}=\frac{2^{7 a-2 b} \cdot 2^{6 a-3 b}}{2^{4 a+4 b}}\) = 27a-2b+a-3b-4a-4b = 29a-9b
Question 16.
Prove that log \(\sqrt{a / b}\) + log \(\sqrt{b / c}+\) + log \(\sqrt{c / a}+\) = 0
Answer:
LHS = \(\frac{1}{2}\)log\(\frac{a}{b}\) + \(\frac{1}{2}\)log\(\frac{b}{c}\) + \(\frac{1}{2}\)log\(\frac{c}{a}\)
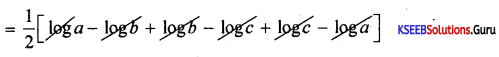
= \(\frac{1}{2}\) × 0 = 0 = R.H.S
Question 17.
Find the sum to infinity of GP. 3, -1, \(\frac{1}{3}\), –\(\frac{1}{9}\) ………. if it exists.
Answer:
S∞ = \(\frac{a}{1-r}\) Given a = 3, r = –\(\frac{1}{3}\)
S∞ = \(\frac{3}{1+\frac{1}{3}}=\frac{9}{4}\)
Question 18.
Find two numbers whose sum is 64 and the difference is 16.
Answer:
Let 2 numbers be x and y
∴ Given x + y = 64 & x – y = 16
Solving the above equations we get
x = 40 & y = 24
∴ The two numbers are 24 and 40
Question 19.
Solve the unequalities 5x – 3 > 3x + 1, x∈R and represent on the number line.
Answer:
5x – 3 > 3x + 1 & x ∈ R

5x – 3x > 1 + 3
2x > 4 ⇒ x > 2
Question 20.
A certain sum of money amounts to Rs.24,200 in 2 years
Answer:
Given F = 24,200, n = 2yrs r = 10%, P = ?
F = P(i + r)n
P = \(\frac{\mathrm{F}}{(1+r)^{n}}=\frac{24,200}{(1+0.1)^{2}}=\frac{24,200}{(1.1)^{2}}\) = ₹20,000
∴ The Sum = ₹20,000
Question 21.
Ram and Shyam went up a hill at a speed of 20kmph. Both of them came tumbling down the same distance at a speed of 30 km ph. Find the average speed for the round trip.
Answer:
Average speed = \(\frac{2 d}{\frac{d}{20}+\frac{d}{30}}=\frac{2 d}{\frac{5 d}{60}}=\frac{120}{5}\) = 24 kmph
Question 22.
While taking measurement a tailor writes 34 instead of 24. What is the percentage error?
Answer:
For 24 → 10 Errors
∴ 100 → ?
\(\frac{10 \times 100}{24}\) = 41.66
Hence percentage error = 41.66
Question 23.
If tan A = 5/12 acute find the value of \(\frac{\sin A+\cos A}{\sin A-\cos A}\)
Answer:
Given tan A = \(\frac{5}{12}=\frac{\mathrm{opp}}{\mathrm{adj}}\)
∴ HYP = \(\sqrt{12^{2}+5^{2}}=\sqrt{169}\) = 13
∴ sinA = \(\frac{5}{13}\), & cos A = \(\frac{12}{13}\)
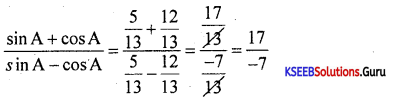
Question 24.
Show that the points A(4, -2), B(2, -4), and C(7, 1) are collinear using the slope method.
Answer:
A(4, -2) B(2, -4) C(7, 1)
Slope AB = \(\frac{y_{2}-y_{1}}{y_{2}-x_{1}}=\frac{-4-(-2)}{2-4}=\frac{-2}{-2}\) = 1
Slope of BC = \(\frac{1-(-4)}{7-2}=\frac{5}{5}\) = 1
Slopes are equal ∴ the points are collirear
![]()
Question 25.
Find the equation of the line through (1, 2) and making an angle of 60° with the positive direction of x-axis.
Answer:
Given = (1, 2) and θ = 60°
m = tan θ = tan 60° = \(\sqrt{3}\)
Required equation is y – y1 = m(x – x1)
y – 2 = \(\sqrt{3}\)(x – 1)
y – 2 = \(\sqrt{3}\)x – \(\sqrt{3}\)
⇒ \(\sqrt{3}\)x – y + 2 – \(\sqrt{3}\) = 0
PART-C
II. Answer any TEN questions: (10 × 3 = 30)
Question 26.
Find the greatest number which divides 98, 120, and 153 leaving the same remainder.
Answer:
We have to find the H.C.F of 120 – 98, 153 – 120, 153-98
Required is H.C.F of 22, 33, 55
∴ H.C.F is 11
Hence the greatest number is 11.
Question 27.
Show that the relation “Congruent to” on the set of all triangles is an equivalence relation.
Answer:
Every triangle is congruent to itself
∴ the relation is reflexive
∆T1 is congruent to ∆T2 ⇒ ∆T2 is congruent to ∆T1 ⇒ R is symmetric
If triangle T, is congruent to T2, ∆T2 is congruent to ∆T3 then ∆T1 is congruent to ∆T3
∴ the relative is transitive Hence the relation “congruent to” is an equivalence relation.
Question 28.
If A = {1, 3, 5}, B = {5, 7}, C = {7} verify that A ∪ (B ∩ C) – (A ∪ B) ∩ (A ∪ C)
Answer:
A ∪ (B ∩ C) = {1, 3, 5} ∪ {7} = {1, 3, 5, 7}
(A ∩ B) ∩ (A ∪ C) = {1, 3, 5, 7} ∩ {1, 3, 5, 7} = {1, 3, 5, 7}
Question 29.
If px = qy = rz = sw and pq = rs then prove that \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}+\frac{1}{w}\)
Answer:
Let px = qy = rz = sw = k
⇒ p = k1/w, q = k1/y, r = k1/z, s = k1/w
Also given pq = rs
⇒ k1/xk1/y= k1/zk1/w
⇒ k1/x+1/y = k1/z+1/w
⇒ \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}+\frac{1}{w}\)
Question 30.
Find the nature of roots of the equation 3x2 + 2x + 1 = 0 without solving. If α and β are the roots of 3x2 + 2x + 1 = 0 find the value of \(\).
Answer:
Δ = b2 – 4ac = 4 – 12 = -8 < 0 ∴ the roots are imaginary
α + β = \(\frac{-b}{a}=\frac{-2}{3}\) & α.β = \(\frac{c}{a}=\frac{1}{3}\)
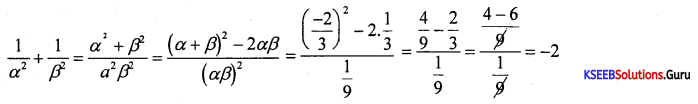
![]()
Question 31.
The sum of four numbers which are in A.P. is 28 and 10 times the least numbers is 4 times the greatest. Find the numbers.
Answer:
Let the 4 numbers are a – 3d, a-d, a+d, a+3d
Given sum = 28
![]()
4a – 28 ⇒ a = 1
Also given 10(a – 3d) – 4(a + 3d)
10a – 30d = 4a + 12d
6a = 42 d
42 = 42d ⇒ d = 1
∴ the 4 numbers are 4, 6,8,10
Question 32.
Solve the linear inequalities x + 3y ≤ 3 2x + y, 2, x,y ≥ 0 graphically.
Answer:
Consider x + 3y = 3 .
If x = 0, then y = 1 (0,1)
If y = 0 then x = 3 (3, 0)
2x + y – 2
If x = 0, y = 2 (0, 2)
If y = 0 then x = 1, (1, 0)
Plot the two lines on the graph there
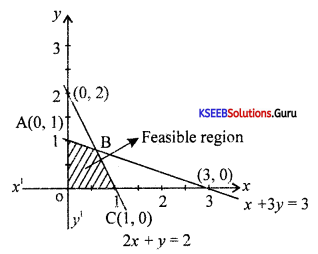
Question 33.
XYZ suppliers buy a machine for Rs. 20,000 the rate of depreciation is 10%. Find the depreciated value of the machine after 3 years. Also, find the amount of depreciation.
Answer:
B = C (1 – r)n
Given C = 20,000, r = 0.1, n = 3 B = ?
B = 20,000 (1~0.1)3 = ₹ 14,580
the amount of depreciation = 14,580 ₹
![]()
Question 34.
The average age of A and B is 18 years, the average age of B and C is 17 years and that of C and A is 20 years. Find A’s age.
Answer:
Given a + b = 36 – 0 → (1)
b + c = 34 (2) → (2)
c + a = 40 → (3)
Adding we get 2{a + 6 + c) = 110 ⇒ a + b + c = 55 → (4)
Equ 4 – Equ 2 gives a = 55 – 34 = 21
Where A’s age = a = 21 yrs
Question 35.
A certain amount invested at 4% p.a. compounded semi-annually amount to Rs. 78030 at the end of one year. Find the sum.
Answer:
F = 78,030, r = 4% = 0.04, n = 1 yr
F = P\(\left(1+\frac{r}{2}\right)^{n \times 2}\)
78,030 = P\(\left(1+\frac{0.02}{2}\right)^{2}\)
P = \(\frac{78.030}{(1.01)^{2}}\) = ₹75,000
Question 36.
Prove that \(\sqrt{\frac{\sec \theta+1}{\sec \theta-1}}=\frac{1+\cos \theta}{\sin \theta}\)
Answer:
L.H.S = \(\sqrt{\frac{\sec \theta+1}{\sec \theta-1}} \times \frac{\sqrt{\sec \theta+1}}{\sqrt{\sec \theta+1}}\)
\(\frac{(\sqrt{\sec \theta+1})^{2}}{\sqrt{\sec ^{2} \theta-1}}=\frac{\sec \theta+1}{\tan \theta}=\frac{\frac{1}{\cos \theta}+1}{\frac{\sin \theta}{\cos \theta}}=\frac{1+\cos \theta}{\sin \theta}\) = R.H.S
Question 37.
Derive slope-intercept form of line y = mx + c. Also, write the equation of passing through origin with slope m.
Answer:
Let the line passess thr y-axis at A(0, C) and x-axis at B, and m = tanθ is slope of the line by using one point formula we get y – y1 = m(x – x1)
y – c = m(x – 0)
⇒ y – c – mx
⇒ y = mx + c is the required equation of the line.
Also equation passing thr (0, 0) is y = mx
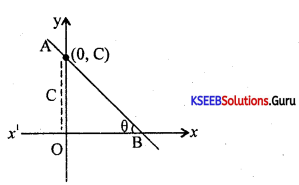
Question 38.
Find the equation of the line which passes through the point (-4, 5) and whose intercepts are equal in magnitude but opposite in sign.
Answer:
Intercept form is \(\frac{x}{a}+\frac{y}{b}\) = 1
Given b = -a
∴ \(\frac{x}{a}+\frac{y}{-a}\) – 1
of x – y = a
This equn passess through (-4, 5)
-4 – 5 = a ⇒ a = – 9
∴ The required equation is x – y = 9
PART-D
IV. Answer any SIX questions: (6 × 5 = 30)
Question 39.
In a college, 2/5th of the students play basketball, and 3/4th play volleyball. If 50 students play none of these two games and 125 play both find the numbers of students who play.
(a) at least one of the two games.
(b) exactly one
Represent the results using the Venn diagram.
Answer:
Let total students = x,
Let A = basket ball and B = volley ball
∴ n(A) = \(\frac{2}{5}\)x
n(B) = \(\frac{3}{4}\)x
Given n (AUB)’ = 50 n(AnB) = 125
n(AUB) = x – x(AUB)’ = x – 50
(a) n(AuB) = n(A) + n(B) – n(A n B)
x – 50 = 0.4x + 0.75x – 125
∴ 75 = 1.15x – 1x = 0.15x
x = \(\frac{75}{0.15}\) = 500
n( A u B) = x – 50 = 500 – 50 = 450
(b) n(only A) + n(only B)
n(A) = \(\frac{2}{5}\) × 500 = 200
= 200 – 125 + 375 – 125
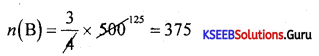
= 325
Question 40.
Evaluate \(\frac{1.234 \times .0 .8921}{43.43 \times 0.0092}\) using logarithm table.
Answer:
Let x = \(\frac{1.234 \times .0 .8921}{43.43 \times 0.0092}\)
Taking logm both sides we get
logx = log 1.234 + log 0.8921 – log43.43 – log 0.0092
= 0.931 + 1.9504 – 1.6378 – 3.9638
logx = 0.4401
x = A.L(0.440l)
x = 2.755.
Question 41.
Ms. Sneha buys a second-hand bike for Rs. 18,000 she pays Rs. 12,000 cash and agrees to pay the balance in 12 annual installments of Rs. 500 each plus 10% interest on the unpaid amount. How much will the bike cost her?
Answer:
Balance amount 18,000 – 12,000 = 6,000 Rs.
No. of instalment = 12, Each unit amt = Rs. 500
1st instalment = 500 + 6000 × 0.1 = 1,100
2nd instalment = 500 + 5000 × 0.l = 1050
3rd instalment = 500 + 5000 × o. 1 = 1000
Cost of instalments = 1,100 + 1050 + 1000 +……………. 12 instalment
The terms are in A.P with d = -50, a = 1,100
∴ Sm = \(\frac{12}{2}\)[1,100 + (12-1) × -50] = 6(1,100 – 550) = 6 × 550 = ₹3300
∴ Total cost= 12,000 +3,300 = ₹15,300
![]()
Question 42.
Obtain a root of the equation x3 – 2x2 -2x + 3- 0 by inspection and then solve using synthetic division method.
Answer:
f(x) = x3 – 2x2 – 2x + 3
f(1) = 0 ∴ 1 is a root
∴ by sythetic division we have
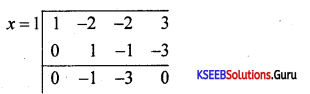
∴ Reduced equation is x2 – x – 3 = 0
∴ Roots are x = \(\frac{1 \pm \sqrt{13}}{2}\)
Hence the 3 roots are 1, \(\frac{1+\sqrt{13}}{2}\), \(\frac{1-\sqrt{13}}{2}\)
Question 43.
A person spent 30% of his wealth and thereafter ₹ 20,000 and a further 10% of the remainder. If 29,250 is still remaining, what was his total wealth amount?
Answer:
Let total wealth be Rs. x
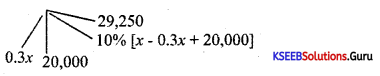
0.63x = 18,000
x = ₹ 75,000
Question 44.
A father wants to send his child for higher studies after 15 years. He expects the cost of higher studies to be Rs. 1,00,000. How much should he share annually to have one lakh after 15 years if the interest rate ¡s 12% C.I. per annum?
Answer:
Given data F = 1,00000, a = ?, n = 15, r = 0.12
F = \(\frac{a\left[(1+i)^{n}-1\right]}{i}\)
1,00,000 = a\(\frac{\left[(1+0.12)^{15}-1\right]}{0.12}\)
a = \(\frac{1,00000}{(1.12)^{75}-1}\) = ₹ 2682.47
Question 45.
Find x if \(\frac{x \sin ^{2} 300^{\circ} \cdot \sec 240^{\circ}}{\cos ^{2} 225^{\circ} \cdot {cosec} 240^{\circ}}\) = cot 135° tan 315°
Answer:
sin 300 = sin (360 – 60) = – sin 60 = \(\frac{\sqrt{3}}{2}\)
sec 240 = sec(180 + 60)= – sec60°= – 2
cos 225 = cos(180 + 45°) – cos45°= – \(\frac{1}{\sqrt{2}}\)
cosec 240 = cosec (180 + 60°) = – cosec 60 = – \(\frac{2}{\sqrt{3}}\)
cot 315° = cot (360 – 45°) = – cot 45° = – 1
tan 300 = tan (360 – 60°) = – tan 600 = – \(\sqrt{3}\)
∴ The given equation becomes:
\(\frac{x \cdot \frac{3}{4} \cdot 4}{\frac{1}{2}, \frac{4}{3}}\) = 1.3
⇒ x = \(\frac{6}{9}=\frac{2}{3}\)
![]()
Question 46.
In what ratio is the line segment joining the points (4, 5) and (1, 2) is divided by the x-axis. Also, find the coordinates of the point of division.
Answer:
Point on x-axis is y = 0
Let P(x, y) divide AB in
the ratio k: 1 ratio
∴ P(x, y) = \(\left(\frac{4 k+1}{k+1}, \frac{5 k+2}{k+1}\right)\)
(x, 0) = \(\left(\frac{4 k+1}{k+1}, \frac{5 k+2}{k+1}\right)\)
⇒ \(\frac{5 k+2}{k+1}\) = 0 ⇒ k = \(\frac{-2}{5}\)
ratio is 2: 5 externaily
∴ P = (-1, 0)
Question 47.
Find the equation for the locus of a point that moves such that the sum of its distances from (0, 3) and (0, -3) is 8 units.
Answer:
Let P(x, y)be a moving point
Given |PA| + |PB| = 8
|PA| = \(\sqrt{x^{2}+(y-3)^{2}}\) & |PB| = \(\sqrt{x^{2}+(y+3)^{2}}\)
|PA| = 8 – |PB|
S.B.S We get
x2 + (y – 3)2 = \(\left(8-\sqrt{x^{4}+(y+3)^{2}}\right)^{2}\)
Simplifying we get the required equation of the locus 16x2 + 7y2 = 112.
Question 48.
Show that the points (2, -2), (8, 4), (5, 7), and (-1, 1) are taken murder the vertices of a rectangle.
Answer:
AB = \(\)
Similarly BC = \(\sqrt{18}\) , CD = \(\sqrt{72}\) , DA = \(\sqrt{18}\) , AC = BD = \(\sqrt{90}\)
Opposite sides are equal and diagonals are equal
PART-E
V. Answer any ONE question : (6 × 5 = 30)
Question 49.
(a) If x = a r sin A cos B, y = br sin A sin B, z = cr cos A, prove that \(\)
Answer:
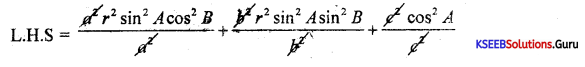
= r2[sin2 A(cos2B + sin2B) + cos2A] = r2 (sin2 A + cos2 A)
= r2 = RHS.
(b) Prove that the lines x + y + 4 = 0, 2x = 3y + 7 and 3x + y = -6 are concurrent. Also find the point of concerrency.
Answer:
Solving equations 1 and 2 we get
x + y + 4 = 0 …(1)
2x – 3y – 7 = 0 …(2)
x = -1 & y = -3
Put x = -1 and y = -3 in eqn (3) We get
3x + y = -6
3(-1) + -3 = -6 – 6 = – 6
Hence the 3 lines are concurrent and the point of concurrency (-1, -3)
(c) Find the present value of a perpetuity of Rs. 3000 to be received forever at 4 p.a.
Answer:
Given A = 3000, r = 0.04, P∞ = ?
P∞ = \(\frac{A}{r}=\frac{3000}{0.04}\) = 75,000
∴ Present value of perpetuity = 75,000
![]()
Question 50.
(a) Find the sura of all numbers between 50 and 200 which are divisible by 11.
Answer:
Numbers are 55, 66, 77, ……………….. 198
which are in A.P
Here a = 55, Tn = 198, d= 11
198 = 55 + (n – 1)11
n = 14
∴ Sn = \(\frac{14}{2}\)(55 + 198) = 1771
(b) A company sells ‘x’ tins of talcum powder per day at Rs. 10/tin. The cost of manufacturing a tin is Rs. 6 and distributor charge per tin is Rs. 1. Besides, the daily overhead cost is Rs. 600. Determine
(i) Cost function
(ii) Revenue function
(iii) Profit function
(iv) Break even level of production.
Answer:
(i) C(x) =V.C + E.C
= 6x + x + 600
∴ C(x) = 7x + 600
(ii) R(x) = Price x Quantity
R(x) = 10x
(iii) P(x) = R(x) – C(x)
= 10x – 7x – 600
P(x) = 3x – 600
(iv) At BEP:P(x) = 0 or R(x) = C(x)
3x – 600 = 0
x = 200 units
∴ Break even level of production 200 units
(c) Form the LCM of 2/3, 4/5, 6/7
Answer:
LCM of fractions = \(\frac{\text { LCM of NR }}{\text { HCF of DNR }}=\frac{\text { LCM of } 2,4,6}{\text { HCF of } 3,5,7}=\frac{12}{1}\) = 12