1st PUC Basic Maths Previous Year Question Paper March 2018 (South)

Students can Download 1st PUC Basic Maths Previous Year Question Paper March 2018 (South), Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.

Karnataka 1st PUC Basic Maths Previous Year Question Paper March 2018 (South)

Time: 3.15 Hours
Max. Marks: 100

Instructions:

1. The questions paper consists of five parts A, B, C, D, and E.
2. Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
3. Write the question numbers properly as indicated in the questions paper

PART-A

I. Answer any TEN questions. (10 × 1 = 10)

Question 1.
Write the conjugate of 2 – i3.
Answer:
2 + i3

Question 2.
If A = {5,6}, Find power set of A.
Answer:
P(A) ={Φ, {5}, {5,6}, {6}}

Question 3.
Simplify \(\left[\left\{\sqrt[3]{x^{2}}\right\}^{3}\right]^{\frac{1}{2}}\)
Answer:
x

Question 4.
Express log₅ 0.2 = -1 in exponential form
Answer:
5^-1 = 0.2

Question 5.
Find the 8lh term of an AP -2, -4, -6 ………….
Answer:
T₈ = -2 + 7 (-2) = -2 – 14 = -16

Question 6.
Solve for x : 2(1+x) – 10 = 16 – 2 (x – 24).
Answer:
14 + 2x- 10 = 16 – 2x + 48 ⇒ x = 15

Question 7.
Find the simple interest on ₹ 1500 at 4% p.a for 145 days.
Answer:
SI = \(\frac{\mathrm{P} t r}{100}\) = 23.84

Question 8.
Define Annuity.
Answer:
An annuity is a fixed sum of money paid at regular intervals of time under certain conditions.

Question 9.
Convert 42% to a decimal.
Answer:
\(\frac{42}{100}\) = 0.42

Question 10.
Convert \(\frac{3 \pi^{c}}{2}\) into degree measure.
Answer:
\(\frac{3 \pi}{2} \times \frac{180}{\pi}\) = 270

Question 11.
Prove that Sin 30°. Cos 60° + cos 30°. Sin 60° = 1
Answer:
\(\frac{1}{2} \times \frac{1}{2}+\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}=\frac{1}{4}+\frac{3}{4}\) = 1

Question 12.
Find the slope of the line with the inclination \(\frac{\pi}{4}\) with respect to x – axis
Answer:
θ = π/4 ⇒ m = tanπ/4 = 1

Part – B

II. Answer any TEN questions. (10 × 2 = 20)

Question 13.
Find the LCM of 36, 40, and 48 by the factorization method.
Answer:
36 = 2² × 3², 40 = 2³ × 5¹, 48 = 2³ × 3¹
LCM = 2⁴ × 3² × 5¹ = 720

Question 14.
Find the number of positive divisors of 768.
Answer:

768 = 2⁸ × 3¹

Question 15.
If A = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7} and U = {1, 2, 3, 4, 5, 6, 7, 8, 9} verify (AuB)’ = A’∩B’
Answer:
(A∪B)1 = U – (A∪B) = {8,9}
A’ = {6, 7, 8, 9} B’ = {1,2, 8,9}
∴ A’∩B1 = {8, 9} (A∪B)’ = A’∩B’

Question 16.
Prove that (x^b-c)^a .(x^c-a)^b (x^a-b)^c = 1
Answer:
(x^b-c)^a .(x^c-a)^b (x^a-b)^c ⇒ x^{ab-ac+bc-ca-cb} ⇒x° = 1

Question 17.
The third term of a HP is \(\frac{1}{7}\) and Fifth term is \(\frac{1}{11}\) then find the seventh term.
Answer:
3rdterm of an A.P = 7 a + 2d = 7
5th term of A.P = 11 a + 4d = 11 ∴ a = 3 d = 2
seventh term of HP = \(\frac{1}{a+(n-1) d}\) = \(\frac{1}{3+6(2)}\) = 15

Question 18.
The sum of four consecutive numbers is 366, find them.
Answer:
x + x + 1 + x + 2 + x + 3 = 366
⇒ x = 90 numbers are 90, 91, 92, 93

Question 19.
Solve x² + 3x – 28 = 0 by formula method.
Answer:
x = \(\frac{3 \pm \sqrt{9-4(1)(-28)}}{2}\) ⇒ x = -4 or x = 7

Question 20.
Solve : 5x – 3 > 3x + 1 ; xeR and represent on the number line.
Answer:
5x – 3 < 3x + 1 ⇒ 2x < 4 ⇒ x < 2

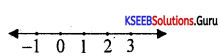
Question 21.
Find the present value of an annuity of ₹400 for 3 years at 16% p.a compound interest
Answer:
P = \(\frac{400\left[(1+0.16)^{3}-1\right]}{0.16(1+0.16)^{3}}\) = 898.35

Question 22.
The angles of a triangle are in the ratio 3:4:5. Find them in degrees.
Answer:
3A + 4A + 5A = 180 ⇒ A= 15 45°, 60°, 75°

Question 23.
Prove that Sin (480°).cos (690°) + cos (780°). Sin (1050°) = 1/2
Answer:
sin (360 + 120) = sin 120 = sin (180 – 60 = sin 60 = \(\frac{\sqrt{3}}{2}\)
cos (720 – 30) = cos 30 = \(\frac{\sqrt{3}}{2}\) cos (720 + 60) = cos 60 = \(\frac{1}{2}\)
sin (1080 – 30) = sin (-30) = -1/2 .
\((\sqrt{3} / 2)(\sqrt{3} / 2)-(1 / 2)(1 / 2)=3 / 4-1 / 4=2 / 4=1 / 2\)

Question 24.
Show that the points (1,1), (5,2) and (9,5) are collinear.
Answer:
AB = 5 BC = 5 AC =10
∴ AB + BC = AC
5 + 5 = 10

Question 25.
Find the equation of the locus of a point that moves such that the square of its distance from (2,3) is 3.
Answer:
Let p (x, y) be any point on the locus PA² = 3
(x – 2)² + (y – 3)² = 3 ⇒ x² + y² – 4x – by +10 = 0

Part – C

III. Answer any TEN questions. (10 × 3 = 30)

Question 26.
Prove that \(\sqrt{2}\) is an irrational number.
Answer:
We shall prove it by the method ofcontradiction.
If possible Let \(\sqrt{2}\) be a rational number
Let \(\sqrt{2}\) = \(\frac{p}{q}\) where p and q are Integers and q ≠ 0.
Further let p and q are coprime i.e. H.C.F. of p and q = 1.
\(\sqrt{2}\) = \(\frac{p}{q}\) ⇒ \(\sqrt{2}\)q = p
⇒ 2q² = p²
⇒ 2 divides p² ⇒ 2 divides p
⇒ p is even
Let p = 2k where k is an integer p² = 4k²
2q² = 4k²
q² = 2k² ⇒ q² is even
⇒ q is even.
Now p is even and q is even which implies p and q have a common factor 2. which is a
contradiction of the fact that p and q are co-prime.
∴ our assumption that \(\sqrt{2}\) is rational is wrong and hence \(\sqrt{2}\) is irrational.

Question 27.
Let f = {(1, 1), (2, 3), (0, -1)} be a function from z to z defined by f(x) = ax + b some integers a and b. Determine a and b.
Answer:
f(x) = ax + b
when x = 1 f(x) = 1
∴ a + b = 1
x = 0 f(x) = -1
a(0) + b – 1 ⇒ b = -1
a + b = 1
a – 1 = 1 ⇒ a = 1 + 1 =2
∴ a = 2
∴ a = 2, b = 1

Question 28.
If ax = by = cz and b2 = ac. Show that \(\frac{1}{x}+\frac{1}{z}=\frac{2}{y}\)
Answer:
Let a^x = b^y = c^z = k (say)
∴ a^x = k ⇒ a = k^1/x, b^y = k ⇒ b = k^1/y, c^z = k ⇒ c = k^1/z
Now, b² = ac
∴ (k^1/y)² = k^1/x. k^1/z
∴ k^2/y = k^1/x+1/z
Bases are the same ∴ Equating powers on both sides, we get.
\(\frac{1}{x}+\frac{1}{z}=\frac{2}{y}\)

Question 29.
Prove that \(\frac{1}{\log _{2} 4}+\frac{1}{\log _{8} 4}+\frac{1}{\log _{16} 4}\) = 4
Answer:
LHS = \(\frac{1}{\log _{2} 4}+\frac{1}{\log _{8} 4}+\frac{1}{\log _{16} 4}\) = log₄2 + log₄8 + log₄ 16
= log₄2.8. 16 = log₄ 256 = log₄ 4⁴ = 4log₄4 = 4(1) = 4 = RHS

Question 30.
Find the three numbers in GP whose sum is \(\frac{31}{5}\) and their product is 1.
Answer:
Let the number \(\frac{a}{r}\), a, ar
Product of extremes = 1
\(\frac{a}{r}\) × ar =1 ⇒ a² = 1 ⇒ a= 1
Sum \(\frac{13}{3} \Rightarrow \frac{a}{r}\) + a + ar = \(\frac{13}{3} \Rightarrow \frac{1}{r}\) + 1 + (1)r = \(\frac{13}{3}\)
\(\frac{1}{r}\) + r = \(\frac{13}{3}\) – 1
\(\frac{1+r^{2}}{r}=\frac{10}{3}\)
⇒ 3 + 3r² = 10r³⇒ 3r² – 10r + 30 = 3r² – 9r – r + 3O
⇒ 3r(r – 3) – 1 (r – 3) = 0
(r – 3)(3r – 1) = 0 ⇒ r = 3 or r = \(\frac{1}{3}\)
The numbers are
\(\frac{a}{r}\), a, ar
\(\frac{1}{3}\), 1, 1.3
⇒ \(\frac{1}{3}\), 1, 3

Question 31.
If a and P are the roots of the equation 2x² + 5x + 5 = 0, find the value of \(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}\)
Answer:

Question 32.
Solve the linear inequalities x + 2y ≤ 8, 2x + y ≤ 8, u ≥ 0, x ≥ 0 graphically.
Answer:

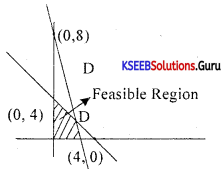
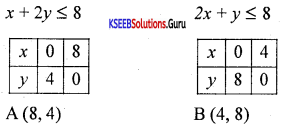
Question 33.
In how many years a sum of ₹2000 becomes ₹2205 at the rate of 5% p.a compound interest?
Answer:
A = (1 + r)ⁿ
n = \(\frac{\log A-\log p}{\log (1+r)}=\frac{3.3434-3.3010}{0.0211}\) = 2 years.
Future value = 4,575.9

Question 34.
The average weight of a group containing 25 persons is 70 kg. 5 persons with an average weight of 63kg leave the group and 4 persons with a weight of 72 kg, 78 kg, 70 kg, and 73 kg joins the group. Find the average weight of the new group.
Answer:
Average weight of 25 persons 70 kg
Total weight of 25 persons = 25 × 70 = 1750kg
Average weight of 5 persons who leave the group = 63 kg
∴ Total weight of 5 persons who leave the group 63 x 5 = 315kg

Total weight of4 persons who join the group = 72 + 78 + 70 + 73 = 293kg
∴ Total weight of the group now containing 24 persons = 1750 – 315 + 293 = 1728kg
∴ Average weight of the group now = \(\frac{1728}{24}\) = 72 kg

Question 35.
Savitha sold her bag at a loss of 7%. Had she been able to sell it at a gain of 9%, it would have fetched ₹ 64 more than it did. What was the cost price of the bag?
Answer:
Let CP = 100
loss at 7% ⇒ SP = 93 Gain at 9% ⇒ SP = 109 Difference 109 – 93 = 16
C.P of the bag = \(\frac{100 \times 64}{16}\) = ₹400

Question 36.
If sinθ = \(\frac{-8}{17}\) and π < θ < \(\frac{3 \pi}{2}\). Find the value of \(\frac{\tan \theta-\cot \theta}{\sec \theta+\operatorname{cosec} \theta}\)
Answer:
tan θ = 8/15, cot θ = 15/8
secθ = -17/5, cosec θ = 17/8
\(\frac{\tan \theta-\cot \theta}{\sec \theta-\cos e c \theta}=\frac{8 / 15-15 / 8}{-17 / 5-17 / 8}=\frac{171}{391}=\frac{7}{17}\)

Question 37.
Find the third vertex of a triangle if two of its vertices are at (-2, 4) and (7, -3) and the centroid at (3, -2).
Answer:
A (-2, 4) B = (7, -3) C = (x,, y) G = (3, -2) (3, – 2) = \(\left(\frac{-2+7+x}{3}, \frac{4-3+y}{3}\right)\)
⇒ x = 4, y = -7 ∴ C = (4,-7)

Question 38.
If the lines 2x – y = 5, Kx – y = 6 and 4x – y = 7 are concurrent, find K.
Answer:
2x – y – 5 = 0
4x – y – 7 = 0
Solving we get x = 1, y = -3
kx – y – 6 = 0 k( 1 ) – (-3) -6 = 0 ⇒ K = 3

Part – D

IV. Answer any SIX questions. (6 × 5 = 30)

Question 39.
Out of 250 people, 160 drink coffee, 90 drink tea, 85 drink milk, 45 drink coffee and tea, 35 drink tea and milk, 20 drink all three, i) How many will drink coffee and milk? ii) only milk iii) only coffee. Show the result through the Venn diagram.
Answer:
n(C∪T∪M) = 250
n(C) = 160,
n(T) = 90
n(M) = 85
n(C∩T)=45
n(T∩M) = 35
T(C∩T∩M)=20
n(C∩M)=?
n(C∪T∪M) = n(c) + n(T) + n(M) – n(C∩T) – n(T∩M) – n(M∩C)+ n(C∩T∩M)
250 = 160 + 90 + 85 – 45 – 35 – n(C∩M) + 20
∴ n(C∩M) = 160 + 90 + 85 – 45 – 35 + 20 – 250
∴ n(C∩M) = 25

Question 40.
Using logarthamic tables, find the value of \(\frac{0.5634 \times 0.0635}{2.563 \times 12.5}\)
Answer:
x = \(\frac{0.5634 \times 0.0635}{2.563 \times 12.5}\)
logx = log 0.5634 + log 0.0635 – log 2.563
-log 12.5 =1.7508 + 2.8028-0.4087-1.0969
= -2.952 = -2-1+1-0.952 = -3 + 0.048 = 3.0.048
x = AL[3.048] = 0.001117

Question 41.
Find the sum of all numbers between 50 and 200 which are divisible by 11.
Answer:
S_n = 55 + 66 + 77 +………….+ 198
a = 55
d = 11
T = 198
S_n = \(\frac{n}{2}\)[2 a + (n-1 )d] = 7(253) = 1771

Question 42.
Find an integral root between -3 and 3 by inspection and then using synthetic division solve the equation x3 – 10x² + 29x – 20 = 0
Answer:
Put x = I
1 – 10(1)² + 29(1) – 20
1 – 10 + 29 – 20
30 – 30 = 0

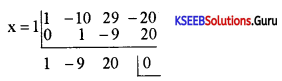
Quotient x² – 9x + 20
Remainder = 0
x³ – 10x² + 29x – 200
(x + 1)(x² – 9x + 20) = 0
x = -1, x² – 9x + 20 = 0
x = 4, x = 5

Question 43.
A person borrows a certain sum of money at 3% p.a Simple interest and invests the same at 5% p.a compound interest compounded annually. After 3 years he makes a profit of 1,082. Find the amount he borrowed.
Answer:
Let the amount invested be x
r =4% p.a.
A= 1352
p = x
n = 2
A = P (1 + r)ⁿ
1352 = x(1 + 0.04)² = x (1,04)² = x (1.0816)
∴ x = \(\frac{1352}{1.0816}\) = 1,250
∴ Amount invested Principal = 1,250
P = 1250 T = 2 r = 4%
ST = \(\frac{\mathrm{P} \times \mathrm{T} \times \mathrm{R}}{100}=\frac{1250 \times 2 \times 4}{100}\) = 100
A = P + SI = 1250 + 100 = 1350
If the same amount at the same rate of simple interest then
1352 – 1350 = Rs. 2 less will be received.

Question 44.
If Poornima deposits ‘600 at the beginning of every year for the next 15 years. Then how much will be accumulated at the end of 15 years, if the interest rate is 7% p.a?
Answer:
a = 600
n = 15
i = 0.07
F =a\(\frac{\left[(1+i)^{n}-1\right]}{i}\)(1 + i) = \(\frac{600\left[(1.07)^{15}-1\right]}{0.07}\)(1 + 0.07) = ₹ 161325.428.

Question 45.
A businessman sells an article for ₹ 720 and earns a profit of 20% Find the a) cost price b) profit percentage at the selling price.
Answer:
SP = Rs.720 profit = 20%
CP = SP × \(\frac{100}{(100+\text { Profit } \%)}\) = 720 × \(\frac{100}{(100+20)}\) = 720 × \(\frac{100}{120}\) = Rs. 600
Profit = SP – CP = 720 – 600 = Rs. 120
Profit percentage at selling price = \(\frac{\text { Profit }}{\mathrm{SP}}\) × 100 = \(\frac{120}{720}\) × 100 = 16.6%

Question 46.
If x = r cos A.cos B, y = r cos A. sin B and z = r sin A. then prove that x² + y² + z² = r²
Answer:
LHS = x² + y² + z² = r²cos²Acos²B + r²cos²Asin²B + r²sin²A = r²cos²A(cos²B + sin²B) + rsin²A = r²cos²A(1) + rsin²A = r²(cos²A + sin²A) = r²(1) = r² = RHS

Question 47.
Find the coordinates of the vertices of the triangle given the mid points of the sides as (4, -1), (7, 9) and (4, 11)
Answer:
Let A = (x₁, y₁) B = (x₂, y₂) and C = (x₃, y₃)

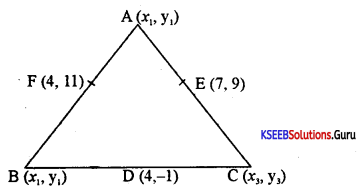
Now D = midpoint of BC .
= (4, -1) = \(\left[\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right]\)
x₂ + x₃ = 8 …………….(1)
y₂ + y₃ = -2 …………(2)

E = mid point of CA
(7, 9) = \(\left(\frac{x_{3}+x_{1}}{2}, \frac{y_{3}+y_{1}}{2}\right)\)
x₃ + x₁ = 14 …………(3)
y₃ + y₁ = 18 ………….(4)

F = mid point of AB
(4, 11) = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
x₁ + x₂ = 8 …………. (5)
y₁ + y₂ = 22 ………….(6)

Solving (1), (3), (5) we get x₁, x₂ and x₃
Consider (1) + (3) + (5) we get
2(x₁ + x₂ + x₃) = 30
(x₁ + x₂ + x₃) = 15
x₁ + x₂ = 8 and x₁ + x₂ + x₃ = 15 ⇒ x₃ = 7
x₂ + x₃ = 8 and x₁ + x₂ + x₃ = 15 ⇒ x₁ = 7
x₃ + x₁ = 14 and x₁ + x₂ +x₃ = 15 ⇒ x₂ = 1
Consider (2) + (4) + (6) we get
2 (y₁ + y₂ + y₃) = 38
(y₁ + y₂ + y₃) = 19

Now y₂ + y₃ = – 2 and(y₁ + y₂ + y₃) = 19 ⇒ y1 =21
y₃ + y₁ = 18 and (y₁ + y₂ + y₃) = 19 ⇒ y₂ = 1
y₁ + y₂ = 22 and (y₁ + y₂ + y₃) = 19 ⇒ y₃ = 1
Thus A = (7, 21) B = (1, 1) and C = (7, -3)

Question 48.
Find the coordinate of the foot of the perpendicular from (-6, 2) on the line 3x – 4y + 1 = 0.
Answer:

Part-E

V. Answer any ONE question. (1 × 10 = 10)

Question 49.
(a) Find tue domain and Range of the function f(x) = \(\frac{x^{2}-2 x+1}{x^{2}-9 x+13}\) where x ∈ N
Answer:
Domain of F(x) = N{1, 2, 3…………… )
n = 1 ⇒ F(x) = \(\frac{1-2+1}{1-9+13}=\frac{0}{5}\) =0
n = 2 ⇒F(x) = \(\frac{4-4+1}{4-18+13}=\frac{1}{-1}\) = -1
n = 3 ⇒ F(x) = \(\frac{9-6+1}{9-27+13}=\frac{4}{-5}\)…………
Range of F(x) = {0, -1, \(\frac{4}{-5}\),………………}

(b) Find the distance between the parallel lines 5x + 12y + 7 0 and 5x + 12y – 19= 0
Answer:
d = \(\left|\frac{C_{1}-C_{2}}{\sqrt{a^{2}+b^{2}}}\right|=\left|\frac{26}{\sqrt{25+144}}\right|=\left|\frac{26}{\sqrt{169}}\right|=\frac{26}{13}\) = 2 units

(c) What is the present value of an income of 3000 to be received forever if the interest rate is 14% p.a.
Answer:
P_∞ = \(\frac{a}{i}=\frac{3000}{0.14}\) = 21428.5

Question 50.
(a) Find the sum of n terms of the series 7 + 77 + 777 + …… n terms.
Answer:

(b) A confectioner makes and sells biscuits. He sells one pack of biscuits at ₹ 80 His cost of manufacturings is ₹40 pack as variable cost and ₹ 3000 a fixed cost find i) Revenue function ii) Cost function iii) Profit function iv) If he limits his production to 100 packets can. he makes a profit.
Answer:
Revenue function (i) R (X) = 80.x TC = TVC + TFC
(ii) C(x) = ax + b = 40.x + 3000
(iii) P(x) = R(.x) – C(x) = 80 x – (40 x + 3000) = 80x – 40x – 3000 = 40.x – 3000
(iv) x= 100
P(x) = 40x-3000 P(100) = 4(100) -3000 = ₹1000

(c) The profit of a business firm for the 5 years are ₹17,598, ₹20,703, ₹10,085, ₹25,375, and ₹16,315. Find the average profit?
Answer:
Average profit = \(\frac{17598+20703+15085+25375+16315}{5}\) = ₹19015.20