1st PUC Basic Maths Previous Year Question Paper March 2019 (South)

Students can Download 1st PUC Basic Maths Previous Year Question Paper March 2019 (South), Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.

Karnataka 1st PUC Basic Maths Previous Year Question Paper March 2019 (South)

Time: 3.15 Hours
Max. Marks: 100

Instructions:

1. The questions paper consists of five parts A, B, C, D, and E.
2. Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
3. Write the question numbers properly as indicated in the questions paper

PART-A

I. Answer any TEN questions. (10 × 1 = 10)

Question 1.
Define a prime number
Answer:
Numbers which are divisible by one and the number itself is called prime number. {2,3,5,7,11,…………}

Question 2.
If A = {a, b, c, d}, B = {d, e, f, g}, find A-B.
Answer:
A – B = {a, b, c}

Question 3.
Simplify \(\left\{\frac{5 x^{3}}{y}\right\}^{2}\)
Answer:
\(\frac{25 x^{6}}{y^{2}}\)

Question 4.
Find x if log_x625 = 4.
Answer:
x⁴ = 625 ⇒ x⁴ = 5⁴ ⇒ x = 5.

Question 5.
Find the 11“’ term of the AP 3, 5, 7, 9
Answer:
T₁₁ = 3 + (11 – 1)2 ⇒ T_n = 3 + 20 = 23.

Question 6.
Solve for x if (x + 2) (x + 3) = (x – 2) (x – 4).
Answer:
x² + 6 + 5x = x² + 8 – 6x
11x = 2 ⇒ x = \(\frac{2}{11}\)

Question 7.
Find the simple interest on ₹ 600 for 3 years at 4% p.a.
Answer:
SI = \(\frac{600 \times 3 \times 4}{100}\) = ₹ 72

Question 8.
Find the present value of a perpetuity of ₹ 3000 to be received forever at 4% p.a.
Answer:
A = Rs, 3000
r = 0.04
P∞ = \(\frac{\mathrm{A}}{\mathrm{r}}=\frac{3000}{0.04}\) = 75000

Question 9.
Convert \(\frac{1}{4}\) into percentage.
Answer:
\(\frac{1}{4}\) × 100 = 25%

Question 10.
Express \(\frac{3 \pi}{2}\) in degrees.
Answer:
\(\frac{3 \pi}{5}=\frac{3 \times 180}{5}\) = 108°

Question 11.
Find the value of sin²120 + cos²120.
Answer:
sin²120 + cos²120 = 1

Question 12.
Find the slope of line 2x + 3y – 11 = 0.
Answer:
5y = -2x + 11
y = \(\frac{-2}{5}\)x + \(\frac{11}{5}\) compare with y = mx + c
∴ m = slope = \(\frac{-2}{5}\)

Part – B

II. Answer any TEN questions. (10 × 2 = 20)

Question 13.
Find the number of divisors of 825.
Answer:
825 = 3¹ x 5² x 11¹
P₁ = 3, α₁ = 1,P₂ = 5, α₂ = 2, P₃ = 11, α₃ = 11
T (n) = (1 + α₁) (1 + α₂) (1 + α₃)
= (1+ 1)(1 +2)(1 + 1)
= (2)(3)(2)
= 12

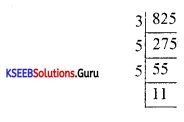
S(n) = \(\left(\frac{p_{1}^{\alpha_{1}+1}-1}{p_{1}-1}\right)\left(\frac{p_{2}^{a_{i}+1}-1}{p_{2}-1}\right)\left(\frac{p_{1}^{a_{1}+1}-1}{p_{3}-1}\right)\)
S(825) = \(\frac{3^{2}-1}{3-1} \times \frac{5^{3}-1}{5-1} \times \frac{11^{2}-1}{11-1}\)
= \(\frac{8}{2} \times \frac{124}{4} \times \frac{120}{10}\)
= 4 × 31 × 12 = 1488

Question 14.
Find the number which, when divided by 16, 20 and 40 leaves the same remainder 4.
Answer:
16 = 2⁴, 20 = 2² × 5¹, 40 = 2³ × 5¹
LCM = 2⁴ × 5¹ = 16 × 5 = 80
∴ Required number = 80 + 4 = 84.

Question 15.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6} and U = {1, 2-, 3, 4, 5, 6, 7, 8} verify (A∪B)’ = A’∩B’
Answer:

1200 = 2⁴ × 5² × 3¹ = p₁^α₁× p₂^α₂ × p₃^α₃
P₁ = 2 P₂ = 5; P₃ = 3 α₁ = 4; α₂ = 2; α₃ = 1
T(n) = (1 + α₁)(1 + α₂)(1 + α₃) = (1 + 4)(1 + 2)(1 + 1) = (5)(3)(2) = 30
S(n) = \(\left(\frac{\mathrm{P}_{1}^{\alpha_{1}+1}-1}{\mathrm{P}_{1}-1}\right)\left(\frac{\mathrm{P}_{2}^{\alpha_{2}+1}-1}{\mathrm{P}_{2}-1}\right)\left(\frac{\mathrm{P}_{3}^{\alpha_{3}+1}-1}{\mathrm{P}_{3}-1}\right)\)
= \(\left(\frac{2^{5}-1^{\circ}}{2-1}\right)\left(\frac{5^{3}-1}{5-1}\right)\left(\frac{3^{2}-1}{3-1}\right)=\left(\frac{31}{1}\right)\left(\frac{124}{4}\right)\left(\frac{8}{2}\right)\)
= 31 × 124 = 3844

Question 16.
Simplify \(\left[\frac{x^{a}}{x^{b}}\right]^{a+b}\left[\frac{x^{b}}{x^{c}}\right]^{b+c}\left[\frac{x^{c}}{x^{a}}\right]^{c+a}\)
Answer:

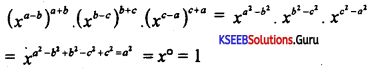
Question 17.
Which clement of the GP 5, 10, 20………. is 80.
Answer:
T_n = ar^n-1
80 = 5.2^x-1
2^n-1 = 16 ⇒ 2^n-1 = 2⁴ ⇒ n-1 = 4⇒ n = 5

Question 18.
The sum of the two numbers is 107 and their difference is 17. Find the numbers.
Answer:

∴ a = 62
a + b = 107
b = 107 – a = 107 – 62 = 45
∴ b = 45

Question 19.
Solve by formula method: 5x² – 7x – 12 = 0.
Answer:
x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{-(-7) \pm \sqrt{(-7)^{2}-4(5)(-12)}}{(2)(5)}\) ⇒ x = \(\frac{24}{10}\) and x = -1

Question 20.
Solve : 3x – 2 < 2x + 1 ; x∈ R and represent on the number line.
Answer:
3x – 2 < 2x + 1
3x – 2x < 2+ 1
x < 3

Question 21.
Find the future value of an annuity due of ₹ 800 for 3 years at 5% p.a.
Answer:
F = \(\frac{a\left[(1+i)^{n}-1\right]}{i}\)(1 + i) = \(\frac{800\left[(1+0.05)^{3}-1\right]}{(0.05)}\)(1 + 0.05)
F = ₹ 2287.14

Question 22.
Prove that tan²A(1 – sin2A) = sin2A.
Answer:
LHS = tan² A cos² A = \(\frac{\sin ^{2} A}{\cos ^{2} A}\)cos² A- = sin² A = RHS

Question 23.
Find the value of cot²60° + sin²45° + sin²30° + cos²90°.
Answer:
\(\left(\frac{1}{\sqrt{3}}\right)^{2}+\left(\frac{1}{\sqrt{2}}\right)^{2}+\left(\frac{1}{2}\right)^{2}\) + 0 = \(\frac{1}{3}+\frac{1}{2}+\frac{1}{4}=\frac{13}{12}\)

Question 24.
A point P moves such that PA² = 3PB². If A = (5, 0), B = (-5, 0). Find the equation of the locus of P.
Answer:
Let P(x, y) be the point on the locus
Given PA² = 3PB² and A = (5, 0), B (—5, 0)
(x – 5)² + (y – 0)² = 3[(x+ 5)² + (y – 0)²]
x² + 25 – 10x + y² = 3[x² + 25 + 10x + y²]
3x² + 75 + 30x + 3y² – x² + y² – 10x + 25
2x² + 2y² + 40x + 50 = 0 is the required equation.

Question 25.
If the distance between the points (3, -2) and (-1, a) is 5 units find the values of a.
Answer:
AB = \(\sqrt{(-1-3)^{2}+(a+2)^{2}}\) =5
Squaring and simplifying we get
a = 1 and a = -5

Part – C

III. Answer any TEN questions. (10 × 3 = 30)

Question 26.
Prove that \(\sqrt{2}\) is an irrational number.
Answer:
We shall prove it by the method ofcontradiction.
If possible Let \(\sqrt{2}\) be a rational number
Let \(\sqrt{2}\) = \(\frac{p}{q}\) where p and q are Integers and q ≠ 0.
Further let p and q are coprime i.e. H.C.F. of p and q = 1.
\(\sqrt{2}\) = \(\frac{p}{q}\) ⇒ \(\sqrt{2}\)q = p
⇒ 2q² = p²
⇒ 2 divides p² ⇒ 2 divides p
⇒ p is even
Let p = 2k where k is an integer p² = 4k²
2q² = 4k²
q² = 2k² ⇒ q² is even
⇒ q is even.
Now p is even and q is even which implies p and q have a common factor 2. which is a
contradiction of the fact that p and q are co-prime.
∴ our assumption that \(\sqrt{2}\) is rational is wrong and hence \(\sqrt{2}\) is irrational.

Question 27.
If f(x) = x + 1 and g(x) = x² + 1. Find (1) fog(1) (2) fog(2) (3) gof(2)
Answer:
(i) fog(1) =f(g(1))
= f(2)
= 2 + 1 = 3

(ii) fog (2) = f(g (2))
= f(5)
= 5 + 1 = 6

(iii) gof (1)
= gof (1)
= g(f(1))
= g (2) = 4 + 1 = 5

Question 28.
If a^x = b^y = c^z and b² = ac. Show that \(\frac{1}{x}+\frac{1}{z}=\frac{2}{y}\)
Answer:
Let a^x = b^y = c^z = k(say)
∴ a^x = k ⇒ a = k^1/x, b^y = k ⇒ b = k^1/y, c^z = k ⇒ c = k^1/z
Now, b² = ac
∴ (k^1/y)² = k^1/x. k^1/z
∴ k^2/y = k^1/x+1/z
Bases are the same ∴ Equatlig powers on both sides, we get.
\(\frac{2}{y}=\frac{1}{x}+\frac{1}{z}\)

Question 29.
Solve log x + log (x – 4) – log (x – 6) = 0
Answer:
logx(x-4) – log(x-6) = 0
⇒ log\(\) = 0 ⇒ \(\) = 1 ⇒ x² – 5x + 6 = 0
x = 2 or 3

Question 30.
Find the three numbers in GP whose sum is 39 and their product is 729.
Answer:
Let the three numbers be \(\frac{a}{r}\),a,ar
Product = 729
⇒ a³ = 729 ⇒ a³ = 9³ ⇒a = 9
Sum = 39
\(\frac{a}{r}\) + a + ar = 39
\(\frac{9}{r}\) + 9 + 9r = 39
\(\frac{9}{r}\) + 9r = 39 – 9
\(\frac{9}{r}\) + 9r = 30
⇒ 9 + 9r² = 30
r ⇒ 9r² – 30r + 90
⇒ 9r² – 27r – 3r + 90
9r(r – 3)-3 (r-3) = 0
(r – 3)(9r – 3) = 0
r = 3 or 9r = 3
r = 3 or r = \(\frac{3}{9}=\frac{1}{3}\)
r = 3 or r = \(\frac{1}{3}\)

The numbers are \(\frac{a}{3}\),a,ar
\(\frac{9}{3}\), 9, 9(3)
3,9,27.

Question 31.
Find the quotient and remainder when x⁴ + 10x³ + 39x² + 76x + 65 is divided by x +4.
Answer:

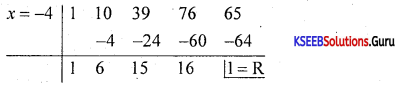
Quotient = x³ + 6x² + 15x + 16
Remainder = 1

Question 32.
Solve graphically : x + 2y < 8, 2x + y < 8
Answer:

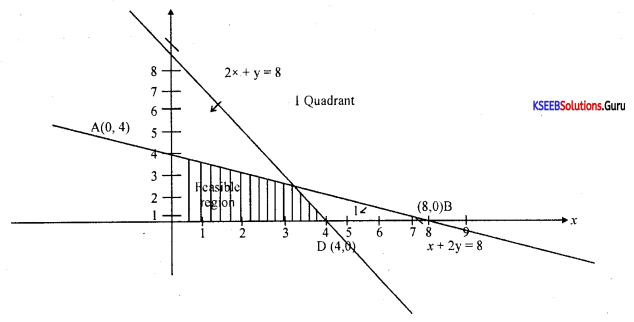
Question 33.
Find the compound interest on ₹ 7000 at 5% p.a for 4 years?
Answer:
A = P(l + i)ⁿ ⇒ A = 7000(1 + 0.05)⁴ = 8508.54
CI – A – P = 8508.54 – 7000 ⇒ Cl = ₹ 1508.54

Question 34.
Ramya purchased 3 varieties of cooking oil 4 kg of oil at ₹ 50/kg. 5 kg of oil at ₹ 60/ kg and 9 kg of oil at ₹ 70/kg. What is the average price of oil/kg?
Answer:
X̄w = \(\frac{x_{1} w_{1}+x_{2} w_{2}+x_{3} w_{3}}{w_{1}+w_{2}+w_{3}}=\frac{50 \times 4+60 \times 5+70 \times 9}{4+5+9}=\frac{1130}{18}\) = ₹ 63.2 /kg

Question 35.
The price of a pair of trousers was decreased by 22% of ₹ 390. What was the original price of the trousers.
Answer:
Let the original price be x. .
Then (x – \(\frac{22 x}{100}\)) = 390 ⇒ x(1 – \(\frac{22}{100}\)) = 390 ⇒ x\(\frac{78}{100}\) = 390
x = \(\frac{390 \times 100}{78}\) = ₹ 500

Question 36.
Find the value of \(\frac{\sin \frac{\pi}{2} \cos ^{2} \frac{\pi}{6} \sec ^{2} \frac{\pi}{4}}{\tan \frac{\pi}{3}+\cot \frac{\pi}{3}}\)
Answer:
\(\frac{\sin \frac{\pi}{2} \cos ^{2} \frac{\pi}{6} \sec ^{2} \frac{\pi}{4}}{\tan \frac{\pi}{3}+\cot \frac{\pi}{3}}=\frac{1 \times\left(\frac{\sqrt{3}}{2}\right)^{2} \cdot(\sqrt{2})^{2}}{\sqrt{3}+\frac{1}{\sqrt{3}}}=\frac{\frac{\sqrt{3}}{4} \times 2}{\frac{(\sqrt{3})^{2}+1}{\sqrt{3}}}=\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{4}=\frac{3}{8}\)

Question 37.
Find the third vertex of a triangle if two of its vertices are at (-2, 4) and (7, -3) and the centroid at (3, -2).
Answer:
Centroid G(x, y) = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
(3, 2) = \(\left(\frac{-2+7+x_{3}}{3}, \frac{4-3+y_{3}}{3}\right)\) ⇒ x₃ = 4, y₃ = -7
∴ Third vertex (x₃, y₃) = (4, -7)

Question 38.
Find the distance between the two lines 2x – 3y + 4 = 0 and 4x – 6y – 5 = 0.
Answer:
Distance between parallel lines = \(\left|\frac{c_{1}-c_{2}}{\sqrt{a^{2}+b^{2}}}\right|=\left|\frac{8-(-5)}{\sqrt{4^{2}+(-6)^{2}}}\right|=\frac{13}{\sqrt{52}}=\frac{\sqrt{13}}{2}\) units

Part – D

IV. Answer any SIX questions. (6 × 5 = 30)

Question 39.
In a group of 50 people, 35 speak Kannada and 25 speak both English and Kannada and all the people speak at least one of the two languages. How many speak English? How many speak only English and not Kannada? How many speak only Kannada?
Answer:
n(K ∪ E) = n[K) + n(E) – n(K ∩ E)
50 = 35 + n(E) – 25 ⇒ K(E) = 40
(i) n(E-K) = n(E)-n(E∩K) = 40-25 = 15
(ii) n(K-E) = n(K) – n[K ∩ E) = 35 -25 = 10

Question 40.
Evaluate \(\frac{213.78 \times 7.434}{6.321}\) using logarithmic tables.
Answer:
Let x = \(\frac{213.781 \times 7.434}{6.321}\)
logx = \(\left[\frac{213.781 \times 7.434}{6.321}\right]\)
= log213.781 + logl.434 – log6.321
= 2.3298 + 0.87 12 –0.8008.
= 2.4002
x = Antilog 2.4002
x = 25 1.3.

Question 41.
Find the sum of all numbers between 60 and 400 which are divisible by 13.
Answer:
S_n = 65 + 78 + 91 +…………..+390
a = 5 d = 13 n =? T_n = 390
T_n = a + (n – 1)d
390 = 65 + (n – 1)13
390 = 65 + 13n – 13
13n = 338
∴ n=26
S_n = \(\frac{n}{2}\)[a + l] = (65+390) = 13 (455)= 5,915
∴ S = 5,915

Question 42.
A mother is 32 years older than her son. After 4 years the mother’s age will be 8 years more than twice that of her son. Find their present ages.
Answer:
Let the present age of the son = x yrs.
and the present age of the mother = x + 32 years
After 4 years age of the mother = x + 36
Given that x + 36 = 8 + 2 (x + 4) = 8 + 2x + 8
36 – 16 = 2x – x
x = 20 years
∴ son’s present age is x = 20 yrs
mother’s present age is 20 + 32 = 52 years.

Question 43.
Find the difference between simple interest and compound interest on ₹ 18,000 invested for 4 years at 8% p.a. where compound interest is compounded annually.
Answer:
Simple Interest
P = 18,000 T = 4 R = 4
SI = \(\frac{\mathrm{PTR}}{100}\)
= \(\frac{18,000 \times 4 \times 8}{100}\)
= ₹5,760

Compound Interest
P = 18,000 n = 4 I = 008
A = P(1 + i)n
= 18,000 (1 + 0.08)4
= 24,488.8
CI = A – P
= 24,488.8 – 18,000
CI = 6488.8

Difference between CI and Si is
CI – SI = 6488.8, – 5760
= 728.8.

Question 44.
If you want to have ₹ 80,000 after 5 years, how much should you deposit every year if the bank offers 12% p.a. interest compounded quarterly.
Answer:
F = 80,000, n = 5yrs, r 12% 0.12, i = \(\left(1+\frac{0.12}{4}\right)^{4}\) – 1 = 0.125
F = \(\frac{a\left[(1+i)^{n}-1\right]}{i}\)
a = \(\frac{\mathrm{F} \times i}{(1+i)^{n}-1}=\frac{80,000 \times 10.125}{(1.125)^{5}-1}=\frac{80,000}{6.416}\) = ₹12,468.8

Question 45.
A businessman sells an article for ₹ 720 and earns a profit of 20% Find the (a) cost price (b) profit percentage at the selling price.
Answer:
S.P = 720 = \(\frac{120}{100}\)x ⇒ x = \(\frac{720 \times 100}{120}\) = 600
∴ Profit = 720 – 600 = 120 ⇒ profit% = \(\frac{\text { profit in Rs. }}{\text { S.P. }}\) × 100 = \(\frac{120}{720}\) × 100 = 16.66%

Question 46.
If cot \(\frac{\theta}{2}=\frac{5}{2}\) q is acute. Show that \(\frac{3 \cos \theta+2 \sin \theta}{3 \cos \theta-4 \sin \theta}=\frac{19}{7}\)
Answer:
cotθ = \(\frac{5}{2}\) ∴ Hyp = \(\sqrt{29}\)
cosθ = \(\frac{5}{\sqrt{29}}\), sinθ = \(\frac{2}{\sqrt{29}}\)

Substituting and simplifying we get
LHS = \(\frac{3 \cos \theta+2 \sin \theta}{3 \cos \theta-4 \sin \theta}=\frac{3 \cdot \frac{5}{\sqrt{29}}+2 \cdot \frac{2}{\sqrt{29}}}{3 \cdot \frac{5}{\sqrt{29}}-4 \cdot \frac{2}{\sqrt{29}}}=\frac{15+4}{15-8}=\frac{19}{7}\)

Question 47.
Find the ratio in which the line joining the points (3, 5) and (-7, 9) ¡s divided by the point (\(\frac{1}{2}\),6).
Answer:

Question 48.
Find the equation of a line that passes through (-4, 1), and a portion of it between the axes is divided by the point in the ratio 1:2.
Answer:
A straight line passes through the point (-4, 7) and the portion of the line intercepted between the axes is divided at this point in the ratio 3: 2. Find the equation of the line.

Let the required equation of the line be
\(\frac{\mathrm{x}}{\mathrm{a}}+\frac{\mathrm{y}}{\mathrm{b}}\) = 1 …………(1)
Then it meets the axes at the points A (a, 0) and B (0, b). The coordinates of the point which divides the line AB in the ratio 3: 2 are
\(\left(\frac{2 \cdot a+3 \cdot 0}{2+3}, \frac{2 \cdot 0+3 \cdot b}{2+3}\right)=\left(\frac{2 a}{5}, \frac{3 b}{5}\right)\) …….(2)
This is the same as (-4, 7) ……………(3)
Comparing (2) and (3), \(\frac{2 a}{5}\) =-4, \(\frac{3b}{5}\) = 7 or a = -10, b = \(\frac{35}{3}\)
Substituting these values of a, b in (1) we get
\(\frac{x}{-10}+\frac{y}{\frac{35}{3}}\) = 1

Part – E

V. Answer any ONE question. (1 × 10 = 10)

Question 49.
(a) Find the sum to n terms of the series 5 + 55 + 555 +………..n terms.
Answer:
Let S = 5 + 55 + 555 + ………. to n terms
\(\frac{S}{2}\) = 1 + 11 + 111 +……….to n terms
\(\frac{9S}{2}\) = 9 + 99 + 999 +…………….to n terms
(10 – 1) + (100 – 1) + (1000 – 1) +………… to n terms
= (10 + 100 + 1000 + to n terms) – (1 + 1 + to n terms)
= \(\frac{10\left(10^{n}-1\right)}{9}\) – 1 × n
S = \(\frac{5}{9}\left[\frac{10\left(10^{n}-1\right)}{9}-n\right]\)

(b) A manufacture produced and sells balloons at ₹ 8 per unit. His fixed cost is X 6500 and the variable cost per balloon is ₹ 3.50. Calculate
(i) Revenue function (ii) Cost function (iii) Profit function (iv) Break even point
Answer:
Manufacture produceçi and sells balloons at ₹ 8 per unit. His fixed cost is ₹ 6500 and the variable cost per Balloon is ₹ 3.50 calculate,

1. Revenue Function
2. Cost Function
3. Profit Function
4. Break-Even point.

i.e. (i) R(x) = 8x

(ii) C(x) = 3.5x + 6500

(iii) P(x) = 4.5x – 6500
i.e.,P(x) = 6500 = 0

(iv) At BEP P(A) = 0
4.5x – 6500 = 0
4.5x = 6500
x = 144.4 units

(c) The weight of 6 men are 90 kg, 70.5 kg, 56 kg, 45.5 kg, 85 kg and 78 kg. Find the average weight.
Answer:
Average weight of 6 men = \(\frac{90+70.5+56+45.5+85+78}{6}=\frac{425}{6}\) = 70.83 kg

Question 50.
(a) Find the equation of the straight line which passes through the point of intersection of 2x – 3y = 4 and 2x + 2y = 1 and perpendicular to the line x + 4y = 8.
Answer:

(b) If A = (1, 3, 5) B = {5} C = {7} verify A × (B – C) = (A × B) – (A × C)
Answer:
B – C = {5}
A × (B -C) = {1,3,5} × {5} ={(1,5), (3,5), (5,5)}…………………. (1)
A × B= {(1,5), (3,5), (5,5)}
A × C = {(1,7), (3,7), (5,7)}
(A × B) – (A × C) = {(1,5), (3,5), (5,5)} ………..(2)
From (1) and (2), A – (B – C) = (A × B) – (A × C)

(c) If the HCF of two numbers is 42 and their product is 52920, find their LCM.
Answer:
H.C.F × L.C.M = A × B
42 × LCM = 52920 ⇒ LCM = \(\frac{52920}{42}\) = 1260
∴ LCM = 1260