Karnataka 1st PUC Economics Question Bank Chapter 6 Measures of Dispersion
1st PUC Economics Measures of Dispersion TextBook Questions and Answers
I. Choose the correct answers
Question 1.
Inter quartile range is based upon middle _______of the values in a distribution.
(a) 30%
(b) 20%
(c) 50%
(d) 25%
Answer:
(c) 50%
Question 2.
For QD, we need to calculate values of Q3 and
(a) Q2
(b) Q4
(c) Q1
(d) Q0
Answer:
(c) Q1.
Question 3.
Coefficient of range = _______
(a) \(\frac{\mathbf{L}-\mathbf{S}}{\mathbf{L}+\mathbf{S}}\)
(b) \(\frac{\mathbf{R}-\mathbf{L}}{\mathbf{R}+\mathbf{L}}\)
(c) \(\frac{\mathbf{L}+\mathbf{S}}{\mathbf{L}-\mathbf{S}}\)
(d) None of the these
Answer:
(a) \(\frac{\mathbf{L}-\mathbf{S}}{\mathbf{L}+\mathbf{S}}\)
Question 4.
What is the graphical measure available to measure dispersion?
(a) Lorenz curve
(b) Marshal curve
(c) Production curve
(d) None of the these
Answer:
(a) Lorenz curve
II. Answer the following questions in a word or sentence
Question 1.
What is dispersion? (S – 2018) (N – 2018)
Answer:
Dispersion refers to the extent to which values in a distribution differ from the average of the distribution
Question 2.
How do range and quartile deviation measure the dispersion?
Answer:
Range and quartile deviation measure the dispersion by calculating the spread within which the values lie
Question 3.
How do means deviation and standard deviations measure dispersion?
Answer:
The mean deviation and standard deviations measure dispersion by calculating the extent to which the values differ from the average.
Question 4.
Give the meaning of standard deviation.
Answer:
Standard deviation is the positive square root of the mean of squared deviations from the main
Question 5.
Write the formula to calculate the coefficient of variation.
Answer:
The coefficient of variation can be calculated with the help of the following formula:
Coefficient of variation = \(\frac{\text { Standard deviation }}{\text { Arithmetic mean }}\) × 100
III. Answer the following questions in about four sentences
Question 1.
Which quartiles are used to calculate the interquartile range? Give the formula of it.
Answer:
Tire upper and lower quartiles are used to calculate interquartile range. It is calculated by using the formula.
Interquartile range = Q3 – Q1
Question 2.
What is the mean deviation? Which average is used to find it? (N – 2018)
Answer:
Mean deviation is the arithmetic mean of the differences of the values from their average. The average used is either arithmetic mean or median.
IV. Answer the following questions in about twelve sentences
Question 1.
The yield of wheat per acre for 10 districts of a state are as follows:

Calculate quartile deviation (QD)
Answer:
QD for Wheat
First, we need to arrange the observations in tire ascending order
x: 9 10 10 12 15 16 18 19 21 25
Calculation of lower quartile (Q1)
Q1 = Size of \(\left(\frac{N}{4}\right)^{\text {th }}\) item = Size of \(\left(\frac{10+1}{4}\right)^{t h}\) item
= size of \(\left(\frac{11}{4}\right)^{\text {th }}\) item
i.e. 2.75th item
The size of 2.75th item is size of 2nd item + 0.75 item
Size of 2nd item =10
Size of 0.75 item = Size of 3rd item – 2nd item)
= 10 – 10 = 0
∴ Q1 = size of 2nd item + 075 item is
Q1 = 10 + 0.75(10 – 10)
= 10 + 0.75(0)= 10 + 0
Q1 = 10
Calculation of Upper Quartile (Q3)
Q3 = Size of 3\(\left(\frac{N+1}{4}\right)^{\text {th }}\) item
= Size of 3\(\frac{3(10+1)^{\text {th }}}{4}\) item = Size of \(\left(\frac{3(11)}{4}\right)^{th}\) item
= Size of \(\left(\frac{33}{4}\right)^{t h}\) item = Size of 8.25th item
i.e.. size of 8th item + 0.25 item (size of 9th – 8th item)
Q3 = 19 + 0.25(21 – 19)
Q3 = 19 + 0.25(2)
Q3 = 19 + 0.5
Q3 = 19.5
Now QD= \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}=\frac{19.5-10}{2}=\frac{9.5}{2}\) =4.75
QD = 4.75 tonnes
Question 2.
The yield of rice per acre for 10 districts of a state is as under (Board Paper)

Calculate quartile deviation (QD)
Answer:
QD for rice:
Arrange the given observations in ascending order.
x : 12 12 12 15 18 18 22 23 29 34
Calculation of lower quartile (Q1 )
Q1 = Size of \(\left(\frac{\mathrm{N}+1}{4}\right)^{\mathrm{th}}\) item
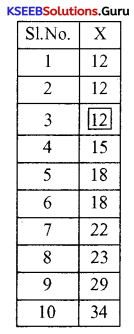
= Size of \(\left(\frac{10+1}{4}\right)^{t h}\) item = Size of \(\left(\frac{11}{4}\right)^{t h}\) item
= Size of 2.75th item
The size of 275th item = size of item + 0.75 item
(0.75 item size of 3rd item – size of 2’nd item)
∴ Q1= 12 + 0.75(12 – 12)
Q1 = 12 +0.75 (0)
Q1 = 12
Calculation of upper quartile (Q3)
Q3 = Size of \(\left(\frac{N+1}{4}\right)^{t h}\) item = Size of \(\frac{3(10+1)^{t h}}{4}\) item
= Size of \(\frac{3(11)^{\text {th }}}{4}\) item = Size of \(\left(\frac{3(11)}{4}\right)^{\text {th }}\) item
= Size 0f 8.25th item
The size of 825th item = size of 8th item + 0.25 items
(0.025 item = size 0f 9th item – size of 8th item)
∴ Q3 = size of 8.25th item i.e.,
Q3 = 23 + 0.25 (29 – 23) = 23 + 0.25 (6)
= 23 + 1.5
Q3 = 24.51
Quartile deviation = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}=\frac{24.5-12}{2}\)
= \(\frac{12.5}{2}\) = 6.25
QD = 6.25 tonnes
Question 3.
The yield of wheat per acre for 10 districts of a state is as under:

Calculate mean Deviation from Mean value.
Answer:
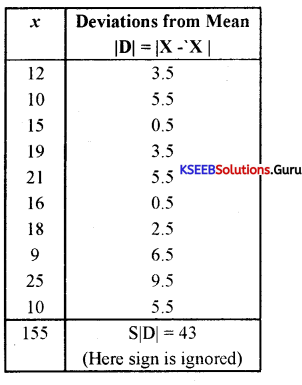
Mean(X̄) = \(\frac{\Sigma x}{N}=\frac{155}{10}\) = 15.5 N 10
∴ X̄ = 15.5
MD from Mean = \(\frac{\Sigma|\mathrm{D}|}{\mathrm{N}}=\frac{43}{10}\) = 4.3 tonnes
∴ MDX̄ = 4.3 tonnes
Question 4.
The yield of rice per acre for 10 districts of a state is as under:

Calculate mean deviation from the mean.
Answer:
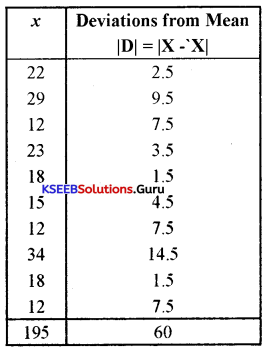
X̄ = \(\frac{\Sigma x}{\mathrm{~N}}=\frac{195}{10}\) = 19.5
∴ X̄ = 19.5
MD from mean = \(\frac{\Sigma|D|}{N}=\frac{60}{10}\) = 6
∴ MDX̄ = 6 tonnes
Question 5.
The yield of wheat per acre for 10 districts of a state is as under:

Calculate the mean deviation from the median. (S – 2018)
Answer:
First, we need to write the ie1d of what in arc ascending order
x: 9 10 10 12 15 16 18 19 21 25
Median = Size of \(\left(\frac{N+1}{2}\right)^{\text {th }}\) item
= Size of \(\left(\frac{10+1}{2}\right)^{\text {th }}\) item
= Size of \(\left(\frac{11}{2}\right)^{\text {th }}\) item
= Size of 5.5th item
To get the median, we need to add the 5th and 6th items and the same divided by 2.
Median = \(\frac{5^{\text {th }} \text { item }+6^{\text {th }} \text { item }}{2}=\frac{15+16}{2}=\frac{31}{2}\) = 15.5
Median = 15.5
Calculation of mean deviation from the median
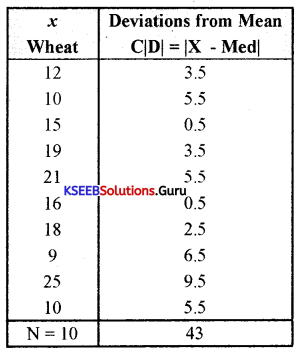
Mean deviation from the median (MDXm)
MDM = \(\frac{\sum|\mathrm{D}|}{\mathrm{N}}=\frac{43}{10}\) = 4.3
∴ MDM = 4.3 tonnes
Question 6.
The yield of rice per acre for 10 districts of a state is as under:

Calculate mean deviation from the median.
Answer:
Values in ascending order
x : 12 12 12 15 18 18 22 23 29 34
Median = Size of \(\left(\frac{\mathrm{N}+1}{2}\right)^{\mathrm{th}}\) item
Median = Size of \(\left(\frac{10+1}{2}\right)^{\text {th }}\) item
= Size of \(\left(\frac{11}{2}\right)^{\text {th }}\) item
= 5.5th item
To get median, we need to add 5th and 6th items and divide it by 2.
Median = \(\frac{5^{\text {th }} \text { item }+6^{\text {th }} \text { item }}{2}=\frac{18+18}{2}=\frac{36}{2}\) = 18
∴ Median = 18
Calculation of mean deviation from median:
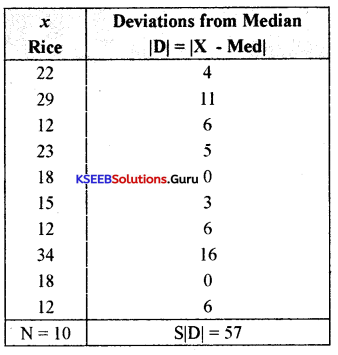
Mean deviation from median (MDM )
MDM = \(\frac{\Sigma|\mathrm{D}|}{\mathrm{N}}=\frac{57}{10}\) = 5.7
MDM = 5.7 tonnes
Question 7.
Calculate the Mean Deviation using the mean for the following distribution.
| Class Interval | Frequency |
| 20-40 | 3 |
| 40-80 | 6 |
| 80-100 | 20 |
| 100-120 | 12 |
| 120-140 | 9 |
| 50 |
Answer:
Calculation of mean deviation from mean
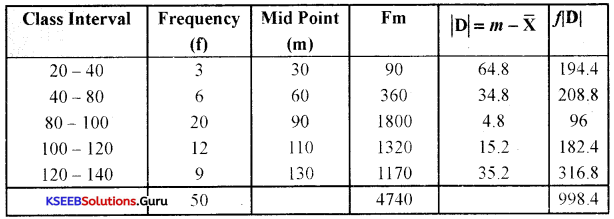
X̄ = \(\frac{\Sigma f m}{n}=\frac{4740}{50}\) = 94.8
X̄ = 94.8
Mean deviation from mean (MDX̄)
MDX̄ = \(\frac{\Sigma \mathrm{f}|\mathrm{D}|}{\mathrm{N}}=\frac{998.4}{50}\) = 19.97
∴ MDX̄ = 19.97
Question 8.
Calculate the QD and its coefficient for the following data.
78, 80, 80, 82, 82, 84, 84, 86, 86, 88, 88, 90.
Answer:
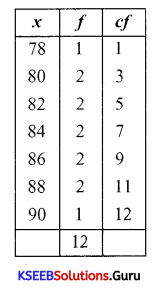
We know that QD = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
So, to calculate QD we need to calculate Q3 and Q1.
Q3 = Size of \(\frac{3(\mathrm{~N}+1)^{\mathrm{th}}}{4}\) item = Size of \(\frac{3(12+1)}{4}\)th item
Q3 = Size of \(\left(\frac{3(13)}{4}\right)^{\text {th }}\) item = Size of \(\left(\frac{39}{4}\right)^{\mathrm{th}}\) item
Q = Size of 9.75th item
i.e., size of 9th + 0.75 (10th – 9th items)
Q = 86 + 0.75(88 – 6) = 86 + 0.75(2) = 86 + 1.5
Q3 = 87.5
Q1 = Size of \(\left(\frac{\mathrm{N}+1}{4}\right)^{\mathrm{th}}\) item = Size of \(\left(\frac{12+1}{4}\right)^{\text {th }}\) item
= Size of \(\left(\frac{13}{4}\right)^{\mathrm{th}}\) item = Size of 3.25th item
i.e., 3rd + 0.25 (4th – 3 item)
∴ Q1 = 80 + 0.25 (82 – 80) = 80 + 0.25 (2)
Q1 = 80 + 0.5
Q1 =80.5
Now to get quartile deviation (QD)
QD = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}=\frac{87.5-80.5}{2}=\frac{7}{2}\)
Q.D = 3.5
Coefficient of QD = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{\mathrm{i}}}=\frac{87.5-80.5}{87.5+80.5}=\frac{7}{168}\) = 0.0416
Question 9.
Calculate the mean deviation from mean and its coefficient for the following data
1100,150, 200,360, 490, 500, 600.
Answer:
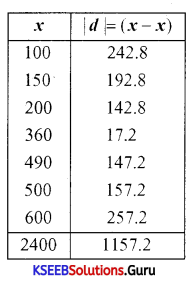
x̄ = \(\frac{2400}{7}\)
x̄ = 342.8
M.Dx̄ = \(\frac{\Sigma|d|}{\mathrm{N}}=\frac{1157.2}{7}\)
M.Dx̄ = 165.31
Coefficient of MD = \(\frac{\mathrm{MD}_{\bar{x}}}{\overline{\mathrm{X}}}=\frac{165.31}{342.8}\) = 0.482
Question 10.
Calculate MD from the median and its relative measure for the following data
37,45,52,46,56, 40,47,55, 43.
Answer:
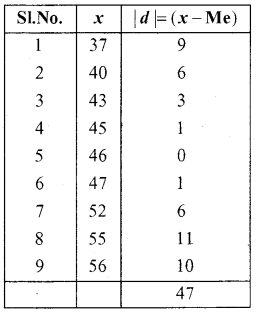
Median = Size of \(\left(\frac{\mathrm{N}+1}{2}\right)^{\mathrm{th}}\) item
= Size of \(\left(\frac{9+1}{2}\right)^{\text {th }}\) item
= Size of \(\left(\frac{10}{2}\right)^{t h}\) item = 5th item
Median = 46
M.Dme = \(\frac{\Sigma|d|}{N}=\frac{47}{9}\) = 5.22.
M.Dme = 5.22
Relative measure i.e., co-efficient of MD from median
Coefficient MDme = \(\frac{\mathrm{MD}_{\mathrm{me}}}{\mathrm{M}}=\frac{5.22}{46}\) = 0.113
Relative measure i.e.. co-efficient of MD from median is 0.113.
Question 11.
Find the mean deviation from the mean for the following distribution.

Answer:
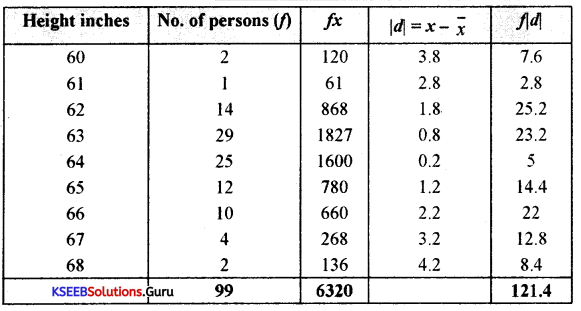
x̄ = \(\frac{\Sigma f x}{N}=\frac{6320}{99}\) = 63.8
x̄ = 63.8
M.Dx̄ = \(\frac{\Sigma f|d|}{\mathrm{N}}=\frac{121.4}{99}\)
M.Dx̄ = 1.22
Question 12.
Calculate the coefficient of MD from the median for the following frequency distribution.

Answer:
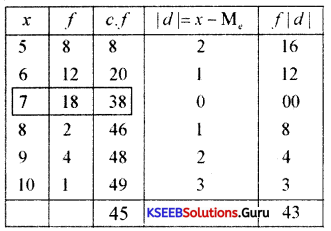
Median = Size of \(\left(\frac{\mathrm{N}+1}{2}\right)^{\mathrm{th}}\) item = Size of \(\left(\frac{45+1}{2}\right)^{t h}\) item
Median = Size of \(\left(\frac{46}{2}\right)^{\text {th }}\) item = Size of 23rd item i.e:, 7
Median = 7
MD = \(\frac{\sum f|d|}{N}=\frac{43}{45}\) = 0.95
Coefficient of MDme = \(\frac{\mathrm{MD}_{\mathrm{me}}}{\mathrm{M}_{\mathrm{me}}}=\frac{0.95}{7}\) = 0.13
MDMe = 0.95
Question 13.
Find M.D. from the mean for the following distribution regarding the difference in ages (years) between husband and wife of a particular community.

Answer:
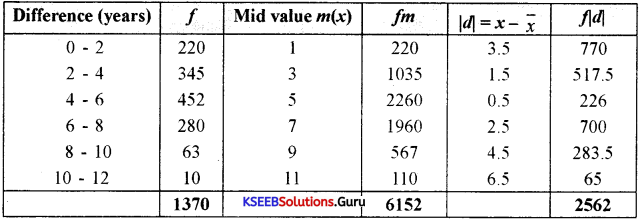
x̄ = \(\frac{\Sigma f m}{n}=\frac{6152}{1370}\) = 4.49 (4.5)
MDx̄ = \(\frac{\Sigma f|d|}{\mathrm{N}}=\frac{2562}{1370}\) = 1.87
MDx̄ = 1.87
Question 14.
Find the standard deviation for the following data:
8, 9,15, 23, 5,11,19, 8,10, 12.
Answer:
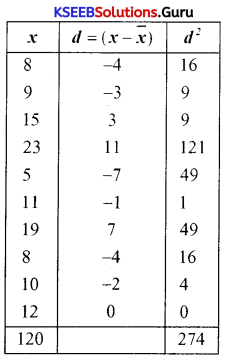
x̄ = \(\frac{\sum x}{N}=\frac{120}{10}\)
x̄ = 12
σ = \(\sqrt{\frac{\Sigma d^{2}}{n}}=\sqrt{\frac{274}{10}}=\sqrt{27.4}\)
σ = 5.23
Question 15.
Find the standard deviation of the following data by the deviation method.
25, 50, 45, 30, 70,42, 36,48, 34, 60.
Answer:
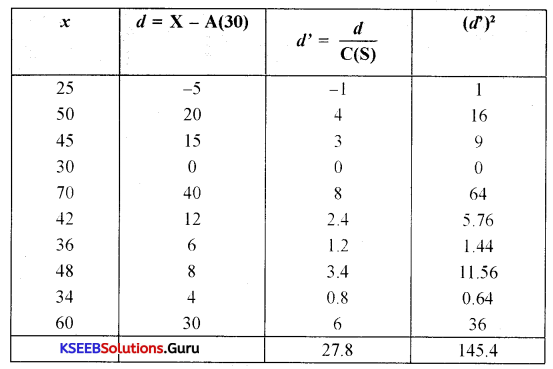
σ = \(\sqrt{\frac{\sum d^{12}}{n}-\left(\frac{\Sigma d^{1}}{n}\right)^{2}}\) × C = \(\sqrt{\frac{145.4}{10}-\left(\frac{27.8}{10}\right)^{2}}\) × 5
σ = \(\sqrt{14.54-(2.78)^{2} \times 5}=\sqrt{14.54-7.72 \times 5}=\sqrt{6.82}\) × 5 = 2.61 × 5
σ = 13.05
V. Answer the following in about twenty sentences (each question carries 6 marks)
Question 1.
The yield of wheat per acre for 10 districts of a state are as under:

Calculate standard deviation and coefficient of variation (N – 2018)
Answer:
Standard Deviation (actual mean method)
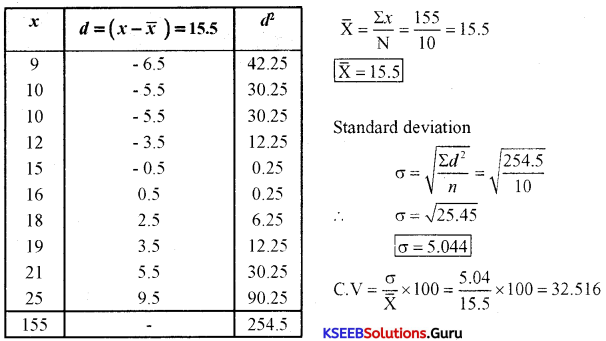

Question 2.
The yield of rice per acre for 10 districts of a state is as under:

Calculate standard deviation and coefficient of variation.
Answer:
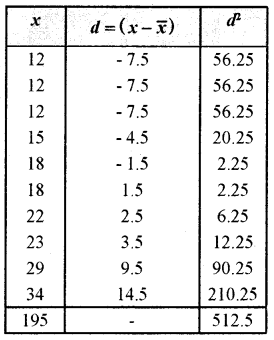

Question 3.
A batsman is to be selected for a cricket team. The choice is between X and Y on the basis of their scores in five previous tests which are:

Which batsman should be selected if we want,
(i) a higher run-getter, or
(ii) a more reliable batsman in the team?
Answer:
(i) To determine a higher run-getter, we need to find out the average of both the batsman
X̄ = \(\frac{\Sigma x}{N}\)
X̄ = \(\frac{350}{5}\) = 70 Runs
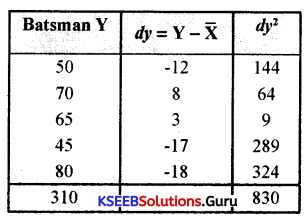
X̄ = \(\frac{\Sigma X_{y}}{N}=\frac{310}{5}\) = 62 Runs
Batsman X: 70 Runs
Batsman Y: 62 Runs
Batsman ‘X’ should be selected on the basis of runs scored as his average runs are more than that of Batsman Y.
(ii) To determine a reliable batsman, we need to calculate coefficient of variation (CV)

Question 4.
To check the quality of the two brands of light bulbs, their life in burning hours was estimated for 100 bulbs of each brand as shown below.
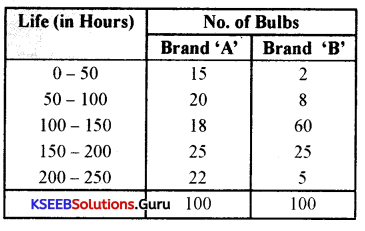
(i)Which brand gives longer life?
(ii) Which brand is more dependable?
Answer:
To know which brand gives a longer life we need to calculate the average life of both the brands. To know the most dependable brand we need to find out the coefficient of variation (CV).
Brand ‘A’
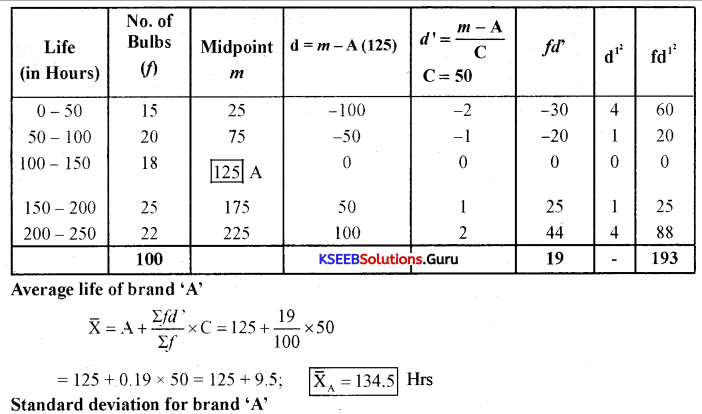

Brand ‘B’


(i)Brand B has a longer life average
(ii) Brand B is more dependable.
Question 5.
Calculate the standard deviation for the following distribution.
| Class Interval | Frequency |
| 20-40 | 3 |
| 40-80 | 6 |
| 80-100 | 20 |
| 100-120 | 12 |
| 120-140 | 9 |
| 50 |
Answer:
Calculation of SD (σ)

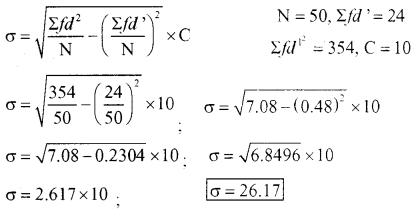
Question 6.
Calculate the coefficient of QD for the following distribution.

Answer:
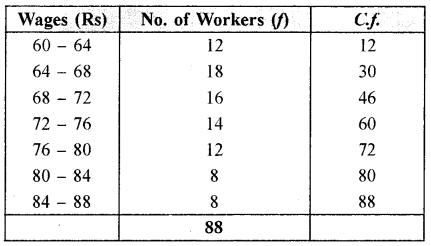
QD = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
Q1 = \(\left(\frac{n}{4}\right)^{\text {th }}\) item = \(\left(\frac{88}{4}\right)^{\text {th }}\) = 22nd item
Q1 falls in 64-68
To find the exact Q1 the following formula is used:
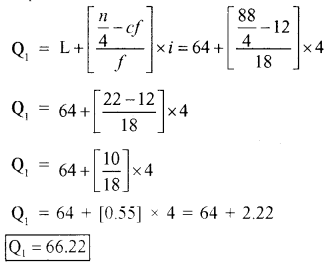
Now to calculate Q3
Q3 = Size of \(\left(\frac{3(n)}{4}\right)^{t h}\) item = Size of \(\frac{3(88)^{\text {th }}}{4}\) item
= Size of \(\left(\frac{264}{4}\right)^{\text {th }}\) item = Size of 66 item
So the Q3 falls in 76 – 80
To calculate the exact Q3 the folloing formula is used

QD = 5.89
Coefficient of quartile deviation
= \(\frac{Q_{3}-Q_{1}}{Q_{3}+Q_{1}}=\frac{78-66.22}{78+66.22}=\frac{11.78}{144.22}\)
Coefficient of QD = 0.0816
Question 7.
Calculate QD and its relative measures for the following distribution.

Answer:
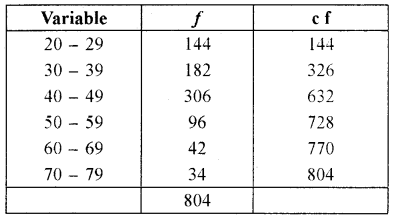
QD = \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{2}\)
Q1 = Size of \(\left(\frac{n}{4}\right)^{\text {th }}\) item = Size of \(\left(\frac{804}{4}\right)^{th}\) = Size of 201st item
So, Q1 lies in 30 – 39
To find exact Q1 the following formula is used.
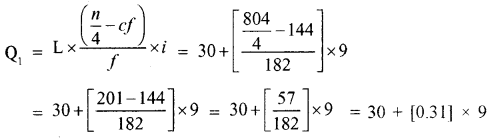
Q1 = 30 + 2.81;
Q1 = 32.81
Now to calculate Q3
Q3 = Size of \(\left(\frac{3(n)}{4}\right)^{t h}\)item = Size of \(\left(\frac{3(804)}{4}\right)^{t h}\) item
= Size of \(\left(\frac{2412}{4}\right)^{\mathrm{th}}\) item = Size of 603rd item
So, Q3 lies in 40 – 49
To find the exact Q3 following formula is used.
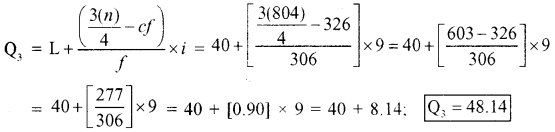
A relative measure of QD
Coefficient of QD
= \(\frac{\mathrm{Q}_{3}-\mathrm{Q}_{1}}{\mathrm{Q}_{3}+\mathrm{Q}_{1}}=\frac{48.14-32.81}{48.14+32.81}=\frac{15.33}{80.95}\)
Coefficient of Q.D = 0.189
Question 8.
Calculate the standard deviation and variance for the following distribution by deviation method

Answer:
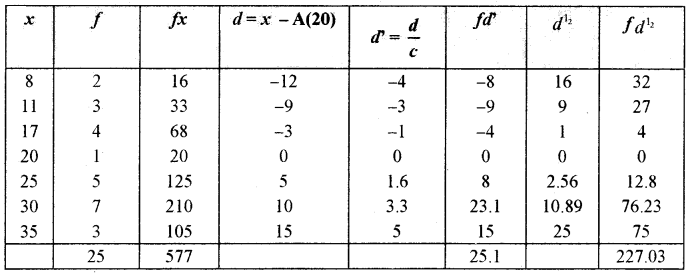

Question 9.
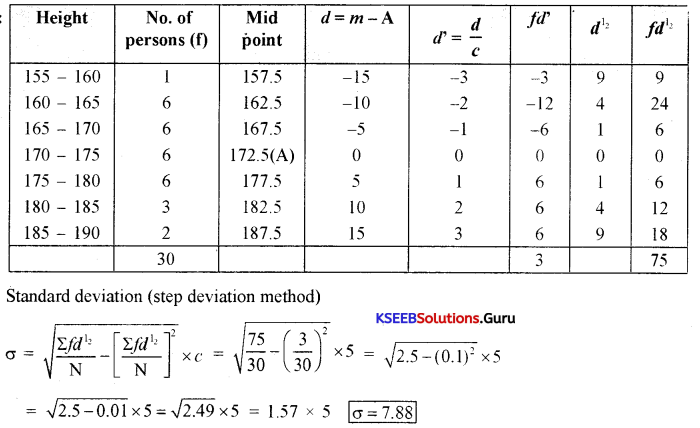
Calculate the SD for the following frequency distribution of heights of 30 persons by the direct method. (S – 2018)

Answer:
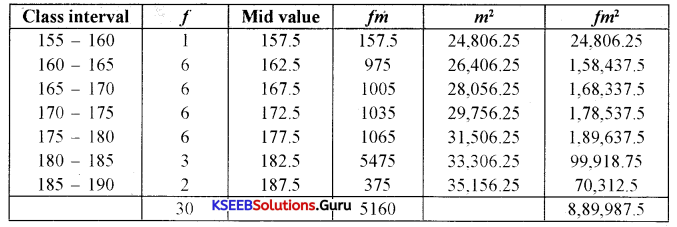
x̄ = \(\frac{\Sigma f m}{n}=\frac{5160}{30}\) = 172
x̄ = 172
Standard deviation (direct method)
σ = \(\sqrt{\frac{\Sigma f m^{2}}{N}-(\bar{x})^{2}}=\sqrt{\frac{8,89,987.5}{30}-(172)^{2}}=\sqrt{29,666.25-29,584}=\sqrt{82.25}\)
σ = 9.06
Question 10.
Calculate the SD for the following frequency distribution of heights of 30 persons by the step deviation method.

Answer: