You can Download Chapter 4 Principle of Mathematical Induction Questions and Answers, Notes, 1st PUC Maths Question Bank with Answers, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 1st PUC Maths Question Bank Chapter 4 Principle of Mathematical Induction
Question 1.
Using the principle of mathematical induction, prove that
\(\text { (1) } 1+2+3+\cdots+n=\frac{n(n+1)}{2}\), for all n∈N
Answer:

which is P(k +1)
Thus, P(k)⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
![]()
Question 2.
1 + 3 + 5 + 7 + …….. + (2n – 1) = n2, for all n∈N
Answer:
Let P(n):1 + 3 + 5 + 7+……….. +(2n-1) = n2
For n = 1, LHS = 1, RHS = 12 = 1
∴ LHS = RHS
∴ F(1) is true.
Let upwards assume P(k) is true for some k∈N
i.e., 1 + 3 + 5 + …. + (2K- 1) = kz
Adding (k + 1)th term = 2K + 1, on both sides, we get,
1 + 3 + 5 +……. +(2k -1)(2k + l) = k2 + 2k + 1
= (k +1)2
which is P(k +1)
Thus, P(k)⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 3.
\(1^{2}+2^{2}+3^{2}+\ldots \ldots+n^{2}=\frac{n(n+1)(2 n+1)}{6}\)
Answer:

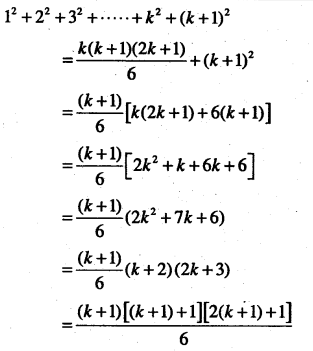
which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
![]()
Question 4.
\(1^{3}+2^{3}+3^{3}+\ldots \ldots+n^{3}=\left[\frac{n(n+1)}{2}\right]^{2} \) for all n∈N
Answer:

which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 5.
\(1 \cdot 2+2 \cdot 3+\dots+n(n+1)=\frac{n(n+1)(n+2)}{3}\) for all n∈N
Answer:

which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 6.
\( \begin{aligned} &1 \cdot 2 \cdot 3+2 \cdot 3 \cdot 4+\dots+n(n+1)(n+2)&=\frac{n(n+1)(n+2)(n+3)}{4},
\text { for all } n \in N \end{aligned}\)
Answer:

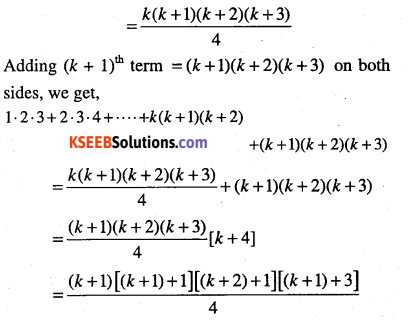
which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 7.
\( \cfrac{1}{1 \cdot 2}+\cfrac{1}{2 \cdot 3}+\cfrac{1}{3 \cdot 4}+\dots+\cfrac{1}{n(n+1)}=\cfrac{n}{n+1}\) for all n∈N
Answer:

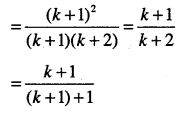
which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 8.
\(\begin{aligned} &\cfrac{1}{1 \cdot 2 \cdot 3}+\cfrac{1}{2 \cdot 3 \cdot 4}+\cfrac{1}{3 \cdot 4 \cdot 5}+\dots+\cfrac{1}{n(n+1)(n+2)}&=\cfrac{n(n+3)}{4(n+1)(n+2)}, \text { for all } n \in N \end{aligned}\)
Answer:

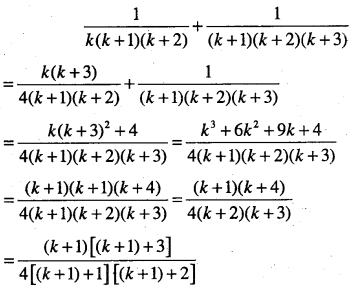
which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
![]()
Question 9.
\( \begin{aligned}&\frac{1}{2 \cdot 5}+\frac{1}{5 \cdot 8}+\frac{1}{8 \cdot 11}+\cdots \cdot+\\ &\frac{1}{(3 n-1)(3 n+2)}=\frac{n}{6 n+4} \end{aligned}\)
Answer:

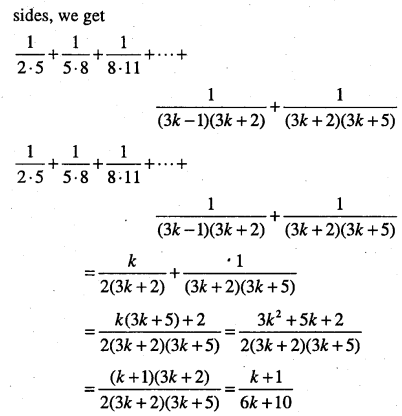
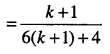
which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 10.
\(\begin{aligned} &\cfrac{1}{1 \cdot 4}+\cfrac{1}{4 \cdot 7}+\cfrac{1}{7 \cdot 10}+\cdots+\\ &\cfrac{1}{(3 n-2)(3 n+1)}=\cfrac{n}{3 n+1} \end{aligned} \)
Answer:


which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 11.
\(\begin{aligned} &\cfrac{1}{3 \cdot 5}+\cfrac{1}{5 \cdot 7}+\cfrac{1}{7 \cdot 9}+\cdots+\\ &\cfrac{1}{(2 n+1)(2 n+3)}=\cfrac{n}{3(2 n+3)} \end{aligned}\)
Answer:


which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 12.
\(\begin{aligned} &1+\cfrac{1}{1+2}+\cfrac{1}{1+2+3}+\dots+\\ &\cfrac{1}{1+2+3+\dots+n}=\cfrac{2 n}{n+1} \end{aligned} \)
Answer:

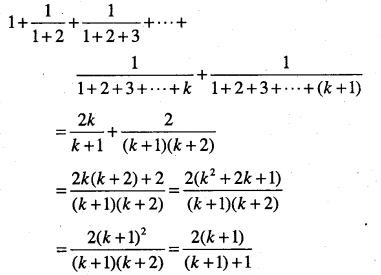
which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
![]()
Question 13.
\(\begin{aligned}&1 \cdot 3+3 \cdot 5+5 \cdot 7+\dots+(2 n-1)(2 n+1)&=\cfrac{n\left(4 n^{2}+6 n-1\right)}{3}, \text { for all } n \in N \end{aligned}\)
Answer:
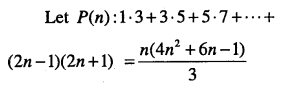

which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 14.
\(1+3+3^{2}+\cdots+3^{n-1}=\cfrac{3^{n}-1}{2} \)
Answer:

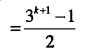
which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 15.
\(\cfrac{1}{2}+\cfrac{1}{4}+\cfrac{1}{8}+\dots+\cfrac{1}{2^{n}}=1-\cfrac{1}{2^{n}} \)
Answer:

which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 16.
\( a+a r+a r^{2}+\cdots+a r^{n-1}=\cfrac{a\left(r^{n}-1\right)}{r-1}\)
Answer:

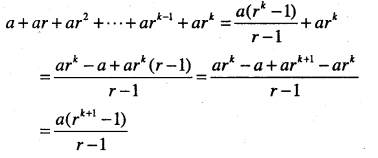
which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 17.
\( 1 \cdot 2+2 \cdot 2^{2}+3 \cdot 2^{3}+\cdots+n 2^{n}=(n-1) 2^{n+1}+2\)
Answer:

which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 18.
\( \begin{aligned} &1 \cdot 3+2 \cdot 3^{2}+3 \cdot 3^{2}+\cdots+n \cdot 3^{n}&=\cfrac{(2 n-1) 3^{n+1}+3}{4}, \text { for all } n \in N \end{aligned} \)
Answer:


which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
![]()
Question 19.
\(\left(1+\frac{1}{1}\right)\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right) \cdots\left(1+\frac{1}{n}\right)=n+1\) for all n∈N
Answer:

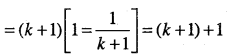
which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 20.
\( \left(1+\cfrac{3}{1}\right)\left(1+\cfrac{5}{4}\right)\left(1+\cfrac{7}{9}\right) \cdots\left(1+\cfrac{2 n+1}{n^{2}}\right)=(n+1)^{2}\)
Answer:

which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 21.
\(1^{2}+3^{2}+5^{2}+\cdots \cdot \cdot+(2 n-1)^{2}=\cfrac{n(2 n-1)(2 n+1)}{3}\)
Answer:
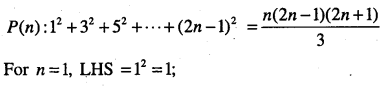

which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 22.
Prove that 2n> n for all positives integers
Answer:

Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 23.
\( 1+2+3 \cdots+n<\frac{1}{8}(2 n+1)^{2}\)
Answer:
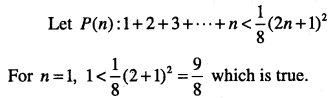

which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
![]()
Question 24.
\(1^{2}+2^{2}+3^{2}+\cdots+n^{2}>\frac{n^{3}}{3}, n \in N \)
Answer:

which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 25.
(2n + 7) < (n + 3)2
Answer:
Let P(n): (2n + 7) < (n + 3)2
For = 1, (2 + 7)<(1+ 3)2 ⇒9<16 is true.
∴ P(1) is true.
Let us assume P(k) is true for some k∈ N
i.e., (2k+ 1) < (k + 3)2
Consider 2 (k + 1) + 7 = 2k + 2 + 7
= (2k + 7) + 2
< (k: + 3)2 + 2 = k2 + 6k + 9 + 2
<(k + 4)2
∴ P(k +1) is true.
Hence, by mathematical induction, P(n) is true for all n∈N
Question 26.
72n – 32n is divisible by 4.
Answer:
Let P(n): 7n – 3n is divisible by 4.
For n = 1, P(1): 71 – 31 = 4 which is divisible by 4.
∴ P(1) is true.
Let us assume P(k) is true for some k∈N
i.e., 72n – 32n is divisible by 4.
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 27.
x2n – y2n is divisible by x+y.
Answer:
Let P(n): x2n – y2n is divisible by x + y
For n = 1, P(1): x2 – y2 is divisible by x + y, which is true.
∴ P(1) is true.
Let us assume P(k) is true for some k∈ N
i.e., x2k – y2k is divisible by x + y
Let x2k – y2k = (x + y)d, where d∈N
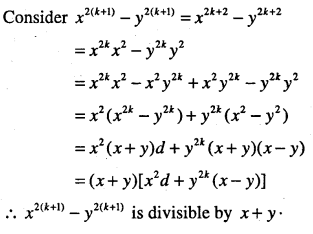
which is P(k +1)
Thus, P(k) ⇒ P(k +1).
Hence, by mathematical induction P(n) is true for all n∈N
Question 28.
102n-1 +1 is divisible by
Answer:
Let P(n): 102n-1 +1, is divisible by 11.
For n = 1, P(1):102-1 +1, is divisible by 11, which is true.
P(1) is true.
Let us assume P(k) is true for some k∈N.
i.e., 102n-1+1 is divisible by 11.
⇒102-1 +1 = 1 W, d∈N.
Consider 102(k+1)-1+1 = 102k+1 +1
= 102k-1 102+1 = (11d-1)102+1
= 11d(102)-100 + 1 = 11(100d)-99
= 11(100d-9)
∴ 102(k+1)-1 +1 is divisible by 11.
Thus, P(k) ⇒ P(k +1)
Hence, by mathematical induction, P(n) is true for all n∈N
Question 29.
32n+2 -8n-9 is divisible by 8.
Answer:
Let P(n): 32n+2 -8n-9 is divisible by 8.
For n = 1, P(1): 32+2 – 8(2) – 9 = 64 is divisible by 8, which is true.
P( 1) is true.
Let us assume P(k) is true for some k∈N
i.e., 32k+2 -8k -9 is divisible by 8.
Let 32k+2-8k-9 = 8d, d∈N ………………(1)
Consider 32(k+1)+2 – 8(k +1) – 9 = 32k+4 – 8k – 8 – 9
= 32k+2 -32-8(k-1) = (8d + 8k + 9)9-8k-17 using (1)
= (8d + 8k)9 + 81-8k-17
= 8(d + k)9 + 64-8k = 8[9(d + k) + 8-k]
which is divisible by 8.
Thus, P(k) ⇒ P(k +1)
Hence, by mathematical induction, P(n) is true for all n∈N
![]()
Question 30.
2.7n + 3.5n – 5 is divisible by 24 for all n∈N
Answer:
Let P(n): 2.7n + 3.5n – 5 is divisible by 24.
For n = 1; P(1): 2.7n + 3.5n – 5 = 24 is divisible by 24. ‘
∴ P(1) is true.
Let us assume, P(k) is true for some k∈N
i.e P(n): 2.7k + 3.5k – 5 is divisible by 24.
Let 2.7k + 3.5k – 5=24d,where d∈N
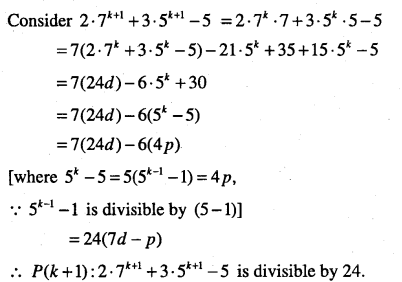
Thus, P(k)⇒P(k+ l)
Hence, by mathematical induction, P(n) is true for all n∈N
Question 31.
41n -14n is a multiple of 27.
Answer:
Let P(n): 41n -14n is a multiple of 27.
For n = 1, P(1): 41′-14′ = 47 is a multiple of 27.
∴ P(1) is true.
Let us assume P(k) is true for some k∈N

Thus, P(k)⇒P(k+ 1)
Hence, by mathematical induction, P(n) is true for all n∈N
Question 32.
n(n +1)(n + 5) is a multiple of 3.
Answer:
Let P(n): n(n + 1)(n + 5) is a multiple of 3.
For n = 1, P(1): 1(1 +1)(1 + 5) = 12 is a multiple of 3.
∴ P(1) is true.
Let us assume P(k) is true for some n∈N
i.e., P(k):k(k + 1)(k + 5) is a multiple of 3.
Let k(k + 1)(k + 5) = 3d
Consider (k + 1)(k + 2)(k + 6)
= (k + 2)(k + 1)(k + 5 + 1)
= k(k + 1)(k + 5 + 1) + 2(k + 1)(k + 5 + 1)
= k(k +1 )(k + 5) + k(k +1) + 2(k +1 )(k + 6)
Question 33.
\((a b)^{n}=a^{n} b^{n}\)
Answer:

![]()
Question 34.
(1 + x)n ≥ (1 + nx)for all natural number n, where x>-l.
Answer:
Let P(n): (1 + x)n ≥ (1 + nx), for x >-1
For n = 1; P(1): (1 + x)1 ≥ (1 + x) which is true.
Let us assume P(k) is true for some k∈N
i.e., (1 + x)k ≥ (1 + kx)
Consider (1 + x)k+1 = (1 + x)k (1 + x)
≥ (1 + kx)(1 + x)
= (l + kx + x + kx2)
≥(1 + (k + 1)x)
∵ kx2≥0.
which is P(k + 1)
Thus, P(k) ⇒ P(k +1)
Hence, by mathematical induction, P(n) is true for all n∈N