You can Download Chapter 7 Associates of Attributes Questions and Answers, Notes, 1st PUC Statistics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 1st PUC Statistics Question Bank Chapter 7 Associates of Attributes
1st PUC Associates of Attributes Question and Answers
Question 1.
What is meant by Association of Attribute? How does it differ from correlation?
Answer:
Association of attributes measures the degree of relationship between the two attributes; such as sex and literacy, literacy and employment, intelligence and employment, Beauty and Intelligence etc.
Whereas Correlation coefficient measures the degree of relationship between the variables; such as height and weight of persons, ages of husbands and wives, demand and supply of items etc.
Question 2.
How do you interpret regarding the Yule’s coefficient of association (Q)?
Answer:
- The value of this coefficient lies between ±1 (i.e., – i < Q < l).
- If Q = +1 there is perfect positive association between the attributes.
- If Q = -l there is perfect negative association (perfect dissociation) between the attributes and,
- If Q = zero the two attributes are independent.
Question 3.
What is the difference between coefficient of correlation and association of attributes?
Answer:
As we know that correlation coefficient measures the degree of relationship between the ‘ variables; such as height and weight of persons, ages of husbands and wives, demand and supply of items etc. Whereas the method of association of attributes measures the degree of relationship between the attributes; such as sex and literacy, literacy and employment, intelligence and employment etc.
![]()
Question 4.
Write the formula of Yule’s coefficient of Association.
Answer:

Question 5.
What are frequencies of first order and second orders? And mention them with their notations.
Answer:
A class having one attribute is known as the class of the first order, class of the combination two attributes as class of the second order. The total number of observations is denoted by N.
Here, N is frequency of zero order, because it has no attribute to indicate.
(A), (B), (α), (β) are called frequencies of the first order, and
(AB), (αB), (Aβ), (αβ) are called frequencies of the second order.
Question 6.
Calculate Yule’s coefficient of Association between marriage and failure of students from the following data pertaining to 525 students.
| Passed | Failed | |
| Married | 90 | 65 |
| Unmarried | 260 | 110 |
Answer:
Let A and B denotes Passed and Marriage, a and a denotes Failed and Unmarried. The 2 × 2 contingency table can be prepared as:
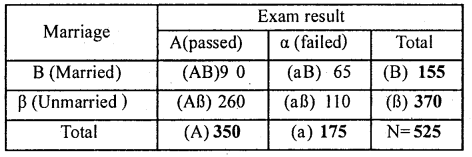
Note : In the above table figure in bold letter are adjusted figures.
Yule’s Coefficient of Association:

There exists a low degree of negative association between pass (A) and (B) marriage.
![]()
Question 7.
Eighty eight residents of a city were interviewed during sample survey are classified below, according to their smoking and tea drinking habits. Calculate Yule’s coefficient of Association and comment on its value.
| Smokers | Non -smokers | |
| Tea drinkers | 35 | 33 |
| Non tea drinkers | 8 | 12 |
Answer:
Let A and B denotes smokers and Tea drinkers, a and a denotes Failed and Unmarried. The 2 × 2 contingency table can be prepared as:
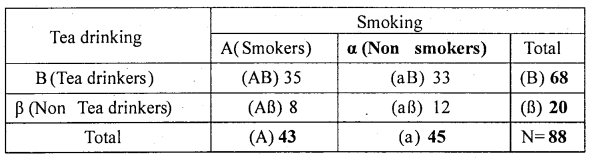
Note: In the above table figure in bold letter are adjusted figures.
Yule’s Coefficient of Association:

There exists a low degree of positive association between smoking (A) and tea drinking (B)
Question 8.
Compute Yule’s coefficient of Association from the following data.
(AB)=150, N=1000, (A)=200, (B)= 300.
Answer:
By putting the known values in the nine square tables find the unknown values to determine the Yule’s Coefficient of Association.

Note : In the above table figure in bold letter are adjusted figures.
Yule’s Coefficient of Association:
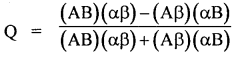

There is a high degree +ve association between the attributes.
Question 9.
Compute Yule’s co-efficient of Association from the following data.
N = 250, (Aβ) = 70, (A) = 100, (B) = 50. Ans: 0.4717
Answer:
By putting the known values in the nine square tables find the unknown values to determine the Yule’s Coefficient of Association.

Note : In the above table figure in bold letter are adjusted figures.
Yule’s Coefficient of Association:

There is a low degree +ve association between the attributes
![]()
Question 10.
Given N=500, (αβ)=280, (A)=160 and (B)=200. Calculate Yule’s coefficient of Association.
Answer:
By putting the known values in the nine square tables find the unknown values to determine the Yule’s Coefficient of Association.

Note: In the above table figure in bold letter are adjusted figures.
Yule’s Coefficient of Association:

There is a high degree +ve association between the attributes.
Question 11.
Given N=250, (AB)=40, (α)=210 and (β)=90
Calculate Yule’s coefficient of Association. Ans: 1
Answer:
By putting the known values in the nine square tables find the unknown values to determine the Yule’s Coefficient of Association.
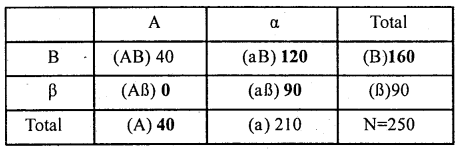
Note : In the above table figure in bold letter are adjusted figures.
Yule’s Coefficient of Association:
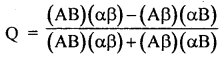

![]()