Students can Download Basic Maths Exercise 11.1 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 11 Linear Programming Problems Ex 11.1
Part – A
2nd PUC Basic Maths Linear Programming Problems Ex 11.1 Four Marks Questions with Answers
Question 1.
Smaran being a manufacturer produces nuts and bolts for industrial machinery. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts while it takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of ₹ 2.50 per package on nuts and 1 per package on bolts. Form a linear programming problem to maximize his profit, if he operates each machine for at most 12 hours a day,
Answer:

Let the number of units of nuts x & bolts be y it takes 1 hour on machine A for a nut and 3 hours on machine 13 for a nut maximum time available for machine A is 12 hours.
∴ x + 3y ≤ 12
3x + y ≤ 12
Negative units cannot be produced: x, y ≥ 0 our objective is to maximum profit the LPP is Maximize = 2.5 x + y subject to
x + 3y ≤ 12
3x + y ≤ 12
and x ≥ 0, y ≥ 0
![]()
Question 2.
Vishal consumes two types of food, A and B everyday to obtain minimum 8 units of protein, 12 units carbohydrates and 9 units of fat which is his daily requirements. 1kg of food A contains 2, 6, 1 units of protein, carbohydrates and fat respectively. 1 kg of food B contains 1, 1 and 3 units of protein, carbohydrates and fat respectively. Food A cost ₹ 8 per kg and food B cost ₹ 5 per kg. From an L.P.P. to find how many kilogram of each food should he buy daily to minimize his cost of food and still meet minimal nutritional requirements.
Answer:

Let the units of food A be x & food B be y
Minimize z = 8x + 5y subject to the constraints
2x + y ≥ 8
6x + y ≥ 12
x + 3y ≥ 9
x, y ≥ 0 : x – y ≥ 0
Question 3.
Archana, a dietician wishes to mix two types of foods F1 and F2 in such a way that the vitamin contents of the mixture contains at least 6 units of vitamin A and 8 units of vitamin B. Food F1 contains 2 units/kg of vitamin A and 3 units/kg of vitamin B while food F2 contains 3 units/kg of vitamin A and 4 units/kg of Vitamin B. Food F1 costs ₹50 per kg and food F2 costs ₹ 75 per kg. Formulate the problem as L.P.P. to minimize the cost of the mixture.
Answer:

Let the units of food F, be x and food F, be y minimize z = 50x + 75y subject to the restrictions
2x + 3y ≥ 6
3x + 4y ≥ 8
x,y ≥ 0
![]()
Question 4.
A furniture maker Jatin has 6 units of wood and 28 hours of free time in which he will make decorative screens. Two models have sold well in the past, so he will restrict himself of those two. He estimates that | model 1 requires 2 units of wood and 7 hours of time. Model 2 requires 1 units of wood and 8 hours of time. The prices of the models are ₹ 120 and ₹ 80 respectively. Formulate LPP to determine how many screens of each model should the furniture maker assemble if the wishes to maximize his sales revenue.
Answer:
Let the number of units of model I be x and model II be y

Maximize z = 120 x + 80 y subject to the constraints
2x + y ≥ 6
7x + 8y ≥ 8
x, y ≥ 0
![]()
Question 5.
A firm owned by Sheshnag manufactures two types of products A and B and sell them at a profit of ₹ 2 on type of A and 3 on type B. Each product is processed on machines M1 and M2. Type A requires one minute of processing time on M1 and two minutes on M2. Type B requires one minute of time on M1 and one minute on M2. The machine M1 is available for not more than 6 hours 40 minutes while M2 is available for 10 hours during any working day. Formulate the L.P.P. in order to find how many products of each type, should the firm produce each day so that profit is maximum.
Answer:
Let the number of units of product A bex & product B be y
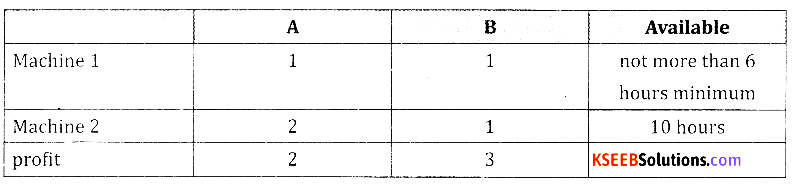
Maximize z = 2x + 3y subject to the constraints
[6 hrs + 40 minutes 360 minutes + 40 minutes = 400 minutes]
x + y ≤ 400
2x + y ≤ 600
x, y ≥ 0
Question 6.
Shreya company produces 2 types of shoes A and B. A is of superior type and B is of ordinary type. Each
shoe of the first kind requires thrice as much time as the second kind. If all shoes are the second kind only, the company can produce a total of 650 pairs a day. Only a maximum of 150 pairs of the first kind and 400 of the second kind can be sold per day. If the profit per pair of the first kind is ₹ 400 and per pair of the second kind is ₹ 105. Find the optimal products mix to be produced to maximize the profit by formulating on L.P.P. model.
Answer:
Let the number of units of shoe A be x and shoe B be y, time taken by shoe A is hours & time taken by shoe B is 1 hour company can produce 650 pairs per day
∴ 3x + y ≤ 650 Similarly maximum of 150 pairs of shoe A can be produced i.e x ≤ 150 and 400 of shoe B can be sold i.e. y ≤ 400 Maximize z = 400x + 105y subject to the constraints
3x + y ≤ 650
x ≤ 150
y ≤ 400
x ≥ 0,y ≥ 0
![]()
Question 7.
Producer Rahul has 50 and 85 units of labour and capital respectively which he can use to produce two
types of goods A and B. To produce one unit of A, 1 unit of labour and 2 units of capital are required. Similarly 3 units of labour and 2 units of capital is required to produce 1 unit of B. If A and B are priced at ₹ 100 and ₹ 150 per unit respectively, how should the producer use his resources to maximize the total revenue. Formulate the L.P.P. to maximize his total revenue?
Answer:
Let the units of product A be x and product B be y

Maximize z = 100 x + 150 y subject to the restrictions
x + 3y ≤ 50
2x + 2y ≤ 85
x,y ≥ 0
![]()
Question 8.
Nikhil pesticide company must produce 200 kg mixture consisting of chemicals A and B daily. A cost ₹ 3 per kg and B cost ₹ 8 per kg. Maximum 80 kg of chemical A and atleast 60 kg, of chemical B should be used. Formulate L.P.P. model to minimize the cost.
Answer:
Let the units of A be x and B be y maximum 80 kg of chemical A used x ≤ 80
At least 60 kg of chemical B is used y ≥ 60 Company should produce 200 kg x + y ≤ 200
Minimise z = 3x + 8y subject to the constraints
X + y ≤ 200
x ≤ 80, y ≥ 60
x, y ≥ 0.