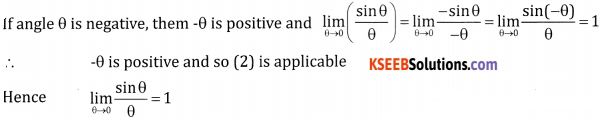Students can Download Basic Maths Exercise 17.5 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Basic Maths Question Bank Chapter 17 Limit and Continuity of a Function Ex 17.5
Part – A
2nd PUC Basic Maths Limit and Continuity of a Function Ex 17.5 Two or Three Marks Questions and Answers
Question 1.
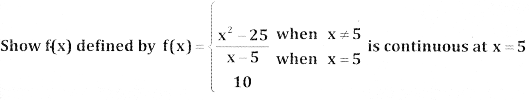
Answer:
Also f(x) at x = 5 is 10; i.e, f(5) = 10
![]()
∴ the function f(x) is continuous at x = 5
Question 2.
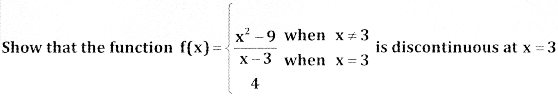
Answer:

![]()
Question 3.
Define f(0) so that f(x) = \(\frac{x}{1-\sqrt{1-x}}\) become continuous at x = 0
Answer:

Also f(x) at x = 0 is 2
i.e f(x) = f(0) = 2
since f is continuous at x = 0.
Question 4.
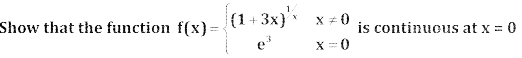
Answer:
![]()
Also f(x) at x = 0 is e3 i.e f(0) = e3
![]()
∴ f(x) is continuous at x = 0
Question 5.
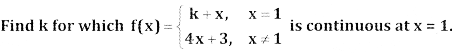
Answer:
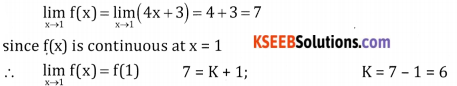
![]()
Question 6.
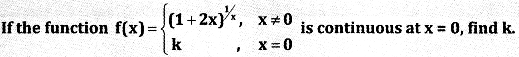
Answer:
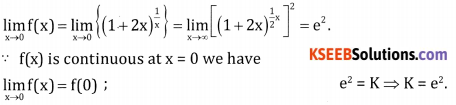
Question 7.
![]()
Answer:
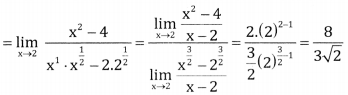
Question 8.
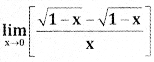
Answer:

![]()
Question 9.
![]()
Answer:

Question 10.
![]()
Answer:
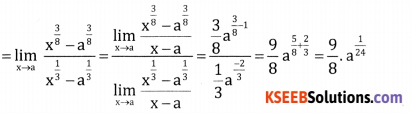
![]()
Part – C
2nd PUC Basic Maths Limit and Continuity of a Function Ex 17.5 Five Marks Questions and Answers
Question 1.
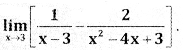
Answer:
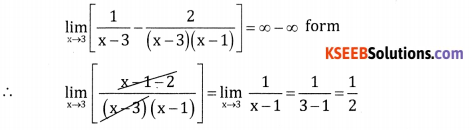
Question 2.
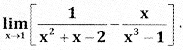
Answer:

![]()
Question 3.
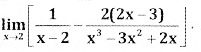
Answer:

Question 4.
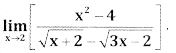
Answer:

![]()
Question 5.
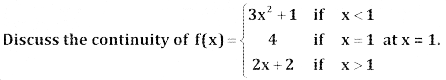
Answer:

Question 6.
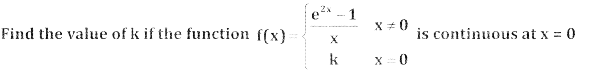
Answer:

![]()
part – B
2nd PUC Basic Maths Limit and Continuity of a Function Ex 17.5 Six Marks Questions and Answers
Limits Theorems
Question 1.
prove that \(\lim _{x \rightarrow a} \frac{x^{n}-a^{n}}{x-a}=n a^{n-1}\) for all values of n
Answer:
Case – 1 : Let n be a positive integer.
xn – an = (x – a)(xn -1 + xn-2 . a + xn-3 . a2 + ……. + an-1

Case – 2: Let n be a positive integer
Put n = -m, m > 0

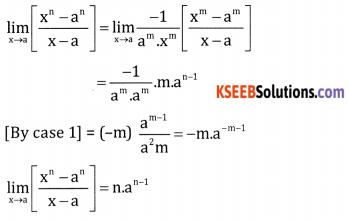
Case – 3: Let n = p/q where p and q are integers and q ≠ 0

![]()
Question 2.
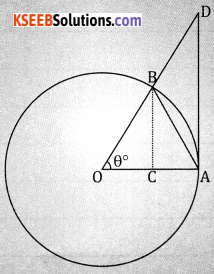
![]()
Answer:
Let ‘0’ the centre of unit circle, assume that θ is measured in positive radians
![]()
Fromn the figure, we have area of ∆AOB = area of sector AOB = area of ∆AOD
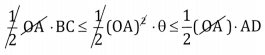
∴ Area of sector = \(\frac { 1 }{ 2 }\) (radius)2 × angle in radians
From the triangle DOA, tan θ = \(\frac{\mathrm{DA}}{\mathrm{OA}}\) ∴DA = rtan θ
From the triangle BOC, sin θ = \(\frac{\mathrm{BC}}{\mathrm{OB}}\) ∴ BC = rsin θ
(1) becomes
⇒ BC ≤ θ ≤ DA
⇒ sin θ ≤ θ ≤ tan θ
Dividing by sin θ