2nd PUC Basic Maths Question Bank Chapter 7 Ratios and Proportions Ex 7.3

Students can Download Basic Maths Exercise 7.3 Questions and Answers, Notes Pdf, 2nd PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Basic Maths Question Bank Chapter 7 Ratios and Proportions Ex 7.3

Part – A

2nd PUC Basic Maths Ratios and Proportions Ex 7.3 Three Marks Questions and Answers ( 3 × 4 = 12)

Question 1.
If ₹ 150 maintains a family of 4 persons for 30 days. How long 7600 maintain a family of 6 persons?
Answer:

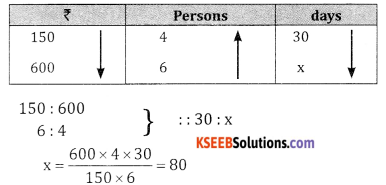
Question 2.
300 workers can finish a work in 8 days. How many workers will finish the same work in 5 days.
Answer:

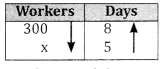
Workers and days are in inverse proportion 300 : x = 5 : 8
x = \(\frac{300 \times 8}{5}\) = 480 workers

Question 3.
5 carpenters can earn ₹540 in 6 days working 9 hours a day. How much will 8 carpenters can earn in 12 days working 6 hours a day?
Answer:

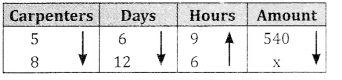
Days and amount are in direct proportion, hours and amount are in direct proportion

Question 4.
A mixture contains milk and water in the ratio 6:1 on adding 5 litres of water, the ratio of milk and water becomes 7 : 2, find the quantity of milk in the original mixture.
Answer:
Quantity of milk is 6x and water is 1x, 5 liters of water is added, the new ratio is 7:2
\(\frac{6 x}{x+5}=\frac{7}{2}\)
12x = 7x + 35 ⇒ 5x = 35
x = 7
The quantity of milk is 6(x) = 6 (7) = 42

Part – B

2nd PUC Basic Maths Ratios and Proportions Ex 7.3 Five Mark Questions and Answers 

Question 1.
A jar contains two liquids X and Y in the ration 7:5. When 6 litres of the mixture is drawn and the jar in filled with the same quantity of Y, the ratio of Xand Y becomes 7:9. Find the quantity X in the jar initially,
Answer:
Let quantity of liquid X is 7x and Y is 5x 6 liters of the mixture is drawn.
i.e.,\(\frac{7 \times 6}{12}=\frac{7}{2}\) litres of X is removed
\(\frac{5 \times 6}{12}=\frac{5}{2}\) litres of Y is removed
∴ The remaining quantity of X and Y is 7x – \(\frac{7}{2}\) and 5x –\(\frac{5}{2}\) respectively.
6 litres of Y is added to get ratio 7:9.

Question 2.
Two taps fill a cistern separately in 20 minutes and 40 minutes respectively and a drain pipe can drain off 30 litres per minute. If all the three pipes are opened, the cistern fills in 72 minutes what is the capacity of the cistern?
Answer:
Time taken by tap A is 20 min
∴ \(\frac{1}{20}\)b of the Cistern is filled by tap A
Similarly \(\frac{1}{40}\) of the Cistern is filled by tap B
Both the taps can fill \(\frac{1}{20}+\frac{1}{40}=\frac{3}{40}\)
“204040 A drain tap can drain 30 liters per minute the cistern is filled in 60 minute.

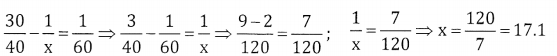
The drain tap can drain in 17 minutes in 1minute it drains 30 litres
In 17 minutes it drains 30 × 17litres
∴ The capacity of the cistern = 510 litres

Question 3.
If ten persons can do a job in 60 days. In how many days can twenty persons do the same job?
Answer:

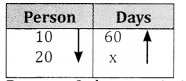
Persons & days are in inverse proportion
∴ 10:20 = x : 60
X= \(\frac{60 \times 10}{20}\) = 30days 20

Question 4.
A can do a piece of work in 20 days, B in 30 days and C in 60 days. All of them began to work together. However, A left the job after 6 days and B quit work 6 days before the completion of work. How many days
did the work last?
Answer:
In 1 day the work done by A, B & C is

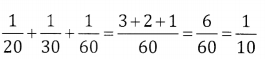
In 6 days the work done is \(\frac{6}{10}=\frac{3}{5}\)
Remainin work is \(1-\frac{3}{5}=\frac{2}{5}\) of the work
Let the number of days to complete the work be x.C does \(\frac{x}{60}\) of the work & B does \(\frac{x-6}{30}\) of the work in x days

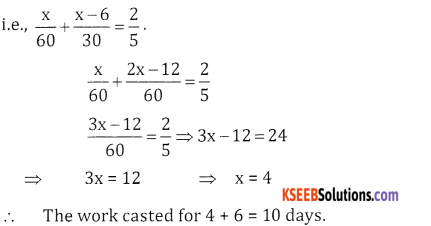
Question 5.
8 men and 16 women can finish a job in 6 days | but 12 men & 24 women can finish it in 8 days. How many days will 26 men and 20 women take to finish the job?
Answer:
8 men & 16 women can finish a Job in 6 days
∴ In 1 day the work done is of 48men and 96 women.
12 men & 24 women can finish a job in 8 days. In 1 day the work done is of 96 men & 192 women.
∴ 48 men + 96 women = 96 men + 192 women
26M + 20W = 52W + 20W = 72W
Let the required number of days be x.
192 : 72 = x : 5
X = \(\frac{192 \times 5}{72}=\frac{45}{3}\) = 15 days

Question 6.
4 men and 12 boys can do a piece of work in 5 … days by working 8 hours per day. In how many days 2 men & 4 boys can do the same piece of work working 12 hours a day.
Answer:
Given 4 m = 12 B
1 m = 3 B
2men & 4 boys = 6 boys + 4 boys = 10 boys

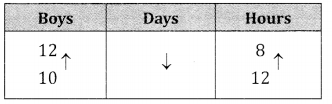
Boys & days are in inverse proposition days & hours are in inverse proportion.
∴ 10 : 12 :: 5 : x 12 : 8
x = \(\frac{12 \times 8 \times 5}{10 \times 12}=\) = 4days.

Question 7.
A railway train 100 metres long is running at the speed of 30 kmph. In what time will it pass (i) a man standing near the line (ii) a bridge 100 metres long?
Answer:
d = 100m Speed = 30km ph
Speed = \(\frac{\mathrm{d}}{\mathrm{t}}\)

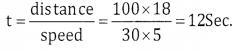
Length of the bridge is 100m
d = 100 + 100 = 200
t = \(\frac{200 \times 18}{30 \times 5}\) = = 24 Sec.

Question 8.
The driver of car is traveling at a speed of 36 kmph and spots a bus 80 metres ahead of him. After 1 hour the bus is 120 metres behind the car. What is the speed of the bus?
Answer:
Speed of the car = 36 kmph
Speed of the bus = x kmph
Relative speed = (36 – x) kmph
Distance = 200m
Bus by 120m
∴ t = \(\frac{200}{36-x}\)
1 = \(\frac{200}{(36-x) 1000}\)
36 – x = 0.2
36 -0.2 = x
x = 35.8
∴ Speed of the bus is 35.8 kmph.