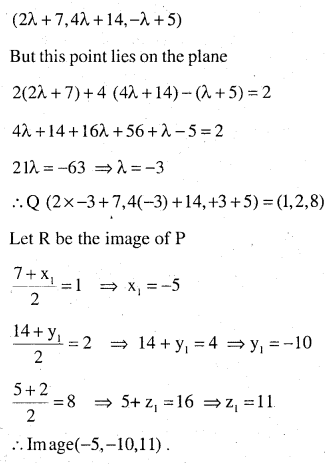2nd PUC Maths Question Bank Chapter 11 Three Dimensional Geometry Miscellaneous Exercise

Students can Download Maths Chapter 11 Three Dimensional Geometry Miscellaneous Exercise Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 2nd PUC Maths Question Bank Chapter 11 Three Dimensional Geometry Miscellaneous Exercise

Question 1.
Show that the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5, – 1), (4, 3, – 1).
Answer:
Dr’s of the line joining the origin to the point (2,1,1 )is (2 – 0, 1 – 0, 1 – 0)
∴ (2, 1,1)
Dr’s of the line joining (3, 5,-1) and (+4, 3,-1)
is (4 – 3 ,3 – 5,1 – 1)  (1, -2, 0)
1 x 2 – 2 x 1 + 1 x 0 = 0
hence a₁b₁ + a₂b₂ + a₃b₃ = 0
∴ lines are perpendicular.

Question 2.
If l₁, m₁ , n₁ and l₂, m₂, n₂ are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are
m₁n₂ – m₂n₁, n₁l₂ – n₂l_p l₁m₂ – l₂m₁
Answer:
The given lines are respectively parallel to
\(\bar{a}_{1}=1, \bar{i}+m_{1} \bar{j}+n_{1} \bar{k} \text { and } \bar{a}_{2}=1_{2} \bar{i}+m_{2} \bar{j}+n_{2} \bar{k} \bar{a}_{1} \times \bar{a}_{2}\) is a vector which is normal to both \(\bar { a } _{ 1 }\quad and\quad \bar { a } _{ 2 }\) and is of magnitude unity.

Question 3.
Find the angle between the lines whose direction ratios are
(a, b, c) and (b – c, c – a, a – b.)
Answer:

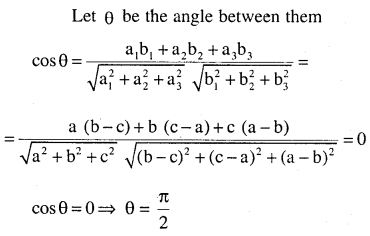
Question 4.
Find the equation of a line parallel to x-axis and passing through the origin.
Answer:
Dc’s of x-axis (1, 0, 0)
Dc’s of any line parallel to x-axis is also (1,0,0).
The required equation passes through (0,0,0) and having Dc’s (1, 0,0) is
\(\frac{x-0}{1}=\frac{y-0}{0}=\frac{z-0}{0}\)

Question 5.
If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (- 4, 3, – 6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.
Answer:
Dr’s of AB = (3, 3, 4), Direction CD = (6,6, 8)
\(\frac{3}{6}=\frac{3}{6}=\frac{4}{8} \) Dr’s are proportional. Hence they are parallel
∴ Angle between them = 0°

Question 6.
If the lines
\(\frac { x-1 }{ -3 } =\frac { y-2 }{ 2k } =\frac { z-3 }{ 2 } \quad and\quad \frac { x-1 }{ 3k } =\frac { y-1 }{ 1 } =\frac { z-6 }{ -5 } \)
are perpendicular, find the value of k.
Answer:
Here Dr’s of the lines are (-3, 2k, 2) and (3k, 1,-5) .
since the lines are perpendicular
-3 x 3k + 2k x 1 x 2 x -5 = 0
\(-9 k+2 k-10=0 \Rightarrow-7 k=10 \Rightarrow k=\frac{-10}{7}\)

Question 7.
Find the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane \(\overrightarrow{\mathbf{r}} \cdot(\hat{\mathbf{i}}+2 \hat{\mathbf{j}}-5 \hat{\mathbf{k}})+9=\mathbf{0}\)
Answer:
Dr’s of the normal to the plane is (1,2,-5)
Since the required line is ‘⊥’ to the plane, these Dr’s are equal.
∴ Dr’s of the line (1,2, -5) and passing through (2,3)
∴ \(\text { Line is } \frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{-5}\)
hence vector equation of the line is
\(\overline { { r } } =\overline { { a } } +\lambda \overline { { b } } \quad \overrightarrow { { r } } =(\overrightarrow { { i } } +2\overrightarrow { { j } } +3\overrightarrow { { k } } )+\lambda (\overrightarrow { { i } } +2\overrightarrow { { j } } -5\overrightarrow { { k } } )\)

Question 8.
Find the equation plane passing (a,b,c) and parallel to the plane
\(\overrightarrow{\mathbf{r}}\cdot(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}})=2\)
Answer:
The required plane is parallel to
\(\overrightarrow{\mathbf{r}}\cdot(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}})\) hence Dr’s of the normal to the plane is (1, 1, 1) and through the points
(a, b, c)
∴ its equation is \((\overline{\mathbf{r}}-\overline{\mathbf{a}}) \cdot \hat{\mathbf{n}}=0\)
(x – a) x 1 + (y – b) x 1 x (z – c).1 = 0
∴ x + y + z = a + b + c.

Question 9.
Find the shortest distance between lines
\(\begin{matrix} & \overrightarrow { { r } } =6\hat { { i } } +2\hat { { j } } +2\hat { { k } } +\lambda (\hat { { i } } -2\hat { { j } } +2\hat { { k } } ){ and } \\ & \overrightarrow { { r } } =-4\hat { { i } } -\hat { { k } } +\mu (3\hat { { i } } -2\hat { { j } } -2\hat { { k } } ) \end{matrix}\)
Answer:

Question 10.
Find the coordinates of the point where the line through (5, 1, 6) and (3, 4,1) , crosses the YZ- plane.
Answer:
Equation of line through (5, 1, 6) and (3,4,1) is

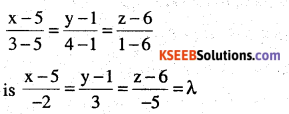
∴ Any points on the line

Question 11.
Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the ZX – plane.
Answer:

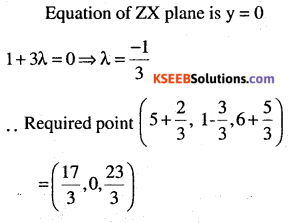
Question 12.
Find the coordinates of the point where the line through (3, – 4, – 5) and (2, – 3,1) crosses the plane 2x + y + z = 7.
Answer:
Equation of plane through (3, -4, -5) and
\((2,-3,1) \text { is } \frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}\)
any point on the line (3 – λ, -4 + λ, -5 + 6λ) but this point lies on the plane 2x + y + z = 7 6 – 2λ,-4 + λ -5 + 6λ = 7
+5λ = +10 ⇒ λ = +2
∴ Required point is (1, -2,7).

Question 13.
Find the equation of the plane passing through the point (- 1, 3, 2) and perpen­dicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.
Answer:
Let the equation of plane through (-1,3, 2) be
A (x + 1) + B (y – 3) + C (z-2) = 0 → (1)
But this plane is ‘⊥’ to both given planes
A + 2B + 3C = 5 and → (2)
3A + 3B + C = 0 → (3)
solving (1), (2) and (3)

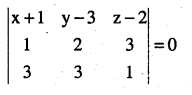
⇒ (x +1)(-7) – (y – 3)(-8) + (z – 2)(-3) = 0
7x – 8y + 3z + 25 = 0
OR
Equation of plane through (x₁, y₁, z₁) and is perpendicular a₂x + a₂y + a₃z = c₁
b₁x + b₂y + b₃z = c₂ is of the

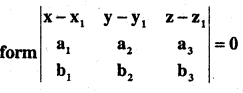
Question 14.
If the points (1,1, p) and (- 3,0,1) be equidistant from the plane \(\overrightarrow{\mathrm{r}} \cdot(3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}-12 \hat{\mathrm{k}})+13=0 \) then find the value of p.
Answer:
The equation of plane is 3x + 4y – 12z + 13 =0 distances from (1, 1, p) and (-3, 0, 1) are

Question 15.
Find the equation of the plane passing through the line of intersection of the planes
and parallel to x-axis.
Answer:
Equation of planes are x + y + z – 1= 0 and 2x + 3y – z + 4 = 0 any plane through their enter section is of the form.
(x + y + z – 1)+λ (2x + 3y – z + 4) = 0
(1+ 2λ) x + y(1+3λ) + z(1- λ) – 1 + 4λ) = 0
but this plane is parallel to x-axis whose direction are (1,0,0)

Question 16.
If O be the origin and the coordinates of P be (1, 2, – 3), then find the equation of the plane passing through P and perpendicular to OP.
Answer:
Directions of OP = (1, 2, -3)
∴ Equation of plane through (1, 2, -3) and
Dr’s of normal is (1,2, -3) is A (x – x₁) + B (y – y₁) + C (z – z₁) = 0
1 (x – 1) + 2(y – 2) -3(z + 3) = 0
x – 1 + 2 (y – 2) -3 (z + 3) = 0
x + 2y – 3z – 14 = 0

Question 17.
Find the equation of the plane which contains the line of intersection of the planes \(\overrightarrow{\mathrm{r}} \cdot(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})-4=0, \quad \overrightarrow{\mathrm{r}} \cdot(2 \hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}})+5=0 \) and which is perpendicular to the plane \(\overrightarrow{\mathrm{r}} \cdot(5 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-6 \hat{\mathrm{k}})+8=0\)
Answer:
(x + 2y + 3z – 4) + λ (2x + y – z + 5) = 0
x(1+2λ)+ λ (2+λ) +z (3 – λ) – 4 + 5 λ =0
the given plane is ‘⊥’ to the plane

Question 18.
Find the distance of the point (- 1, – 5, -10) from the point of intersection of the line
\(\overrightarrow { { r } } =2\hat { { i } } -\hat { { j } } +2\hat { { k } } +\lambda (3\hat { { i } } +4\hat { { j } } +2\hat { { k } } )and\quad plane\quad \overrightarrow { { r } } \cdot (\hat { { i } } -\hat { { j } } +\hat { { k } } )=5\)
Answer:

Question 19.
Find the vector equation of the line passing through (1,2,3) and parallel to the planes
\(\overrightarrow{\mathbf{r}} \cdot(\hat{\mathbf{i}}-\hat{\mathbf{j}}+2 \hat{\mathbf{k}})=5 \text { and } \overrightarrow{\mathbf{r}} \cdot(3 \hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}})=6\)
Answer:
Equation of the line through (1,2,3) is \(\frac{x-1}{a}=\frac{y-2}{b}=\frac{z-3}{c}\) but this is plane is parallel to the plane
x – y + 2z = 5 and 3x + y + z = 6
1 x a – 1 x b + 2 x c = 0 ⇒ a – b + 2c = 0
and 3 x a + 1 x b + 1 x c = 0

Question 20.
Find the vector equation of the line passing through the point (1, 2, – 4) and perpendicular to the two lines:
\(\begin{aligned}&\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7} \text { and }\\&\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}\end{aligned}\)
Answer:

\(\overline{\mathbf{r}}=(\overrightarrow{\mathbf{i}}+2\overrightarrow{\mathrm{j}}-4 \overline{\mathbf{k}})+\lambda(2 \overrightarrow{\mathrm{i}}+3 \overrightarrow{\mathrm{j}}+6 \overrightarrow{\mathrm{k}})\)

Question 21.
Prove that if a plane has the intercepts a, b, c and is at a distance of p units from the origin then \(\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=\frac{1}{p^{2}}\)
Answer:

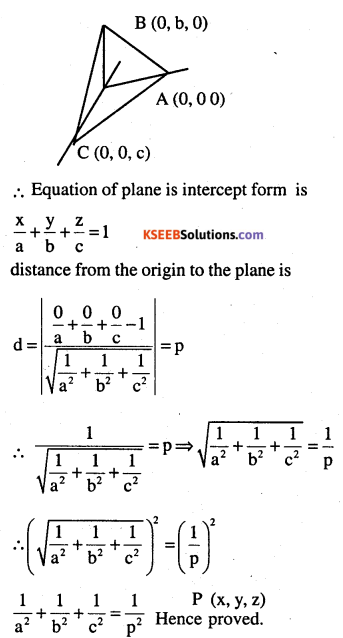
Choose the correct answer in exercise 22 and 23.

Question 22.
Distance between the two planes: 2x + 3y + 4z = 4 and 4x + 6y + 8z = 12 is
(A) 2 units
(B) 4 units
(C) 8 units
(D) \(\frac{2}{\sqrt{29}} \text { units }\)
Answer:

Question 23.
The planes: 2x – y + 4z = 5 and 5x – 2.5y + 10z = 6 are
(A) Perpendicular
(B) Parallel
(C) passes through \(\left(0,0, \frac{5}{4}\right)\)
Answer:

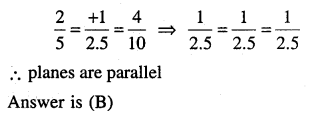
2nd PUC Maths Three Dimensional Geometry Miscellaneous Exercise Extra Questions and Answers

Question 1.
Write the distance of the following plane from the origin, 2x-y + 2z + 1 = 0 (CBSE  2010)
Answer:

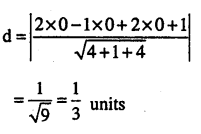
Question 2.
Find the points on the line \(\frac{x+2}{3}=\frac{y+1}{2}=\frac{z-3}{2}\) at a distance of 5 units from the points (1,3,5) (CBSE  2010)
Answer:

Question 3.
Find the distance of the point P (6,5,9) from the plane determined by A (3, -1, 2) B (5, 2, 4) and C (-1, -1, 6) (CBSE 2010)
Answer:
Equation of plane inn three point form is

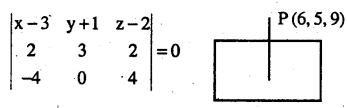
(x – 3) 12 – (y + 1) (8 + 8) + (z – 2) (12) = 0
12x – 36 – 16y – 16 + 12z – 24 = 0
12x – 16y + 12z – 76 = 0
3x – 4y + 3z -19 = 0

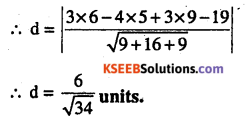
Question 4.
Write the dc’s of the line joining the points (1,0, 0) and (0,1,1) (CBSE 2011)
Answer:
Direction ratios = (-1,1,1)

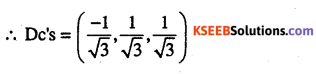
Question 5.
Write the vector equation of the line (CBSE 2011)
\(\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}\)
Answer:
The given lines passes through (5, -4,6)
and is parallel to the vector
\((3 i+7 j+2 \bar{k}) is\)

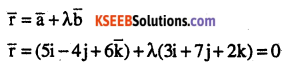
Question 6.
Find the distance of a point 3x – 4y + 122 = 3 from the origin (CBSE 2012)
Answer:

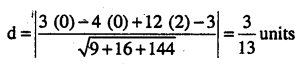
Question 7.
Find the co-ordinate of the foot of ⊥^r and the perpendicular distance of the point P (3, 2,1) from the plane 2x -y + z + 1 = 0. Find also the image of the point in the plane (CBSE 2011)
Answer:
Direction of a normal to the plane (2, -1, 1)
Let Q be the foot of ⊥ from p to the plane
Normally line is parallel to plane PQ

Equation of PQ =
\(\frac{x-3}{2}=\frac{y-2}{-1}=\frac{z-1}{1}\)
Any point on this line is (2λ + 3, -λ + 2, λ +1)
If this point is Q which lies on the plane

Question 8.
Find the equation of the plane passing through the point P (1,1,1) and containing the line \(\overline{\mathbf{r}}=(-3 \mathbf{i}+\mathbf{j}+5 \overline{\mathbf{k}})+\lambda(\mathbf{3} \mathbf{i}-\mathbf{j}-\mathbf{5} \overline{\mathbf{k}})\). Also show that the plane contains the line
Answer:
\(\overline{\mathbf{r}}=(-3 \mathbf{i}+\mathbf{j}+5 \overline{\mathbf{k}})+\lambda(\mathbf{3} \mathbf{i}-\mathbf{j}-\mathbf{5} \overline{\mathbf{k}})\)
Equation of plane through the point (1,1,1) is of the form
A (x – 1) + B (y – 1) + C (z – 1) = 0 .
This plane containing the line

(x – 1) (4) – (y – 1) (20 – 12) +(z – 1) (4)
4x – 4 – 8y + 8 + 4z – 4 = 0
4x-8y + 4z = 0 ⇒ x -2y + z = 0
since the point (1,-2, -5) lies on the plane
x – 2y + z = 0 as 1 x 1 – 2x – 2 – 5 = 0 and
\(\left( i-2j-5\bar { k } \right) \cdot \left( i-2j\quad +\bar { k } \right) =1+4-5=0\) the plane x – 2y +z = 0 contains the lines
\(\overline{\mathbf{r}}=(-i+2 j+5 \overline{\mathbf{k}})+\mu(\mathbf{i}-2 j-5 \overline{\mathbf{k}})\)

Question 9.
Find the points on the line
\(\frac{x+2}{3}=\frac{y+1}{2}=\frac{z-3}{2}\) at a distance of 5 units from the points (1,3,3) (CBSE 2011)
Answer:
Any point on the line.

Question 10.
Find the distance of the point P (6, 5, 9) from the plane determined by the points A (3, -1, 2), B (5, 2, 4) and C (-1, -1, 6) (CBSE 2011)
Answer:

Question 11.
Find the shortest distance between the following lines whose vector equals
\(\begin{aligned}&\overline{\mathbf{r}}=(1-\mathbf{t}) \mathbf{i}+(\mathbf{t}-\mathbf{2}) \mathbf{j}+(\mathbf{3}-\mathbf{2} \mathbf{t}) \overline{\mathbf{k}} \text { and }\\&\overline{\mathbf{r}}=(\mathbf{s}+\mathbf{1}) \mathbf{i}+(2 \mathbf{s}-\mathbf{1}) \mathbf{j}-(2 \mathbf{s}+\mathbf{1}) \overline{\mathbf{k}}\end{aligned}\)
Answer:

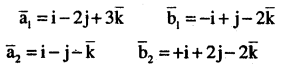
Question 12.
If the lines
\(\frac { x-1 }{ -3 } =\frac { y-2 }{ -2k } =\frac { z-3 }{ 2 } ,\frac { { x }-{ 1 } }{ { K } } =\frac { { y }-{ 2 } }{ { 1 } } =\frac { { z }-{ 3 } }{ { 5 } } { are }\perp ^{ { r } },{ find\quad }{ K }\)
Answer:
Directions of tines are (-3, -2K, 2) and (K, 1,5)
since lines are ⊥^r a₁b₁ + a₂b₂ + a₃b₃ = 0
-3 x K – 2K x 1 + 2 x 5 = 0
-3K – 2K + 10 = 0, -5K = -10, K =2

Question 13.
Find the length and the foot of the ⊥^r from the point P (7, 14, 5) to the plane 2x + 4y – z = 2. Also find the image of the point P in the plane. (CBSE 2012)
Answer:
Direction of the normal to the plane is (2, 4,-1)

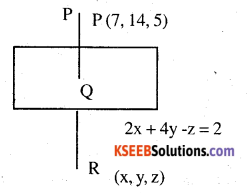
∴ Equation of PQ through (7,14,5) and parallel to a vector whose Directions are (2, 4, 1) is \(\frac{x-7}{2}=\frac{y-14}{4}=\frac{z-5}{-1}\)