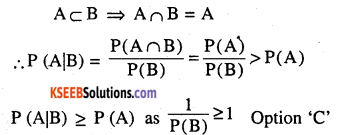Students can Download Maths Chapter 13 Probability Ex 13.3 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 13 Probability Ex 13.3
2nd PUC Maths Probability NCERT Text Book Questions and Answers Ex 13.3
Question 1.
An urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the urn and then a ball is drawn at random. What is the probability that the second ball is red ?
Answer:
In the first draw the ball may be red or black
(1) If red ball is drawn, 2 more red balls are put and then draw a red ball
(2) If black ball is drawn 2 more black ball is put and then again draw a red ball
∴ Required probability is
\(\frac{5}{10} \times \frac{7}{12}+\frac{5}{10} \times \frac{5}{12}=\frac{60}{120}=\frac{1}{2}\)
![]()
Question 2.
A bag contains 4 red and 4 black balls , another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that the ball is drawn from the first
Answer:
Let E1 : The first bag is selected
E2 : The second bag is selected
A : The ball is red

Question 3.
Of the students in a college, it is known that 60% reside in hostel and 40% are day scholars (not residing in hostel). Previous year result report that 30% of all students who reside in hostel attain A grade and 20% of day scholars attain A grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an A grade, what is the probability that the student is a hostlier ?
Answer:
E1 : Student is a hostler
E2 : Student is a day scholar
A : student has an A grade
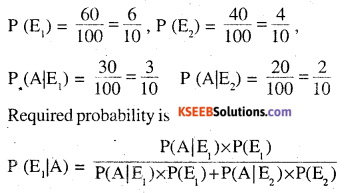

Question 4.
In answering a question on a multiple r. choice test, a student either knows the answer or guesses. Let \(\frac{3}{4}\) be the probability that he knows the answer and \(\frac{1}{4}\) be the probability that he guesses.Assuming that a student who guesses at the answer will be correct with probability \(\frac{1}{4}\) . What is the probability that the student knows the answer given that he answered it correctly ?
Answer:
E1: student knows the answer
E2 : student guesses the answer
A : Answer is correct
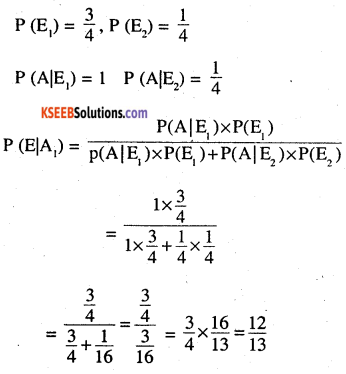
![]()
Question 5.
A laboratory blood test is 99% effective in detecting a certain disease when it is in
fact, present. However, the test also yields a false positive result for 0.5% of the healthy person tested (i.e. if a healthy person is tested, then, with probability 0.005, the test will imply he has the disease). If 0.1 percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive ?
Answer:
E1: person has the disease
E2: person is healthy
A : Test is positive

Question 6.
There are three coins. One is a two headed coin (having head on both faces), another is a based coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin?
Answer:
E1 : 1st coin is chosen
E2 2nd coin is chosen
E2: 3rd coin is chosen
Let ‘A’ be the even that shows head
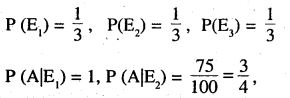

![]()
Question 7.
An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accidents are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?
Answer:
E1: Insured person is scooter driver
E2: Insured person is car driver
E3: Insured person is truck driver
A : Meets with an accident

Question 8.
A factory has two machines A and B. Past record shows that machine A produced 60% of the items of output and machine B produced 40% of the items. Further, 2% of the items produced by machine A and 1% produced by machine B were defective. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by machine B?
Answer:
E1 : Item produce by machine A
E2: Item produce by machine B
A : Item is defective

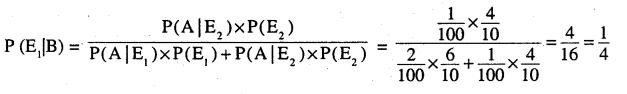
Question 9.
Two groups are competing for the position on the Board of directors of a corporation. The probabilities that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced was by the second group.
Answer:
E1 : 1st group will win
E2 : 2nd group will win
A : New product is introduced
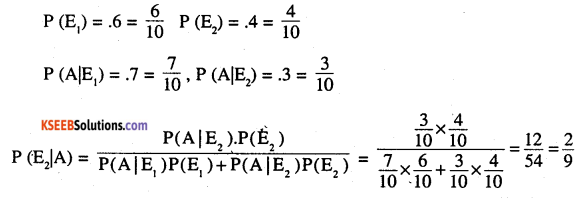
![]()
Question 10.
Suppose a girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4, she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw 1, 2, 3 or 4 with the die?
Answer:
E1 : 5 or 6 shows on the die HHH
E2 : 1, 2, 3,4 shows on the die HHT
A : Shows Head exactly once HTH

Question 11.
A manufacturer has three machine operators A, B and C. The first operator A produces 1% defective items, where as the other two operators B and C produce 5% and 7% defective items respectively. A is on the job for 50% of the time, B is on the job for 30% of the time and C is on the job for 20% of the time. A defective item is produced, what is the probability that it was produced by A?
Answer:
E1 : item produce by A
E2 : item produce by B
E3 : item produce by C
A : item produced is defective

Question 12.
A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are . drawn and are found to be both diamonds. Find the probability of the lost card being a diamond.
Answer:
Let E1 : Lost card is diamond.
E2 : Lost card is not diamond
A : Two cards drawn are diamond

![]()
Question 13.
Probability that A speaks truth is \(\frac{4}{5}\) A coins is tossed. A reports that a head appears. The probability that actually there was head is
(A) \(\frac{4}{5}\)
(B) \(\frac{1}{2}\)
(C )\(\frac{1}{5}\)
(D) \(\frac{2}{5}\)
Answer:
Let E1 : Head appers
E2 : Tail appers
A : Reports that head appears

Question 14.
If A and B are two events such that A⊂B and P(B) ≠ 0,then which of the following is correct?
(A) \(\mathbf{P}(\mathbf{A} | \mathbf{B})=\frac{\mathbf{P}(\mathbf{B})}{\mathbf{P}(\mathbf{A})}\)
(B) P(A|B) < p(A)
(C) P(A|B) ≥ p(A)
(D) None of these
Answer: