Students can Download Maths Chapter 9 Differential Equations Ex 9.3 Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 9 Differential Equations Ex 9.3
2nd PUC Maths Differential Equations NCERT Text Book Questions and Answers Ex 9.3
In each of the Exercises 1 to 5, form a differential equation representing the given family of curves by eliminating arbitrary constant a and b.
Question 1.
\(\frac{x}{a}+\frac{y}{b}=1\)
Answer:
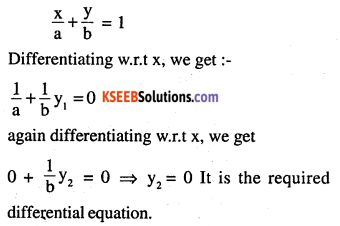
Question 2.
y2 = a (b2 – x2)
Answer:
y2 = a (b2 – x2)
Differentiating w.r.t x, we get
\(2 y \frac{d y}{d x}=a(0-2 x) \Rightarrow 2 y y_{1}=-2 a x\)
=y y, = -ax ………(1)
differentiating again
yy2 + yy1 = -a …(2)
putting value of (-a) from (2) in (1)
yy1= (yy2 + y1y1) x
⇒ y y, = x (y12 + yy2) which is required differential equation.
Note:-
Try to form differential equation with lowest order by removing all arbitrary constants
![]()
Question 3.
y = a e3x + b e-2x
Answer:
y = a e3x + b e_2x ….(1)
Differentiating w.r.t x , y, = ae3x.3 + be 2x (-2) ….(2)
multiply (1) by 3
⇒ 3y = 3ae3x + 3be_2x
⇒ 3ae3x = 3y -3be-2x …(3)
put (3) in (2), we get y, = 3y – 3be-2x – 2 be-2x
⇒ y – 3y = -5 be-2x …….. (4)
differentiating again
⇒ y2 – 3y1 = -5 be-2x (-2) ….(5)
multiply (4) by 2, we get
⇒ 2y,-6y = -10be 2x ….(6)
putting (6) in (5), we get
⇒ -(2y1 – 6y) = y2 -3y1
⇒ y2 – 3y1 + 2 (y1 3y) = 0
⇒ y2 -yt – 6y = 0 is the required differential equation.
Question 4.
y = e2x (a + bx)
Answer:
y = e2x (a + bx) …(1)
differentiating w.r.t x, we get
⇒ y1= e2x (0 + b) + (a + bx) e2x 2
⇒ y1 = e2xxb + (a + bx) e2x 2 ….(2)
putting (1) in (2),
y1 = be2x + 2y ⇒ y1 – 2y = b e2x ….(3)
again differentiating w.r.t x, we get
y2 – 2y1 = b.e2x.2 ….(4)
putting (3) in (4) we get
y2 – 2y1 = 2y1 – 4y
⇒ y2 – 4y1 + 4y = 0 is
the required differential equation.
![]()
Question 5.
y = ex (a cos x + b sin x)
Answer:
y1 = ex (a cos x + b sin x) ….(1)
differentiate w.r.t x
y1 = ex (a cos x + b sin x) + ex (-a sin x + b cos x) ….(2)
putting (1) in (2); we get
⇒ y1 = y + ex (b cos x – a sin x)
⇒ y1 – y = ex (b cos x – a sin x) ….(3)
again differentiating w.r.t x, we get
⇒ y2 – y1 = ex (b cos x – a sin x) +ex (-b sin x – a cos x) ….(5)
putting (3) and (1) in (5), we get
⇒ y2 – y1 = (y1 – y) +(-y)
⇒ y2 – y1 + 2y = 0 is the required differential equation.
Question 6.
Form the differential equation of the family of circles touching the y-axis at origin.
Answer:
Any circle that touches ‘y’ axis at origin should have centre on ‘x’ axis and pass through origin. If centre is (h, 0) then radius is distance between (h, 0) and (0,0), so radius
\(=\sqrt{(h-0)^{2}+(0-0)^{2}}=h\)
Equation of circle
= (x – h)2 + (y – 0)2 = radius2 = h2
⇒ x2 + h2 – 2hx + y2 = h2
⇒ x2-2hx + y2 = 0 …(1)
differentiating w.r.t x, we get
⇒ 2x + 2y y, – 2h = 0 …(2)
multiply (2) with x and subtracting from (1), we get
⇒2x2 + 2y y1 x – 2hx – x2 + 2hx – y2 = 0
⇒ x2 – y2 + 2y y1 x = 0 is the required differential equation.
Question 7.
Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Answer:
Equation of parabola required in question is:-
x2 = 4 ay ………… (1)
a is parameter differentiating w.r.t x, we get
2x = 4ay ……….. (2)
putting (1) in (2), we get x2
\(2x=\frac{x^{2}}{y} y_{1} \Rightarrow 2y=x y_{1} \Rightarrow x y_{1}-2 y=0\)
required differential equation.
![]()
Question 8.
Form the differential equation of the family of ellipses having foci on y-axis and centre at origin.
Answer:
Equation of ellipse required in question is
\(\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1\)
a=semi major axes (along ‘y’axis)
b = semi minor axes differentiating w.r.t x, we get

Question 9.
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.
Answer:
Equation of hyperbola required in question is:-

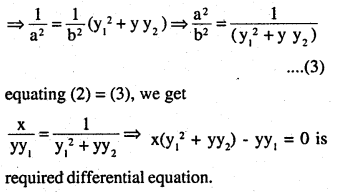
Question 10.
Form the differential equation of the family of circles having centre on y-axis and radius 3 units.
Answer:
Required equation of circle is :-
(x – 0)2 + (y – k)2 = 32 ……….(1)
(k is any value) – as along ‘y’ axis, centre will be (0, k)
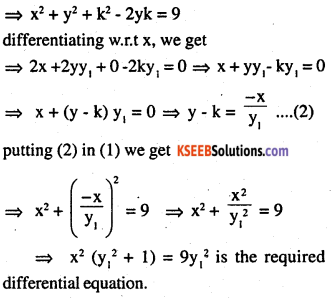
![]()
Question 11.
Which of the following differential equations has y = c1 ex + c2 e-x as the general solution?
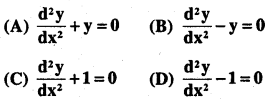
Answer:

but (1) = (3)
⇒ y = y2
so y2 – y = 0
so correct answer is (B).
Question 12.
Which of the following differential equations has y = x as one of its particular solution ?
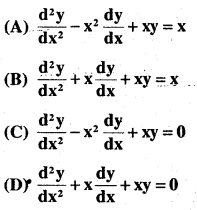
Answer:
y = x
y1 = 1 y2 = o
this is satisfied by
y2 – x2 y, + xy = 0
0 – x2 x 1 + x x x = 0
so answer is (C).