You can Download Chapter 10 Wave Optics Questions and Answers, Notes, 2nd PUC Physics Question Bank with Answers, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Physics Question Bank Chapter 10 Wave Optics
2nd PUC Physics Wave Optics NCERT Text Book Questions and Answers
Question 1.
Monochromatic light of wavelength 589 nm is incident from air on a water surface. What are the wavelength, frequency and speed of
(a) reflected, and
(b) refracted light? Refractive index of water is 1.33.
Answer:
\({ ^{ a }{ \mu } }_{ W }\)=1.33
\({ { \lambda } }_{ air }=589nm=589\times { 10 }^{ -9 }\)
(a) For reflected light:- On reflection, no change occurs in wavelength, frequency and speed of the incident light.
Velocity of the reflected light = 3 x 108 ms-1
wavelength of the reflected light = 589 nm

The frequency is a inherent characteristic of radiation. It does not change on refraction.
∴ Frequency of the refracted light = 5.09 x 1014Hz.
![]()
Question 2.
What is the shape of the wave front in each of the following cases:
(a) Light diverging from a point source.
(b) Light emerging out of a convex lens when a point source is placed at its focus.
(c) The portion of the wave front of light from a distant star intercepted by the Earth.
Answer:
(a) Spherical shape
(b) Plane wave front
(c) Plane wave front
Question 3.
(a) The refractive index of glass is 1.5. What is the speed of light in glass? (Speed of light in vacuum is 3.0 x 108 ms-1)
(b) Is the speed of light in glass independent of the colour of light? If not, which of the two colours red and violet travels slower in a glass prism?
Answer:
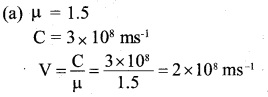
(b) The speed of light in glass is not independent of the colour (wavelength) of light of the two, violet light travels slower in a glass prism.
Question 4.
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
Answer:

Question 5.
In Young’s double-slit experiment using monochromatic light of wavelength A, the intensity of light at a point on the screen where path difference is x, is K What is the intensity of light at a point where path difference is λ /3?
Answer:
When the path difference is λ :
When two light waves of amplitudes a, and a2 superpose each other at a point, then the intensity of light at that point is given by,
I = a2 + a2 +a1a2 cosφ ………………..(1)
where φ is the phase difference between the two waves.
a1 = a2 = a (say), I = K units.
Also, the path difference of λ is equivalent to a phase difference of 2π i e.
φ = 2 π rad= 360°
equation (1) becomes,
K = a2 + a2 + 2a x a cos 360°
= 2a2 + 2a2 x 0
a2 = k/2 …………………………. (2)

Question 6.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
(a) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
(b) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
Answer:
λ = 650nm = 650 x 10-9m
λ1 =520nm = 520 x 10-9m
(a) A distance of nth bright fringe from the central maximum,
\({ y }_{ n }=\frac { nDx }{ d } \)
∴ Distance of the third bright fringe (n = 3) for wavelength λ(-650 x 10-9 m),

(b) Suppose that the nth bright fringe due to wavelength X coincides with the nth bright fringe due to wavelength λ1

![]()
Question 7.
In a double-slit experiment, the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
Answer:
λ= 600 nm = 600 x 10-9 m D= lm
The angular width of the fridge,
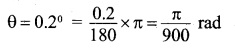

Question 8.
What is the Brewster angle for air to glass transition? (Refractive index of glass = 1.5.) Answer:
µ = 1.5
According to Brewster’s law,
µ = tan p
tan p = 1.5
= p=56.31º
Question 9.
Light of wavelength 5000 A falls on a plane reflecting surface. What are the wavelength and frequency of the reflected light? For what angle of incidence is the reflected ray normal to the incident ray?
Answer:
X = 5000A = 5 x 10-7 m
on reflection, no change occurs in wavelength, frequency and speed of the incident light.
∴ Wavelength of reflected light = 5000Å.
Taking C = 3 x 108 ms-1. The frequency of reflected light is given by
\(V=\frac { C }{ \lambda } =\frac { 3\times { 10 }^{ 8 } }{ 5\times { 10 }^{ 7 } } =6\times { 10 }^{ 14 }Hz\)
The reflected ray is normal to the incident ray, when the angle of incidence is equal to 45°
Question 10.
Estimate the distance for which ray optics is good approximation for an aperture of 4 mm and wavelength 400 nm.
Ans:
a = 4mm = 4x 103m
λ = 400nm = 400 x 10-9 m
\({ Z }_{ r }=\frac { { a }^{ 2 } }{ \lambda } =\frac { (3\times { 10 }^{ -3 })^{ 2 } }{ 400\times { 10 }^{ -9 } } =40m\)
2nd PUC Physics Wave Optics Additional Exercises
Question 11.
The 6563 Å H α line emitted by hydrogen in a star is found to be redshifted by 15 Estimate the speed with which the star is receding from the Earth.
Answer:
x = 6563 A = 6563 x 10-10 m
ΔX = 15 A = 15 ×10-10 m
Let V be the speed with which the star is receding from the earth. Then, from Doppler’s effect in light,

The negative sign shows that the star is receding.
![]()
Question 12.
Explain how Corpuscular theory predicts the speed of light in a medium, say, water, to be greater than the speed of light in vacuum. Is the prediction confirmed by experimental determination of the speed of light in water? If not, which alternative picture of light is consistent with the experiment?
Answer:
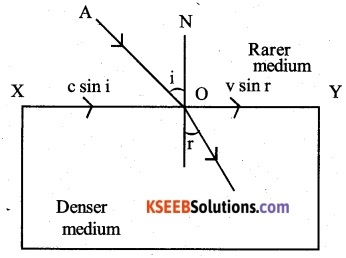
Suppose that the light corpuscles traveling with a velocity C in rarer medium along A O strike the interface X Y separating the denser medium (say, water) from a rarer medium as shown in above figure. After refraction, the light corpuscles travel inside he denser medium along O B with a velocity V. Let i and r be the angles of incidence and reflection respectively.
According to Newton’s corpuscular theory, the light corpuscles experience a force of attraction due to the denser medium, which acts along normal to the interface X Y. Obviously, the component of their velocities before and after the refraction along X Y must remain the same.

medium is greater than that in a rarer medium. This result of the corpuscular theory is against the experimental result and therefore this theory was discarded. On the basis of Huygen’s wave theory, the phenomenon of refraction can be easily explained and it can be proved that c >v. Therefore, wave picture of light is consistent with experimental result.
Question 13.
You have learnt in the text how Huygens’ principle leads to the laws of reflection and refraction. Use the same principle to deduce directly that a point object placed in front of a plane mirror produces a virtual image whose distance from the mirror is equal to the object distance from the mirror.
Answer:
Consider that a point object O is placed in front of a plane mirror x y and a spherical wavefront APB originating from the object is incident on the mirror as shown in figure
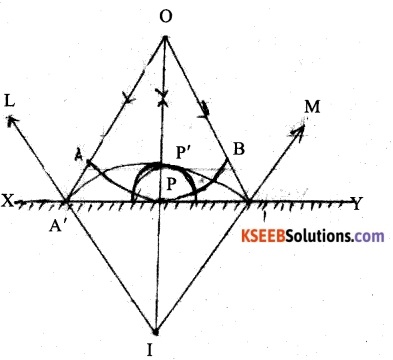
The lines OA, OP and OB (normal to the incident wavefront APB at the points a’ P
and B) represent the incident rays. Since the distance OP is smaller than O a’ or OB’ > the disturbance will reach the point P earlier than it reaches the points a’ and b’ on the mirror.
Therefore, the instant, when the disturbance reaches the points a’ and b’ > the secondary wavelet from the point P will grow into a sphere of radius ((OA’ – OP) or (OB’ – OP). At this instant, the points a’ and b’ on the mirror have just become the sources of secondary wavelets and therefore, the secondary wavelets originating from these points will be ‘of zero radius at that instant.
To find the reflected wave front (new position of the wave front after reflection from the plane mirror); with the point P as centre, draw a sphere of radius PP’ = (OA’-OP) or (OB’-OP). Then, the sphere A’ P’ B’, the common envelope of the secondary wavelets issuing out from the points a’, p’ and b’ gives the reflected wave front (diverging) and the lines IAS IP’ and jb’ normals to the reflected wave front represent the reflected rays. The point I, from which the reflected wave front appears to come from, is the virtual image of the object O From simple geometry,
IP = OP
i..e, image is formed as for behind the plane mirror as the object is in front of it.
Question 14.
Let us list some of the factors, which could possibly influence the speed of wave propagation:
(i) Nature of the source.
(ii) Direction of propagation.
(iii) Motion of the source and/or observer.
(iv) Wavelength
(iv) Intensity of the wave.
On which of these factors, if any, does
(a) The speed of light in vacuum,
(b) The speed of light in a medium (say, glass or water), depend?
Answer:
(a) Dependence of the speed of light in a vacuum: The speed of light in vacuum is a universal constant. It is independent of all the factors listed above. It may be pointed out that Newton ion relativity principle does not apply to the speed of light. The fact that the speed of light is independent of the relative motion between the source and the observer is one of the postulates of Einstein’s special theory of relativity.
(b) Dependence of the speed of light in a medium:
- It does not depend on the direction of propagation, provided the medium is isotropic.
- It does not depend on the relative motion between the source and the medium. However, it depends on relative emotion between, the source and the observer
- It depends on the wavelength
- It does not depend on the intensity.
![]()
Question 15.
For sound waves, the Doppler formula for frequency shift differs slightly between the two situations:
(i) source at rest; observer moving, and
(ii) source moving; observer at rest. The exact Doppler formulas for the case of light waves in vacuum are, however, strictly identical for these situations. Explain why this should be so. Would you expect the formulas to be strictly identical for the two situations in case of light travelling in a medium?
Answer:
Doppler effect for sound waves is asymmetric i.e. for the same relative motion in the cases (i) and (ii), the apparent change in the frequency is not the same. It is because, sound waves require a medium for their propagation and the motion of the observer relative to the medium is different in two cases.
Doppler effect for light waves is symmetric i.e. for the same relative motion in the case
(i) and (ii), the apparent change in the frequency is same. For light waves in vacuum, there is no difference in the two cases. It is because, the relative motion between the source and the observer is not affected, whether the source is in motion or the observer is in motion. However, for the light waves in medium, the situations in the two cases are different as in the case of Doppler effect for sound waves. Likewise the formulas for Doppler effect in the two cases will be different.
Question 16.
In double-slit experiment using light of wavelength 600 nm, the angular width of a fringe formed on a distant screen is 0.1°. What is the spacing between the two slits?
Answer:

Question 17.
Answer the following questions:
(a) In a single slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band?
(b) In what way is diffraction from each slit related to the interference pattern in a double-slit experiment?
(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why?
(d) Two students are separated by a 7 m partition wall in a room 10 m high. If both light and sound waves can bend around obstacles, how is it that the students are unable to see each other even though they can converse easily.
(e) Ray optics is based on the assumption that light travels in a straight line. Diffraction effects (observed when light propagates through small apertures/slits or around small obstacles) disprove this assumption. Yet the ray optics assumption is so commonly used in understanding location and several other properties of images in optical instruments. What is the justification?
Answer:
(a) The width of central maximum
\(\frac { 2D\lambda }{ a } \)
If the width of the slit
(a) is made double of the original, the width of the central diffraction band will reduce to half. The intensity of the central diffraction band coil become four times.
(b) The intensity of interference fringes in young’s double slit experiment is superposed by the diffraction pattern of each slit.
(c) The central bright spot is produced due to the constructive interferences of the waves from the edge of the circular obstacle.
(d) For pronounced diffraction effect, the size of the obstacle should be comparable to the wavelength of the waves. The size of partition is very large as compared to the wavelength of light and hence it is not diffracted and the two students cannot see each other.
(e) In optical instruments, the sizes of the aperture is very large as compared to the wavelength of the light used. As such, the diffraction of light wave is of no significance.
![]()
Question 18.
Two towers on top of two hills are 40 km apart. The line joining them passes 50 m above a hill halfway between the towers. What is the longest wavelength of radio waves, which can be sent between the towers without appreciable diffraction effects?
Answer:
The hills will not obstruct the transmitted radio waves, if over the halfway distance (Zf) between the hills, the spreading of the signal is limited to the distance (a) of the line of sight from the hills.

Question 19.
A parallel beam of light of wavelength 500 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1 m away. It is observed that the first minimum is at a distance of 2.5 mm from the centre of the screen. Find the width of the slit.
Answer:
λ= 500nm = 500 x 10-9m
D = 1m
The distance of first minimum from the centre of the screen,

Question 20.
Answer the following questions:
(a) When a low flying aircraft passes
overhead, we sometimes notice a slight shaking of the picture on our TV screen. Suggest a possible explanation.
(b) As you have learnt in the text, the principle of linear superposition of wave displacement is basic to understanding intensity distributions in diffraction and interference patterns. What is the justification of this principle?
Answer:
(a) A low flying aircraft reflects the TV signal. Due to interference between the direct signal and the reflected signal, the picture on TV screen shows a slight shaking.
(b) A wave equation can be expressed as a differential equation. The super position principle follows from the linear character of the wave equation. If y1 and y2 are the solutions of the wave equation, then their any linear combination is also the solution of the wave equation.
Question 21.
In deriving the single slit diffraction pattern, it was stated that the intensity is zero at angles of n%/a. Justify this by suitably dividing the slit to bring out the cancellation.
Answer:
Divide the slit of width an into n parts, so that the width of each small part of the slit is
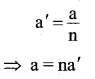
For a path difference nλ between the waves from two extreme ends of the slit,
\(\theta =\frac { n\lambda }{ a } =\frac { n\lambda }{ n{ a }^{ \prime } } =\frac { \lambda }{ { a }^{ \prime } } \)
Each of the n parts of the slit will send zero intensity in the direction 0. Obviously, all the n parts together will also give zero intensity.
2nd PUC Physics Wave Optics Additional Questions and Answers
Question 1.
Two coherent sources, whose intensity ratio is 10: 1 produce interference fringes. Calculate the ratio of intensity of maxima and minima in the fringe system.
Answer:

Question 2.
In young’s double slit experiment, the two slits are 0.5 mm apart. The screen is placed lm away from the slits. The distance of 11th fringe from the first fringe is 1 cm. Calculate the wavelength of light used.
Answer:
The distance of the 11th fringe from the first fringe is equal to width of 10 fringes.

Question 3.
Determine the angular separation between central maximum and first order maximum of the diffraction pattern due to a single slit of width 0.25mm, when light of wavelength 5890 Å is incident on it normally.
Answer:

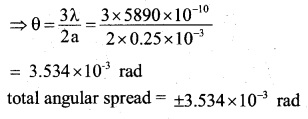
![]()
Question 4.
Two spectral lines of sodium D1 and D2 have wavelengths of approximately 5,890 and 5896 Å sodium lamp sends incident plane wave on a slit of width 2 x 106 m. A screen is located 2m from the slit. Find the spacing between the first maxima of two sodium lines as measured on the screen.
Answer:
The distance of first secondary maxima from the centre of screen,

Question 5.
Colours appear on a thin soap film and soap bubbles due to the phenomenon of
(A) interference
(B) scattering
(C) diffraction
(D) dispersion
Answer:
(A) interference
Question 6.
The frequency of an e.m. wave which is best suited to observe a particle of radius
3 x 10-6 m, is of order of
(A) 1015
(B) 1013
(C) 1014
(D) 1012
Answer:
The particle can be observed when wavelength of light used is of the order of its size. Therefore, required frequency
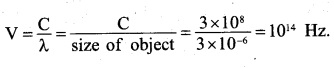
Question 7.
Golden view of sea shell is due to
(A) diffraction
(B) dispersion
(C) polarisation
(D) reflection
Answer:
(C) polarisation
Question 8.
In a young’s experiment, two coherent sources are placed 0.9mm apart and the fringes are observed lm away. If it produces the second dark fringe at a distance of 1mm from the central fringe, the wavelength of monochromatic light used would be
(A) 60 x 10-4cm
(B) 10 x 10-4 cm
(C)10 x 10-5cm
(D) 6 x 10-5cm
Answer:

Question 9.
For the relaxed eye, the magnifying power of microscope is.
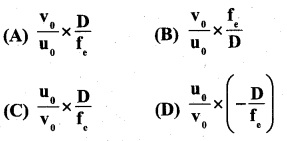
Answer:
(A)
![]()
Question 10.
In a Fresnel biprism experiment, the two positions of lens give separation between the slits as 16cm and 9cm respectively. What is the actual distance of separation?
(A) 12.5cm
(B) 12cm
(C) 13cm
(D) 14cm
Answer: (B)
The actual distance of separation between the slits,
\(d=\sqrt { { d }_{ 1 }{ d }_{ 2 } } =\sqrt { 16\times 9 } =12cm\)