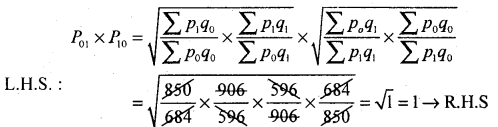You can Download Chapter 2 Index Numbers Questions and Answers, Notes, 2nd PUC Statistics Question Bank with Answers Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Statistics Question Bank Chapter 2 Index Numbers
2nd PUC Statistics Index Numbers One and Two Marks Questions and Answers
Question 1.
What do you mean by an index number?/ Define index numbers.
Answer:
An index number is a statistical measure designed to show an average change in a variable or group.of related variables with respect to Time, Geographical location or Income group etc.
Question 2.
Define/what are the conditions for an Index number to satisfy TRT and FRT.
Answer:
Time Reversal Test requires that the product of P01 (price index number computed time backward) and P10 (price index number computed time forward) should be equal to one [1]; ie P01 × p10 = 1.
Factor Reversal Test requires that the product of P01 (price index number) and Q01 (quantity index number) should be equal to the net changes occurring in between the current year and the base year (V01 )
ie. P01 × Q01 = \(\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{0}}\);(Except the factor 100)
Question 3.
Define Unit Test
Answer:
This test requires that the index number used should be independent of the units of measurement.
Question 4.
Define Circular test
Answer:
This requires that the index number is to work in a circular manner and this property enables us to find the index numbers from period to period without referring back to the original base each time. For 3 years 0(1998), 1(2005) and 2(2010):
Circular test is said to be satisfied if: P01 × P12 × P20 = 1
![]()
Question 5.
What is a price relative?
Answer:
Price Relative is the price in the current year expressed as percentage of the price in the base
P = \(\frac{p_{1}}{p_{0}}\) × 100
Question 6.
Write the formula for unweighted geometric mean index number .
Answer:
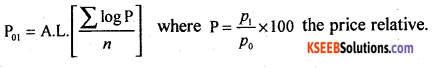
Question 7.
The sum of the price relaives of 5 different is 220. Find suitable Unweighted price index number
Answer:
Here Unweighted price Index number: P01 = = 40
Question 8.
If cost of living Index number of 2005 is 225 with 1995 as a base year, what is the change in the Index?
Answer:
The percentage change in consumer prices is 125%
Question 9.
Define consumer price/cost of living index number.
Answer:
“Cost of living index number is the index number of the cost met by a Specified class of consumers in buying a basket of goods and services.”
Question 10.
Why Index numbers are called ‘Economic Barometers’?
Answer:
A Barometer measures the pressure of the atmosphere. An index number indicates the changes occurring in Economic field such as variations in price, costs, growth rate, imports, exports of certain commodities etc.
Question 11.
Theoretically which best average is used in the construction of Index Number?
Answer:
Geometric mean
Question 12.
Price index number for the current is 200, give your conclusion.
Answer:
There is a net increase of prices by 100% in the current year as compared to base year
Question 13.
Mention any two steps in the construction of Index Number.
Answer:
Any two of the following :
- Purpose and the scope
- Selection of base period or
- Selection of commodities or items
- Obtaining price quotations
- Choice of an average
- 6. Selection of weights
- Selection of suitable formula
![]()
Question 14.
Name the 2 methods of computing Consumer price Index (cost of living Index) Number?
Answer:
Aggregative expenditure method(AEM) & Family Budget method (FBM).
Question 15.
What do you mean by ‘Family Budget Survey’ conducted while constructing consumer price index number?
Answer:
A detailed enquiry/survey regarding the consumption pattern and the average expenditure spent on various item under the heads-Food, Cloth, Rent, Fuel & Lighting, Education, Entertainment, & Miscellaneous, required for day to day living of the consumers is conducted.
Question 16.
Why Fisher’s Index number is called an Ideal Index Number?
Answer:
Fisher’s Index Number is called as ideal because, it is free from bias in use of weights ie. it takes both current and base year quantities as weights.
- It is based on geometric mean which is considered as best average
- It satisfies both time reversal tests and factor reversal tests
Question 17.
Write the uses of Index numbers.
Answer:
Index numbers are useful to governments in formulating Economic policies, such as Taxation, imports, exports, granting of licenses to new firms, fixation of Bank rates, salary and grants to employees. Also, in comparing variations in production, prices, shares, Demand, supply, and measurement of real Rupee.
Question 18.
The average price level of a commodity in the year 2000 is times of what it was in 1990. Express the change by means of Index number.
Answer:
The average price in 1990 is 100, so the Index number should be 100 × 2 1/2 = 250 in 2000
Question 19.
Which prices of the commodities is useful (used) in the construction of cost of living Index Number?
Answer:
Retail prices of the commodities is used in the construction of consumer price Index Number.
![]()
Question 20.
If the price index for the current year is 125 what is your conclusion?
Answer:
The prices have increased by 25% .
Question 21.
The price index for the current year is 121. Give your conclusion.
Answer:
The prices have increased by 21%
Question 22.
What weights are used in Laspeyre’s, Paasche’s, Marshall-Edgeworth’s Price Index Numbers?
Answer:
Base year, Current year & Arithmetic mean of Base year and Current year Quantities are used as weights.
Question 23.
which average is preferred in the construction of an index number? why
Answer:
A.M or GM. Is used because AM us very easy to calculate where as geometric mean is considered as most appropriate and better method for averaging the ratios.
Question 24.
Which weights are used in Paasche’s Quantity Index No.?
Answer:
Base year prices (P0).
![]()
Question 25.
What is the Index number during the base year?
Answer:
100
Question 26.
If P01(L) for the year 2006 with base year 2000 is 225, what is the Index Number for 2000?
Answer:
100 .
Question 27.
Which test is satisfied by Marshall-Edgeworths’s Index number?/Does Marshall- Edgeworths’s Index number satisfies time reversal test?
Answer:
Time Reversal Test/Yes.
![]()
Question 28.
Give any two Limitations of Price Index Number.
Answer:
- Many formulae are used and they give different answers for the index.
- As the customs and habits change from time to time, the uses of commodities also vary.
- There is ample scope for bias in the construction of Index numbers.
Question 29.
What are the points to remember while selecting the Base Year?AVrite two norms for selecting the base year in the construction Index number
Answer:
Base year selected
- should be the Normal one
- should not be too long or too short period .
- is a fixed or chain base year method
Question 30.
Show that Laspeyre’s price index number does not satisfy time reversal test.
Answer:
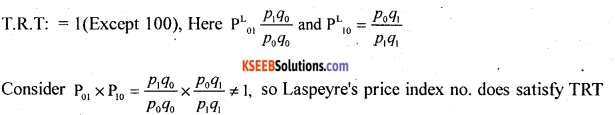
Question 31.
If a price of a commodity is Rs.10 in 2002 aiid Rs.35 in 2008, then compute the index no. of price.
Answer:
Price Index No.[price relativel = \(\frac{P_{1}}{P_{0}}\) × 100 = \(\frac{35}{10}\) × 100 = 350
Question 32.
If Laspeyre’s price index number and paasche’s price index numbers are 210 and 208, then find Dorbish-Bowle’s price index no.
Answer:
The relation between Laspeyre’s ,Paasche’s and Dorbish-bowley price index number is :
D – B = \(\frac{L+P}{2}\) × 100; D-B = \(\frac{210 + 208}{2}\) = 209
Question 33.
Given Σ p1q0 = 100 and Σ p0q0 = 102 find a suitable index no.
Answer:
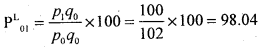
![]()
Question 34.
If Σ p1q1 and Σ p0q1 = 120 find a suitable index number.
Answer:
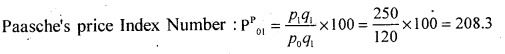
Question 35.
If PL01 for the year 2006 with base year 2000 is 225, what is the index number for 2000?
Answer:
The index number for the year 2000 is ‘100’
Question 36.
If PL01, = 135 and Pp01= 138, find P01 [F].
Answer:
![]()
Question 37.
If Laspeyre’s and Fisher’s indices are 110 and 110.5 respectiely, find Paasche’s index number.
Answer:
P01 [F] = \(\sqrt{\mathrm{P}_{01}(\mathrm{L}) \times \mathrm{P}_{01}(\mathrm{P})}\) ; 110.5 = \(\sqrt{110 \times \mathrm{P}_{01}(\mathrm{P})} \)
(110.52 = 110 × P01(P); P01(P) = 12210.25/110 = 111.0023
![]()
Question 38.
If Σ p0q1 = 250 and Σ p1q1 = 400, compute suitable price index no.
Answer:
Paasche’s price index number p01 = \(\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{1}}=\frac{400}{250}\) = 160
Question 39.
Σ q1p0 = 180 and Σ q0p0 = 150 then find suitable quantity index number.
Answer:
Q01 = \(\frac{\sum q_{1} p_{0}}{\sum q_{0} p_{0}}=\frac{180}{150}\) = 120
Question 40.
Calculate cost of living index number from the following data.

Answer:
I01 = \(\frac{\Sigma p w}{\Sigma w}\) = (110 × 3 + 120 × 8 + 112 × 4 + 108 × 6 + 105 × 9)/(3 + 8 + 4 + 6 + 9) = 104.466
Question 41.
Calculate ‘P01‘ by simple average of price relative method, using Arithmetic Mean

Answer:
P = \(\frac{\mathrm{P}_{1}}{\mathrm{P}_{2}}\) × 100 = [l 12.5,94.44,100,120]; Σ P = 426.94;
∴ P01 = \(\frac{\Sigma P}{n}\) = 106.73
Question 42.
Find V01, given Σ p0q0 = 382 and Σ p1q1 = 424
Answer:
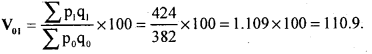
Question 43.
Construct consumer price Index number from the following data.
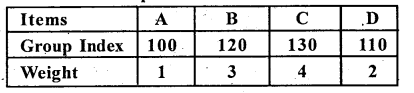
Answer:
I01 = \(\frac{\Sigma p w}{\Sigma w}\) = [100 × 1 + 120 X 3 + 130 × 4 + 110 × 2]/[1 + 3 + 4 + 2] = 1200/10 = 120
Question 44.
How Laspeyre’s , Paasche’s and Dorbish Index numbers are related?.
Answer:
Arithmetic mean of Laspeyr’s and Paasche’s Index numbers
D – B = \(\frac{\mathrm{L}+\mathrm{P}}{2}\)
Question 45.
Who are specific consumers considered in the construction of Index Number?
Answer:
Here the specific class consumers means group of consumers who are having similar pattern of consumption. Generally those of factory workers, government employees, and the consumers who belonging to a particular community etc.
![]()
Question 46.
What is meant by simple index number?
Answer:
The index number being constructed for a single item is a simple or Univar rate index number.
Question 47.
What is meant by composite index number?
Answer:
The index number being constructed for group of items is a composite index number.
Question 48.
Mention the characteristics of index number.
Answer:
Index numbers:
- Are specialised averages.
- Are expressed in ratios but expressed in percentages.
- Study the effect of factors which cannot be measured directly.
- Facilitates comparision.
Question 49.
What is meant by fixed base and chain base in index number?
Answer:
If the period of comparision is fixed for any current year, is called as fixed base year.
If the. period of comparision is immediate preceeding period for any current year, is called chain base year.
Question 50.
What are quantity weights and value weights?
Answer:
A quantity weight is the amount of commodity used or produced during a period.
A value weight is the product of price and quantity used during a period.
Question 51.
Define base year and current year in index number.
Answer:
The year selected for comparision is the base year and the year for which comparisons are required is the current year.
Question 52.
If the general price level goes up by 80% between 2002 and 2012, What is the index number for 2012 with base 2000?
Answer:
Index number for the year 2012 = 180. .
Question 53.
which averages are commonly used in the construction of index number?
Answer:
Simple Arithmetic Means (x̄), weighted. An (x̄w) an
Question 54.
If total value in base year and current year are respectively 800, and 1000, compute value Index number.
Answer:
Value I.NO. V01 = \(\frac{\Sigma p_{1} q_{1}}{\Sigma p_{0} q_{0}}\) × 100
\(\frac{1000}{800}\) × 1000 = 125
Question 55.
What is the relation between Laspeyre’s, Paasche’s and Fishers Index numbers?
Answer:
\(\sqrt{L \times p}\)
![]()
Question 56.
Give the meaning of Base year.
Answer:
The year against which comparisions are made is called base year
Question 57.
What is normal Base year?
Answer:
Normal Base year is the year in which in that year there are no accidents / natural calamities occurred, which affect the business and economic activities.
(OR)
Normal base year is the year in which in that year there are no wars, floods, famine, tsunami, strikes etc.
Question 58.
Define price Index numbers.
Answer:
Price Index numbers indicates the general level of prices of articles over a period of time
Question 59.
Define value Index number.
Answer:
Value Index number indicate the effect of combination of price and quantity changes in between the two periods.
Question 60.
What test is satisfied by Marshall-Edge worth’s Index number?
Answer:
Timer reversal test..
Question 61.
If Index number in 2005 is 225 with base as 1995, what is the change in the Index?
Answer:
The percentage change is 125%.
Question 62.
The average price level of a commodity in the year 2000 is 2\(\frac{1}{2}\) times of what it was in 1990. Express the change by means of Index number.
Answer:
The average price in 1990 is 100, so, the Index number in 2000 should be 100 × 2\(\frac{1}{2}\) = 250.
Question 63.
Give the formula for constructing weighted geometric niean price index number.
Answer:
P01 = Antilog{ \(\frac{\sum w \log p}{\sum w}\) } ,Where w is weight and \(\frac{P_{1}}{P_{0}}\) × 100
Question 64.
Write the expression for Marshall-Edgeworth’s Quantity Index Number.
Answer:
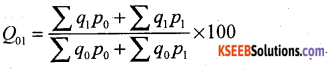
Question 65.
Given Σ p1q0 =100 and Σ p0q0 =102 find a suitable index number.
Answer:
Laspeyre’s Price Index Number
P01 = \(\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}}\) × 100 = \(\frac{100}{102}\) × 100 = 98.04 01
![]()
Question 66.
Distinguish between weighted and unweighted / simple index numbers
Answer:
In weighted index numbers due weightage is given to different items in a relative way i.e., equal importance is not given to all items, where as in unweighted index numbers weights used are all uniform.
Question 67.
From the following data, calculate simple aggregative index number.

Answer:
Simple Aggregative Index number p01 – \(\frac{\sum P_{1}}{\sum P_{0}}\) × 1000
Here P0 – Price in in 1990
P1– Price in 2000
Σ p0 = 70, Σ p1 = 76, p01= \(\frac{76}{70}\) × 100 = 108.57.
![]()
Question 68.
Calculate simple aggregate price index number for the following data.

Answer:
Simple aggregative price index number,

Question 69.
Show that Marshall – Edgeworth’s Index number satisfies Time reversal lest.
Answer:
Marshall-Edgeworth’s Price Index number,

Question 70.
What are Simple and Weighted Index numbers ?
Answer:
In Simple (unweighted) price Index numbers, an average of price relatives are calculated using Arithmetic mean and Geometric mean.
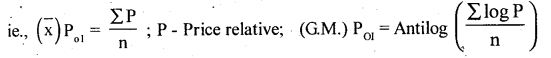
In Weighted price Index numbers appropriate weights are assigned to various items, and weighted average of price relatives are calculated using Arithmetic mean ad Geometric mean.
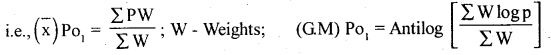
And Similarly, Simple and Weighted aggregative Index numbers are computed.
Question 71.
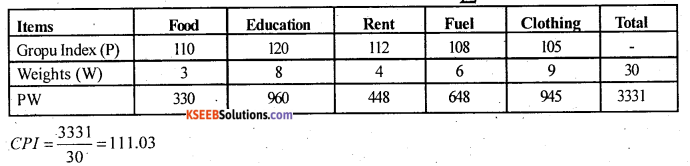
Calculate cost of living index number from the following data.

Answer:
Here, Group index = price relatives = P \(\frac{\mathrm{p}_{1}}{p_{0}} \times 100\) and weights – w are given so use Family
Budget Method: Consumer price index number (CPI); CPI = \(\frac{\sum p w}{\sum w}\)
2nd PUC Statistics Index Numbers Five Marks Questions and Answers
Question 1.
Mention the steps involved in the construction of Price Index Number? Explain in brief. (10 Marks)
Answer:
Following are the steps/stages/principles/Fleads. involved:-
- Purpose and the scope
- Selection of base period
- Selection of commodities or items
- Obtaining price quotations
- Choice of an average
- Selection of weights
- Selection of suitable formula
1. Purpose and scope:-
At the very outset the purpose for which the index numbers is being constructed should be clearly defined. Since most of the latter problems will depend upon purpose, because the selection of items, base year, formulae will be different for different purposes. The purpose may be such as cost of living index number for urban areas, rural areas, factory workers etc. should be clearly defined.
Also, it is necessary to state the scope of the index numbers such as, geographical region, time, Income etc.
2. Selection of the Base year: –
Index numbers are always constructed with reference to some period called base period. The period may be a year, a month, week or a day.
Following points are to be considered while selecting the base year.
- The base period selected should be Normal one, that is economically stable. It should be free from wars, floods, famine, booms, depressions, which affects the economic activities.
- Also the base year selected should not be too long or too short distance. Since economic activities are always dynamic.
- While selecting the base year, decision has to make whether fixed base or chain base year to be selected. In fixed base year, if the period of comparison is kept fixed for all current years, it is called fixed-base period. Where as in chain base year, comparison is made always with the previous year.
3. Selection of items: –
Items means sample of representative commodities/ items, required for day to day living, which are included in the construction of index number. According to the tastes, habits, customs and traditions etc., of working class people should be selected. It is also necessary to decide the grade or quality of items.
4. Obtaining price quotations: –
After selecting the commodities/ items, the next problem is to fix the prices for the items selected. Since prices vary from place to place, and even from shop to shop in the same market. Hence the suitable way is to obtain the prices ascertained by Marketing inspectors, Super Bazaars, Co-operative Societies or took out the average prices collected by various shops or places where concerned.
5. Choice of an average:-
Since index numbers are specialised averages so, in the construction of index numbers, suitable average should be used. The choice is made between Arithmetic mean and Geometric mean. Usually Arithmetic mean with weighted averages is popularly applied, but when accuracy is required Geometric mean is suitable.
6. Selection of Weights:-
Weight of the items means, the relative importance of an items used in the construction of index number. Since all items are not equally important in day-to-day usage. Proper weights should be attached to the various items depending on their relative importance, eg: Sugar-Rice, Atta-Salt etc. Mostly these weights are quantities in the base period or . those in the current period are considered. Sometimes a combination of quantities of different time periods may be used as weights.
7. Selection of formula:-
A large number of formulae have been devised for construction of Index numbers. Hence a reasonable formula/ method suitable to the object and the data available should be selected.
![]()
Question 2.
What are the steps used in the construction of Consumer Price Index Number? Explain in brief. .
Answer:
Here “Cost of living index number is the index number of the cost met by a specified class of consumers in buying a basket of goods and services.
The following are the main steps/stages/principlps/points/Heads involved in the construction of cost of living index numbers: –
- Object and scope.
- Conducting family budget survey
- Obtaining the price quotation.
- Method of construction.
1. Object and Scope:-
Decide the class of consumers for which index number is required. Such as whether index number is meant for government employees, bank employees, merchants, farmers, etc. also the geographical location, as that of locality, city or town, or a community of people who are having the similar consumption pattern should be decided.
2. Conducting family budget survey:-
A sample survey regarding the average expenses of families on various items of consumption is conducted. In the survey, the information regarding commodities consumed by the families, their quality and the respective budget is collected. The items included are under the heads of (i) Food (ii) Clothing (iii) Fuel and lighting and (iv) Miscellaneous. Each of these can be divided into smaller groups, as food may be including Wheat, Rice, Dhal, etc., which are consumed by the people for whom index is meant.
3. Obtaining Price Quotations:
While constructing the cost of living index number, retail prices of commodities/ items are to be collected. The price lists are obtained from different agencies from different places. Then, they are averaged and these averages are used in the construction of index number. Here price lists of current period as well as base period should be collected.
4. Methods of construction:¬. There are two methods of construction of Consumer price Index Number
- Aggregative Expenditure Method (AEM): In this method base year quantities are considered as weight, i.e. C.P.I = \(\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}}\) × 100
- Family Budget Method (FBM): In this method weighted AM of price relatives are used i.e CPI = \(\frac{\sum p w}{\sum w}\) ;Where P = \(\frac{p_{1}}{p_{0}}\) x 100; W = weight (p0q0)
Question 3.
Explain Time Reversal Test and Factor Reversal Tests,
Answer:
Time Reversal Test: (TRT) :
This test requires that the index number computed backwards should be the reciprocal of the index number computed forward, except the factor 100.
i.e. P01 = \(\frac{1}{\mathrm{P}_{10}} \) OR P01 × P10 = 1 (Except the factor 100)
Factor Reversal Test:- This test requires that the product of the Price Index number and the Quantity Index number should be equal to the net change in the value taking place between two periods, except the factor 100.
i.e. P01 × Q01 = \(\frac{\sum p_{1} q_{1}}{\sum p_{0} q_{0}}\) = V01(Except the factor 100)
Question 4.
From the following data calculate (i) unweighted Arithmetic mean index number (ii) unweighted geometric mean index number.

Answer:
Unweighted Arithmetic mean index number : P01 = \(\frac{\sum P}{n}\) ; p = price relatives = \(\frac{P_{1}}{P_{0}} \times 100\)
Unweighted Geometric mean index number : P01 = Antilog \(\left\{\frac{\sum \log p}{n}\right\}\)
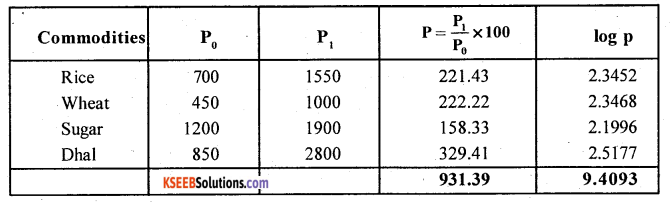
Unweighted Arithmetic Index number : P01 = \(\frac{931.39}{4}\)= 232.85
Unweighted Geometric mean index number : P01 = \(\left\{\frac{9.4093}{4}\right\}\) = AL(2.3523] = 225.07
Question 5.
Calculate price index numbers using un weighted aggregatives of prices method for the years 2012 and 2013 with base 2010 from the following data.
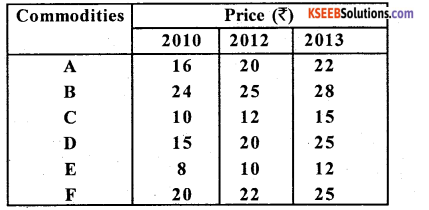
Answer:
Un weightd aggregative price I.NO.
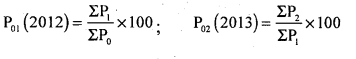
Here:
Base year price of 2010 – P0;
Current year price of 2012 – P1;
Current year price of 2013 – P2;
P01 (2012) = \(\frac{109}{93} \) × 100 = 117.2043 ; P02 (2013) = \(\frac{127}{93} \) x 100 = 136.56.
![]()
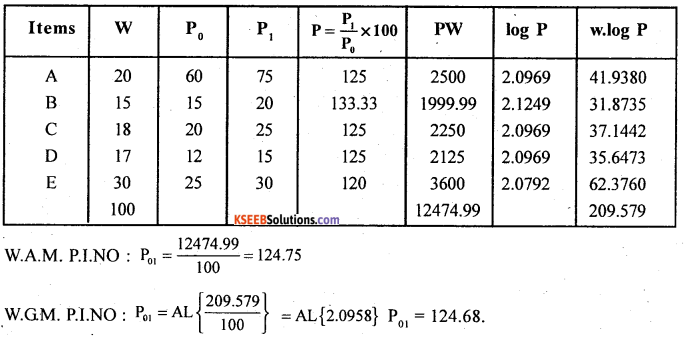
Question 6.
Calculate weighted A.M and weighted and G.M. Index number from the following date.
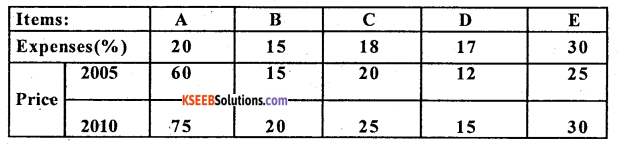
Answer:
Weighted AM. P.1.NO = \(\frac{\Sigma p w}{\Sigma w}\)
Weighted GM. P.LNO = A.L \(\left\{\frac{\Sigma w \cdot \log P}{\Sigma w}\right\}\)
Where P = \(\frac{P_{1}}{P_{0}} \times 100\) – price relatives.
w – weights / Expenses.
Question 7.
Compute suitable quantity index number from the following data.
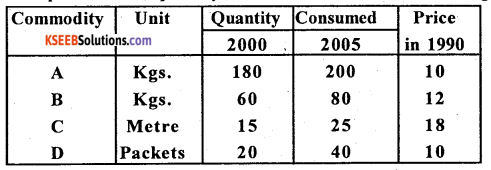
Answer:
Here base year price are given, use Last eyre’s quantity index number.
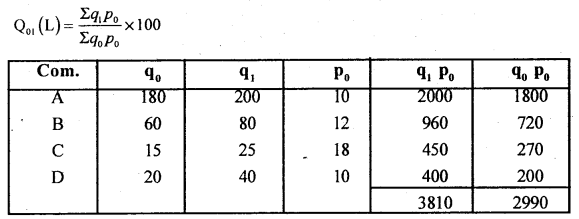
Q10(L) = \(\frac{3810}{2990} \) × 100 = 127.42
Question 8.
Calculate Kelly’s price index number for the following data.
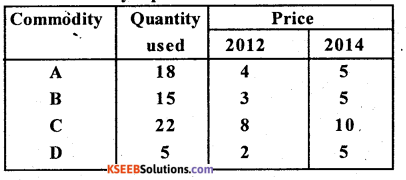
Answer:
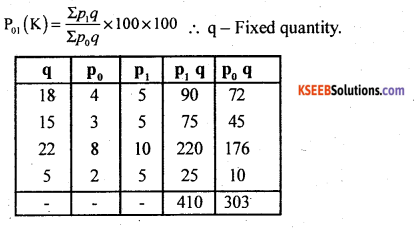
P01 = \(\frac{410}{303}\) × 100 = 135.31
Question 9.
Compute value index number for the year 2012 with respect to base year 2005
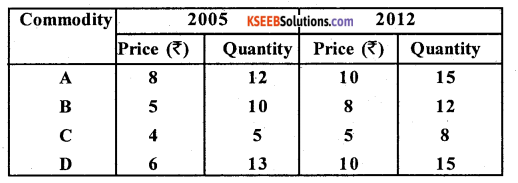
Answer:
Value index number: V01 = \(\frac{\Sigma \mathrm{V}_{0}}{\Sigma \mathrm{V}_{0}} \times 100\)
Here – V1, = P1q1; V0 = p0q0
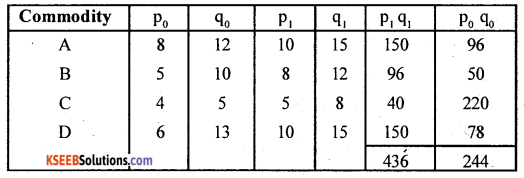
V01 = \(\frac{436}{244}\) × 100 = 178.7
Comment: There is a net increase of transaction (money and quantity together) by 78.7% in the year 2012 as compared to 2005.
Question 10.
Compute consumer price index number using aggregative expenditure method.
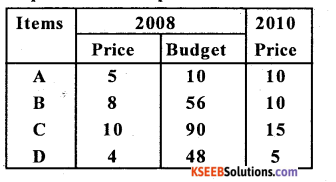
Answer:
C.P.I: I01(A.E.M) = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}} \times 100\) ;
Here budget = p0q0
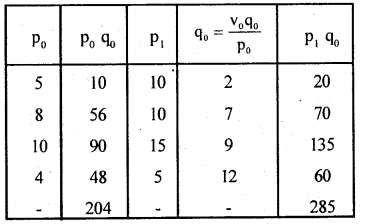
∴ I01 = \(\frac{285}{204} \times 100\) = 139.71
![]()
Question 11.
From the following data construct index fro 2002 taking 2000 as base , by the averange or relative method.
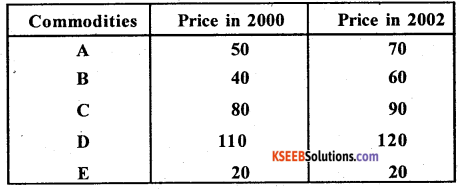
Answer:
Simple A.M. of price relative Index number.
P01= \(\frac{\sum p}{n}\) × 100; P = price relative = \(\frac{P_{1}}{P_{0}} \times 100\)
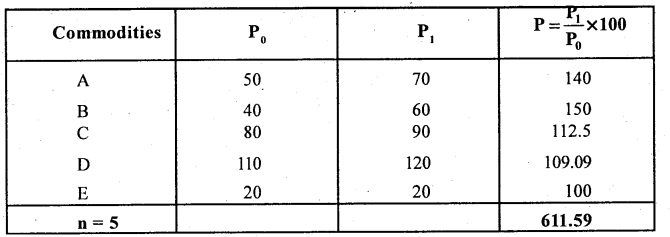
P01 = \(\frac{611.59}{5}\) = 122.32
Question 12.
Construct price Index numbcrs from the following data by applying (a) Laspeyre’s method. (b) Paaschcs method.
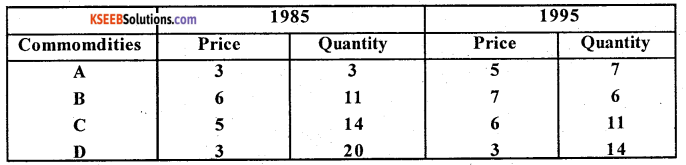
Answer:
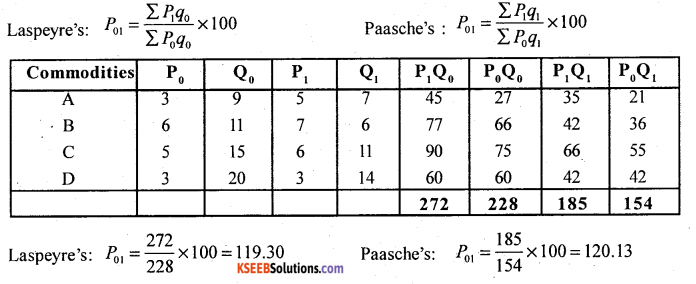
Question 13.
Calculate Paasche’s quantity index number from the following data and give your conclusion.

Ans.
Paasche’s Quantity Index number is- Q01 = \(\frac{\sum q_{1} p_{1}}{\sum q_{o} p_{1}}\) × 100
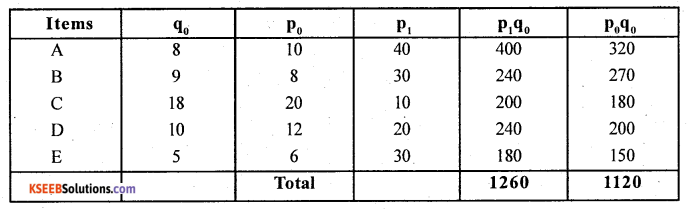
Q01 = \(\frac{1260}{1120}\) × 100 = 112.5
Conclusion: ‘[he quantity level in the current year is 112.5% of the quantity level in the base year.
Question 14.
Calculate Consumer Price Index Number from the following data. Give your conclusion.
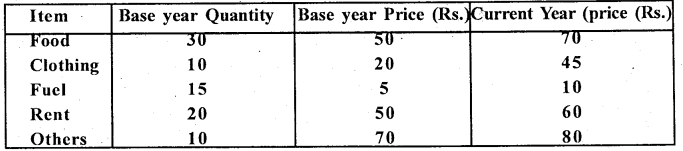
Answer:
Base year quantity (q0) is given, use aggregate expenditure method
Consumer Price Index \( \frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}} \times 100\)
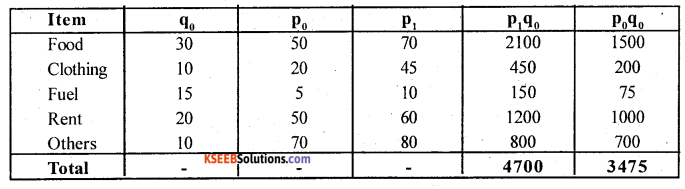
C.P.I. = \(\frac{4700}{3475}\) x 100 = 135.257
Net increase of cost of living in the current year’is 35.257% over the base year.
![]()
Question 15.
Compute Weighted Geometric Mean Index Number from the following data.

Answer:
Weighted geometric mean index number:
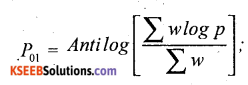
where p = \(\frac{p_{1}}{p_{0}} \times 100\) and w = weight
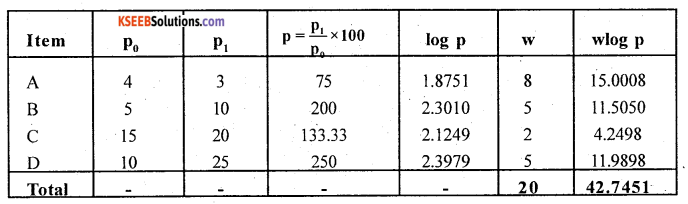
p = Anti log AL \(\left[\frac{42.7451}{20}\right]\) = AL 2.1372 = 137.2
Question 16.
For the following data show that Fisher’s Index Number satisfies Factor Reversal Test :
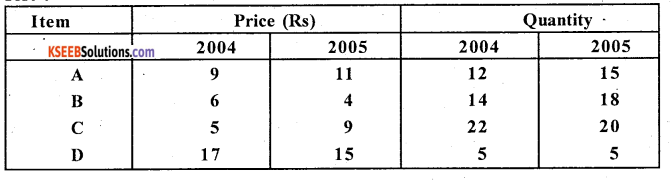
Answer:
Factor Reversal Test = P01 × Q01 = \(\frac{\Sigma \mathrm{P}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{P}_{0} \mathrm{q}_{0}}\) (V01) – (Except 100)
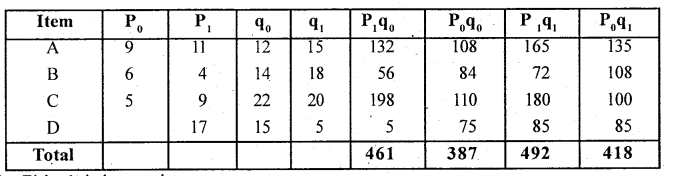
For Fisher’s index number:
L.H.S: P01 x Q01

Fisher’s Index number satisfies F.R.T.
Question 17.
Compute cost of living Index number.
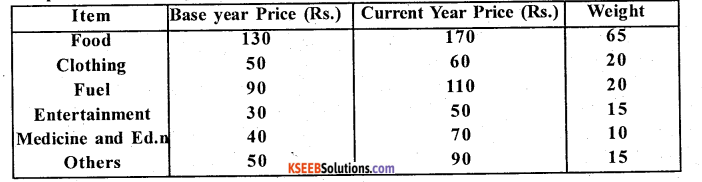
Answer:
Here Weights are given, use Family budget method. C.P.I = \(\frac{\sum P W}{\sum W}\) ; P = \(\frac{P_{1}}{P_{0}} \times 100\)
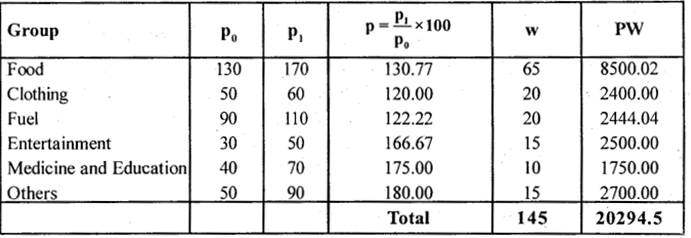
C.P.I = \(\frac{20294.5}{145}\) = 139.96
Question 18.
The following figures relates to the prices and .quantities of certain commodities construct an appropriate Index number.
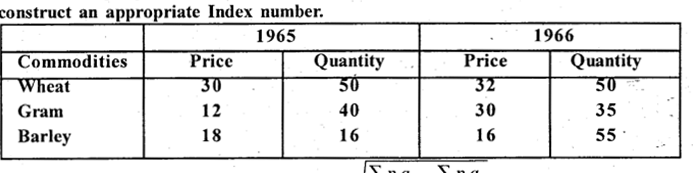
Ans.
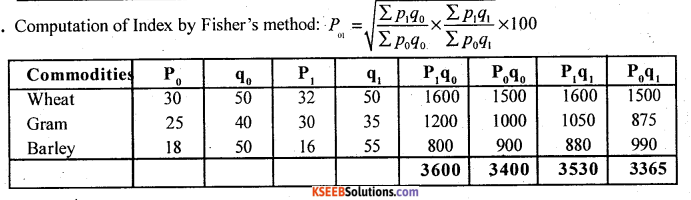
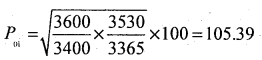
![]()
Question 19.
Construct the cost of living index number by aggregative expenditure method.
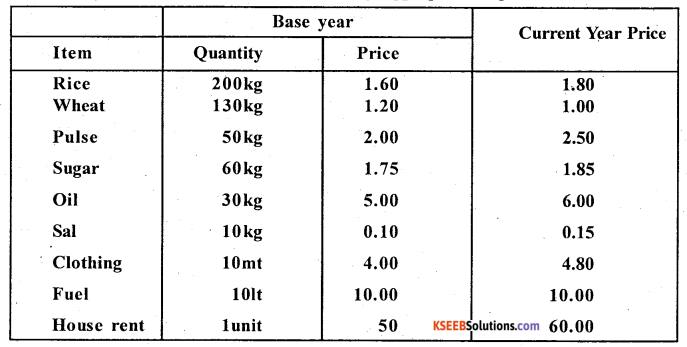
Answer:
Cost of living index number by Aggregate expenditure method ; CPI = \(\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}} \times 100\)
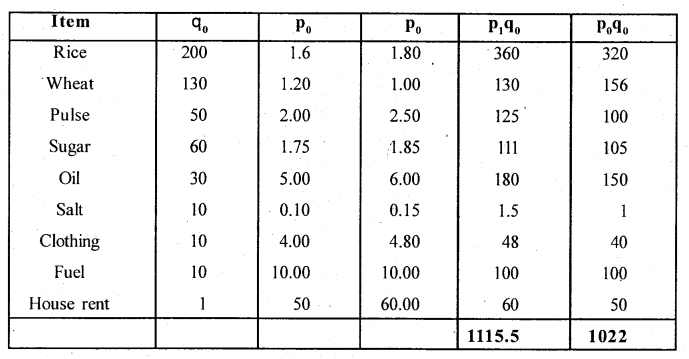
CPI = \(\frac{1115.5}{1022}\) × 100 = 109.15
Question 20.
Construct the cost of living index number for the year 2006.
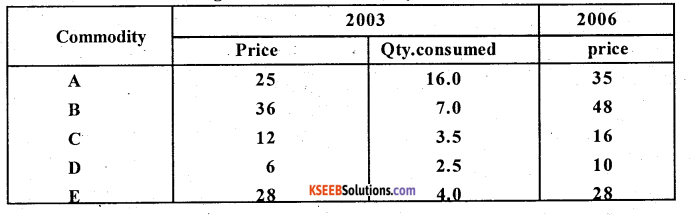
Cost of living index = \(\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}} \times 100\) ; Here base year quantities are given.
So use Aggregative expenditure method.
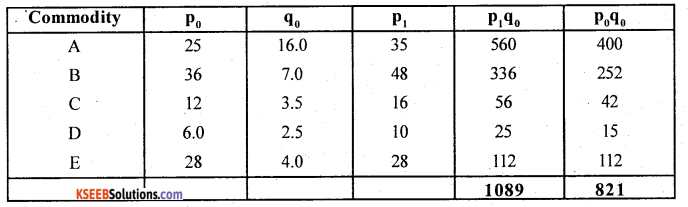
Cost of living index = \(\frac{1089}{821} \times 100\) = 132.64
![]()
Question 21.
Calculate the cost of living index number from the following data.
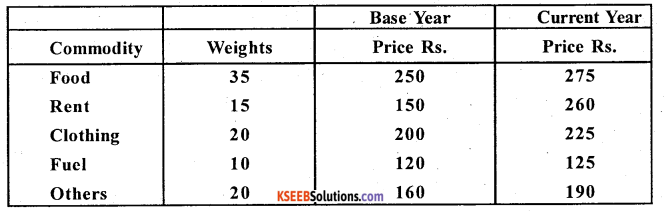
Answer:
Here weights = w is given, are family budget method, CPI = \(\frac{\sum p w}{\sum w}\)
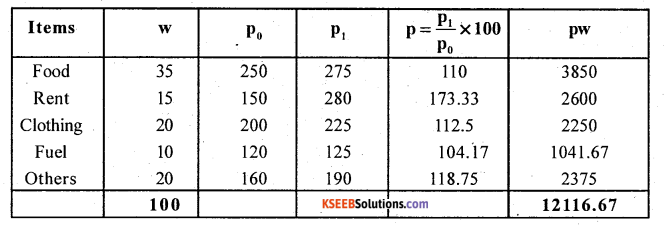
CPI = \(\frac{12116.67}{100}\) = 121.17
Question 22.
Calculate cost of living index number by aggregative expenditure method:
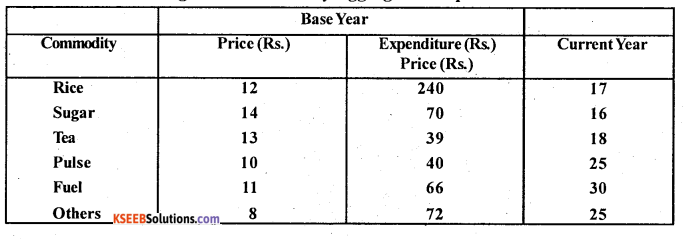
Answer:
Aggregative expenditure method : C.P.I = \(\frac{\sum p_{1} q_{0}}{\sum p_{0} q_{0}}\) x 100.
Here expenditure = P0q0.
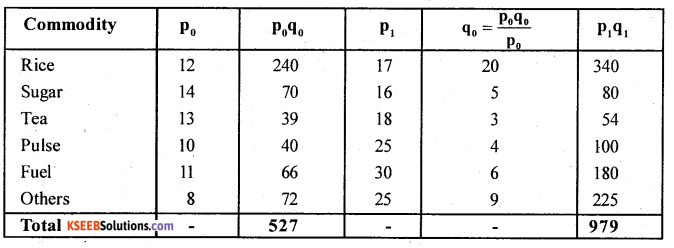
CPI = \(\frac{979}{527} \times 100\) = 185.77
Question 23.
From the following data, construct cost of living index number for the year 1998.

Answer:
Here expense = weights – w : Cost of living index by family budget method.
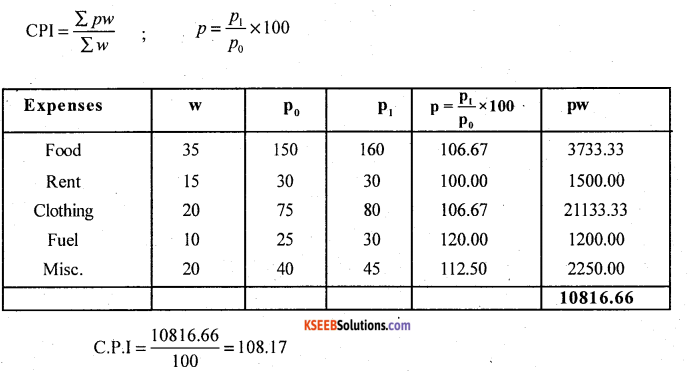
Question 24.
Compute cost of living Index Number:
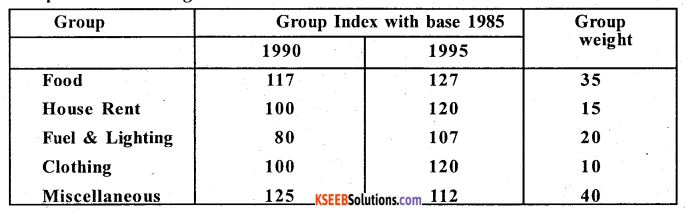
Answer:
Let P and P2 be the group index for the year 1990 and 1995 and w-be the weights. Using family budget method:
CPI (1990) \(\frac{13195}{120}\) = 109.96
CPI (1995) \(\frac{14065}{120}\) = 117.21
2nd PUC Statistics Index Numbers Ten Marks Questions and Answers
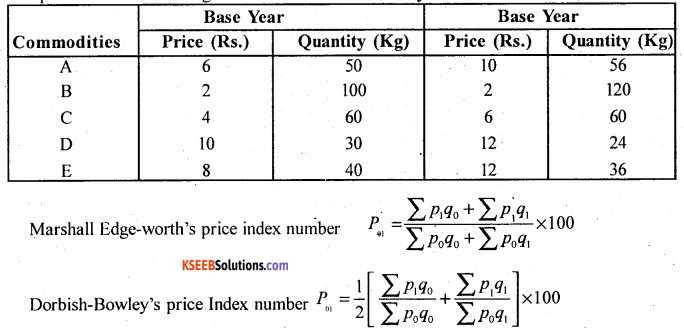
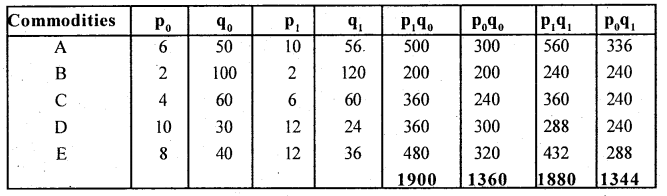
Question 1.
Compute Marshall-Edgeworth’s and Dorbish Bowley’s price Index numbers for the following data.
Answer:
Compution of Marshall-Edgeworth’s and Dorbish-Bowley’s numbers:

![]()
Question 2.
From the data given below construct an Index number of the group of four commodities by using Fisher’s Ideal formula.
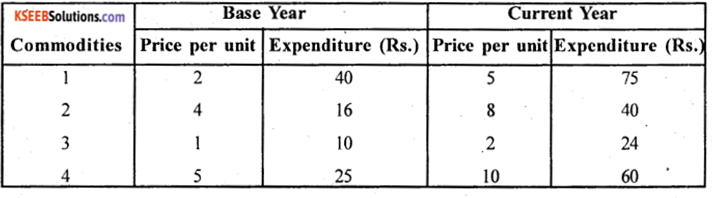
Answer:
Fisher’s Index number
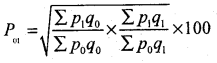
Here Expenditure = p0q0 or p1q1
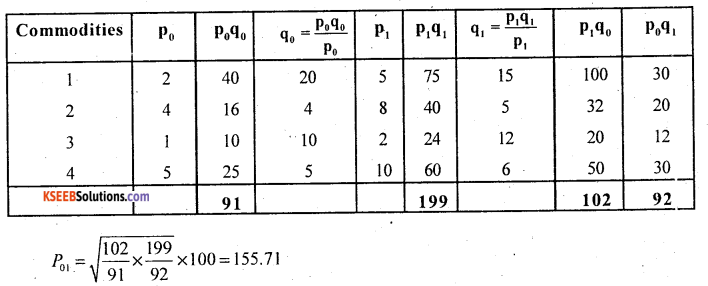
Question 3.
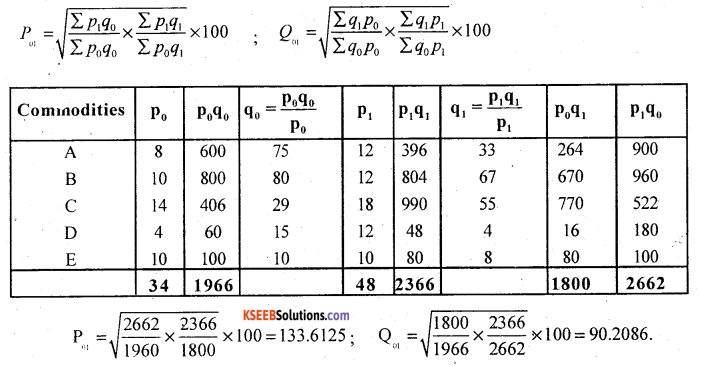
Compute Fisher’s Ideal price and Quantity index numbers for the current year using the following data
Answer:
Computation of Fisher’s price and quantity index numbers,
Question 4.
Calculate Fisher’s Ideal Index number for the following data. Verify that it satisfies time reversal test and factor reversal test.
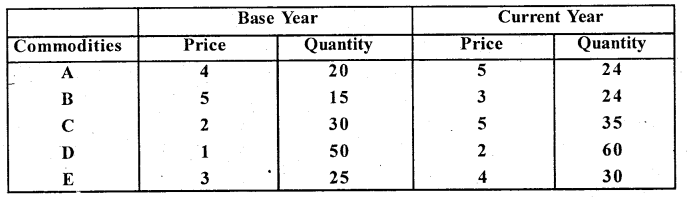
Answer:
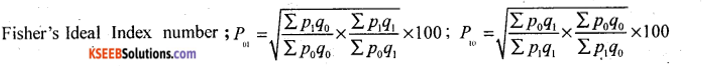
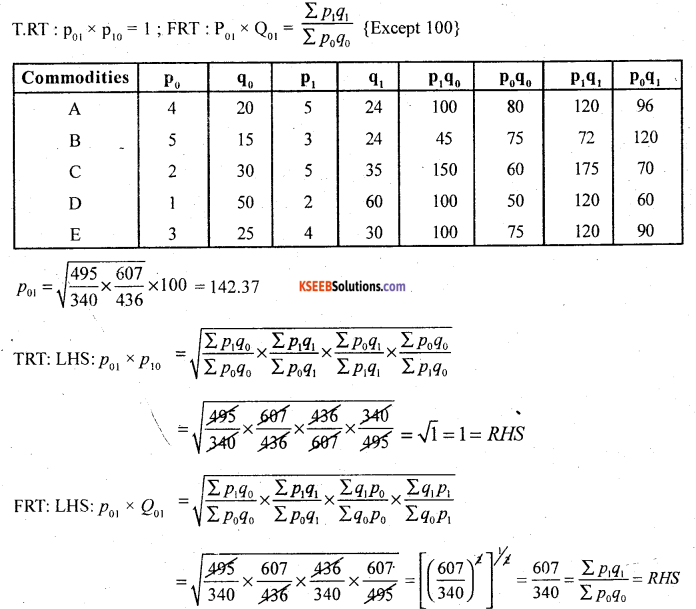
Hence Fishers index number satisfies both time reversal test and factor reversal test.
![]()
Question 5.
Compute ‘Laspeyre’s, Paasches’, Marshall – Edgeworth’s and Fishers quantity Index numbers from the following data.
Answer:
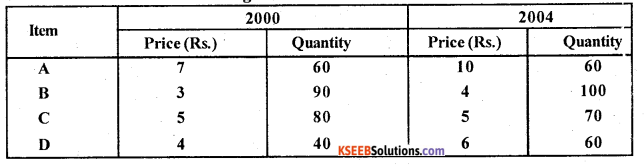
Laspeyre’s:
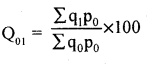
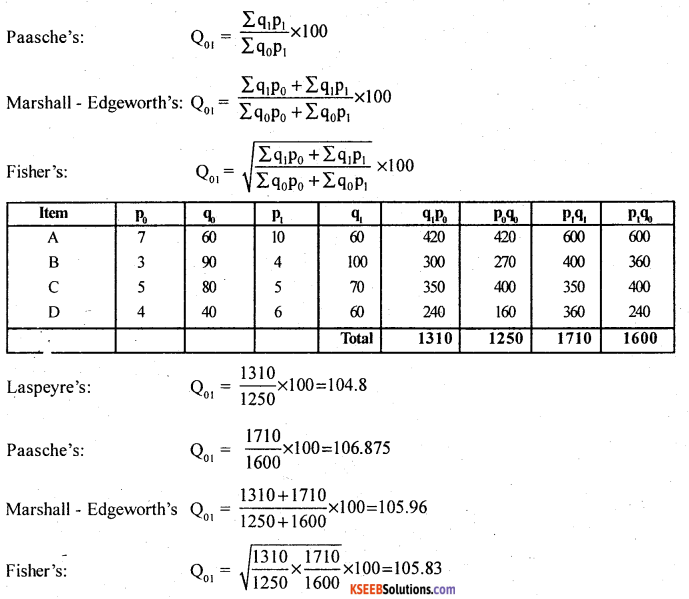
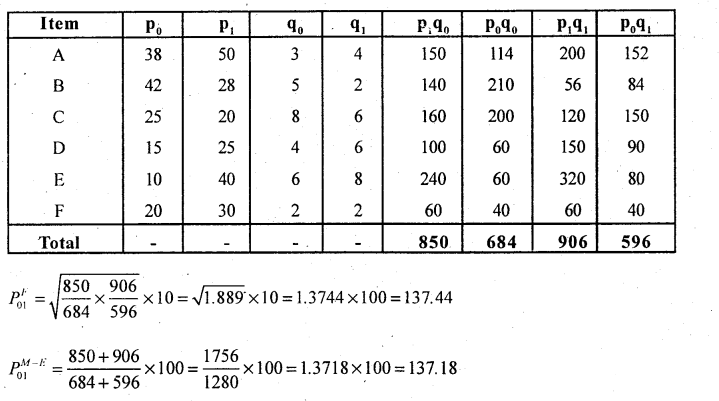
Question 6.
From the following data compute
(i) Fisher’s Price Index number
(ii) Marshall-Edgeworth’s Price Index number. Also show that Fisher’s Price Index number satisfies TRT.
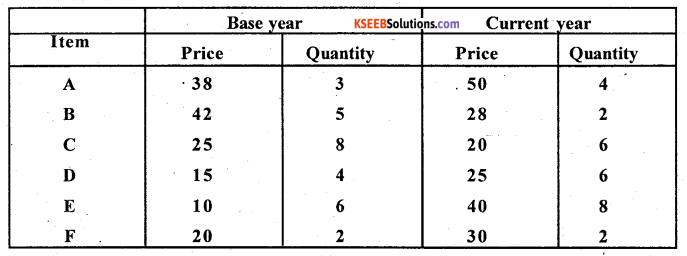
Answer:
Fisher’s Price Index number
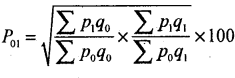
Marshall-Edgeworth’s Price Index number
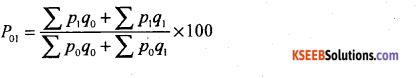
T.R.T = P01 × P10 = 1 (Expect the factor 100)
For Fisher’s: T.R.T : P01 × P10 = 1 Expect 100.