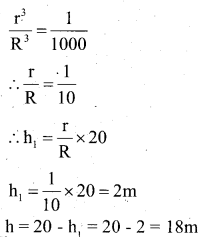Students can Download Karnataka SSLC Maths Model Question Paper 4 with Answers, Karnataka SSLC Maths Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus SSLC Maths Model Question Paper 4 with Answers
Time: 3 Hours
Max Marks: 80
I. In the following questions, four choices are given for each question, choose and write the correct answer along with its alphabet: ( 1 × 8 = 8 )
Question 1.
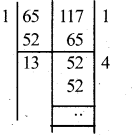
If the H.C.F of 65 and 117 is expressible in the form of 65m – 117, then the value of m is
a) 4
b) 3
c) 11
d) 2
Answer:
Solution:
The H.C.F. of 65 and 117 = 65m- 117
Now 13 = 65m- 117
65m 117+13
65rn = 130
m = 130/65 = 2
∴ The value of m = 2
∴ HCF(65, 117)
= 13
![]()
Question 2.
If sinx = sin 60° cos 30° – cos 60 sin 30!l, then the value of x is
a) 0°
b) 30°
c) 45°
d) 60°
Answer:
b) 30°
Solution:
Sinx = sin 60°cos30 – cos 60 sin 30
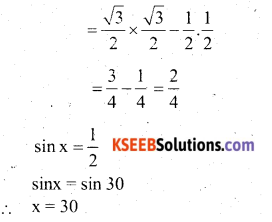
Question 3.
The angle between the radius of a circle and the tangent drawn at the point of contact is
a) 0°
b) 60°
c) 90°
d) 30°
Answer:
c) 90°
Question 4.
The T.S.A. of a cuboid of dimension, l = 30cm, b = 20cm, c = 10cm, is ______
a) 600cm2
b) 60cm2
c) 6000cm2
d) 2200 cm2
Answer:
Question 5.
Which of the following is a polynomial
a) x2 – 5x + 3√x
b) x1/2 + x1/2 – x +1
c) \(\sqrt{x}-\frac{1}{\sqrt{x}}\)
d) x2 – 4x + √2
Answer:
x2 – 4x + √2
Solution:
x2 – 4x + √2 because variable has no negative or decimal powers.
Question 6.
The value of p if x, 2x + p and 3x + 6 are in A.P.
a) p = 3
b) p = 2
c) p = 1
d) p = 0
Answer:
Solution:
x, 2x + p, 3x + 6 are inAP a, A, b are A.P.

2(2x + p) = 2(2x + 3)
2x + p = 2x + 3
p = 2x + 3 – 2k
P = 3
Question 7.
In triangle PQR, The value of y is
a) 4√3
b) 6√3
c) 5√3
d) √3
Answer:
b) 6√3
Solution:
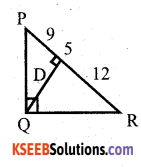
QS2 = PS x SR
QS2 = \(\sqrt{9 \times 12}\)
QS = \(\sqrt{9 \times 4 \times 3}\)
QS = 3 x 2√3
QS = 6√3
Question 8.
When 2 unbiased coins are tossed at ‘ a time, the probability of getting 2 heads is _____
a) 1/4
b) 1/2
c) 1
d) 0
Answer:
a) 1/4
Solution:
S = {(H, H) (H, T) (T, H) (T, T)}
n(s) = 4
An event of getting 2 heads = A={(H, H)}
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{1}{4}\)
![]()
II. Answer the following Questions : ( 1 x 8 = 8 )
Question 9.
If the product of zeros of polynomial f(y) = ay3 – 6y2 + 11y – 6 is 4 then find the value of ‘a’.
Answer:
α β γ = \(-\frac{\mathrm{d}}{\mathrm{a}}\)
4 = \(\frac{-(-6)}{a}\)
4a = 6
a = \(\frac{6}{4}\)
a = \(\frac{3}{2}\)
Question 10.
What is the value of C, if ax2 + bx + c = 0 has equal roots?
Answer:
If ax2 + bx + c = 0 has equal roots then,
b2 – 4ac = 0
b2 = 4ac
4ac = b2
c = \(\frac{b^{2}}{4 a}\)
Question 11.
Find the second term if sum of the ‘n’ term of an AP is 2n2 + 1.
Answer:
Sn = 2n2 + 1
S1 = 2(1)2 + l= 2xl + l= 2+ l= 3
∴ S1 = T1 = a = 3
S2 = 2(2)2 + 1 =8+ 1 =9
a + T2 = 9
T2 = 9 – 3 = 6
Question 12.
State converse of Pythagoras Theorem.
Answer:
“The square on the greatest side of a triangle is equal to the sum of the squares on the other two sides, then the other two sides contian the right angle”.
Question 13.
What is the form of \(\frac{p}{q}\) (p,q ∈ z q ≠ 0) form of 0.57 ?
Answer:
\(0.5 \overline{7}=\frac{57-5}{90}=\frac{52}{90}=\frac{26}{45}\)
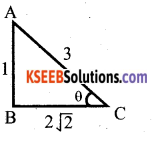
Question 14.
If sinθ = \(\frac{1}{3}\) then find the value of (cot2θ + 2)
Answer:
AC2 = AB2 + BC2
BC2 = AC2 – AB2
= 32 – 12
= 9 – 1 = 8
BC = √8 = 2√2
cotθ = \(\frac{2 \sqrt{2}}{1}\) = 2√2
2cot2θ + 2 = 2(2√2)2 + 2
= 2 x 8 + 2
= 16 + 2
= 18
Question 15.
In sin(A + B) = \(\frac{\sqrt{3}}{2}\) and cos (A – B) = 1, 0< A + B < 90°, A ≥ B
Answer:
sin(A + B) = \(\frac{\sqrt{3}}{2}\) = sin60°
A + B = 60° …. (1)
cos (A – B) = 1 = cos0°
A – B = 0 ….(2)
Solve (1) and (2)
A + B = 60
A – B = 0
2A = 60 or A = 30°
A + B = 60
30 + B = 60
B = 60 – 30° = 30°
∴ A = 30°, B = 30°
![]()
Question 16.
The surface area of a sphere is same as the C.S.A. of a right circular cylinder whose height and diameter are 4 cm each. Find the radius of the sphere.
Soln:
4πr² = 2πrh
4R² = dh .
4R²= 4 x 4
R² = \(\frac{4 \times 4}{4}\) = 4
R = √4 = 2cm
A = 30°, B = 30°
∴ Radius of the sphere = 2cm.
III. Answer the following : ( 2 x 8 = 16 )
Question 17.
By Euclid’s division lemma, show that thte square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Answer:
Let x be any positive integer. Then it is of the form 3q, 3q+1 or 3q + 2.
Now, (3q)2 = 9q2 = 3(3q2) = 3m where m = 3q2
(3q + 1)2 = 9q2 + 6q+ 1 = 3(3q2 + 2q) + 1
= 3m + 1, where m = 3q2 + 2q and (3q+2)2 = 9q2 + 12q + 4
= 3(3q2 + 4q + 1) +1
=3m +1, where m = 3q2 + 4q + 1
Hence, it is proved.
Question 18.
Solve : \(\frac{x+y}{x y}\) = 2 and \(\frac{x-y}{x y}\) = 6
Answer:
x + y = 2xy
x – y = 6xy
2x = 8xy
2 = 8y

Question 19.
Solve : y2 – (√3 + 1)y + √3 = 0
Answer:
y2 – √3y – y + √3 = 0
y(y – √3) – 1(y – √3) = 0
(y – √3)(y – 1) = 0
y – √3 = 0, y – 1 = 0
y = √3 and y = 1
![]()
Question 20.
Show that the points (3, 2) (-2, -3) and (2, 3) are collinear Or non – collinear.
Answer:
Let A= (3, 2) B = (-2, -3) C = (2, 3)
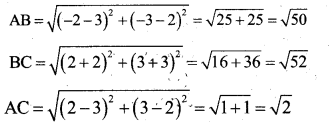
AC ≠ AB + BC
∴ They are non – collinear.
Question 21.
In the given fig ∆DGH ~ ∆DEF, DH = 8cm, DF = 12cm, DG = (3x – l)cm and DE = (4x +. 2)cm, Find the lengths of DG and DE.
Answer:
∆DGH ~ ∆DEF
\(\frac{\mathrm{DG}}{\mathrm{DE}}=\frac{\mathrm{DH}}{\mathrm{DF}}\)
\(\frac{3 x-1}{4 x+2}=\frac{8}{12}\)
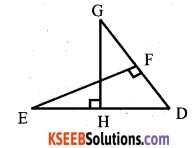
12 (3x – 1) = 8(4x + 2)
36x – 12 = 32x + 16
36x – 32x = 16 + 12
4x = 28
x = 28/4
x = 7
∴ DG = 3x – 1 = 3 x 7 – 1 = 21 – 1 = 20
DE = 4x + 2 = 4 x 7 + 2 = 28 + 2 = 30
OR
D is a point on the side BC of A ABC such that ∠ADC = ∠BAC. Prove that
\(\frac{\mathbf{C A}}{\mathbf{C D}}=\frac{\mathbf{C B}}{\mathbf{C A}}\)
Answer:
In ∆ ABC and ∆ DAC,
∠ADC = ∠BAC and
∠C = ∠C
∆ABC ~ ∆DAC
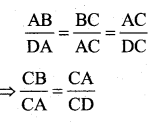
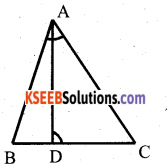
Question 22.
A card is drawn at random from a box containing 21 cards numbered 1 to 21. Find the probability that the card drawn is
a) Prime number b) Divisible by 3.
Answer:
n(s) = 21
A= {2,3,5,7,11,13,17,19}
n(A) = 8
P(A) = \(\frac{n(A)}{n(S)}=\frac{8}{21}\)
b) n(S) = 21
B= {3,6, 9,12,15,18}
n(B) = 6
∴ P(B) = \(\frac{n(B)}{n(S)}=\frac{6}{21}=\frac{2}{7}\)
Question 23.
Draw a circle of radius 3cms. Construct a pair of tangents to it, from a point 5cm away from the circle.
Answer:
r = 3cm d = 3 + 5 = 8cm
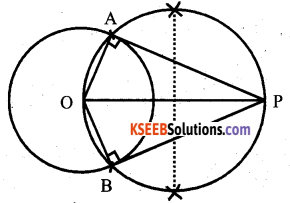
Question 24.
Express sinA and sec A in terms of cot A.
Answer:
W.K.T cosec2A = 1 + cot2A
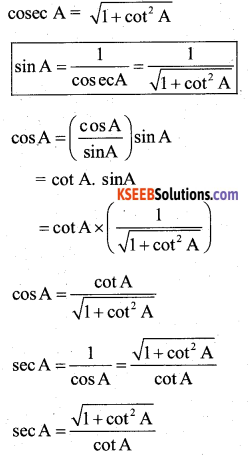
OR
If tanθ + sinθ = m and tan θ – sin θ= n, S.T m2 – n2 = 4\(\sqrt{\mathbf{m} \mathbf{n}}\)
Answer:
L.H.S = m2 – n2 = (m +n) (m – n)
= {(tan θ + sin θ ) + (tan θ – sin θ )x(tan θ +sin θ) – (tan θ – sin θ)}
= {(2tanθ) x (2sinθ) = 4tanθsinθ

= 4\(\sqrt{\mathbf{m} \mathbf{n}}\)
= RHS.
IV. Answer the following : ( 3 x 9 = 27 )
Question 25.
The sum of the numerator and denominator of a fraction is 24. If 4 is subtracted from the numerator and 5 from its denominator, then it reduces to 1/4. Find the fraction.
Answer:
Let the fraction be \(\frac{\mathrm{x}}{\mathrm{y}}\)
sum of its numerator and denominator = 24.
x + y = 24 ……..(1)
If 4 is subtracted from the numerator and
5 from its denominator we get = 1/4
⇒ \(\frac{x-4}{y-5}=\frac{1}{4}\)
4(x – 4) = 1(y – 5)
4x – 16 = y – 5
4x – y = -5 + 16
4x – y = 11 ……..(2)
From (1) and (2)
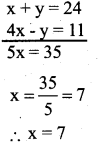
Consider,
x + y = 24
7 + y = 24
y = 24 – 7
y = 17
∴ The fraction is \(\frac{x}{y}=\frac{7}{17}\)
OR
Two women and five men can together finish an embroidary work in 4 days. While three women and 6 men can finish in 3 days. Find the time taken by one women alone and also that taken by one man alone.
Answer:
Let 1 woman can finish the embroidary in x days and 1 man can finish the embroidary in y days.
1 woman’s 1 day’s work = \(\frac{1}{x}\)
1 man’s 1 day’s work = \(\frac{1}{y}\)
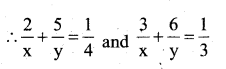
Let \(\frac{1}{x}\) = u, \(\frac{1}{y}\) = v
2u + 5v = \(\frac{1}{4}\)
3u + 6v = \(\frac{1}{3}\)
solve (1) and (2)
(8u + 20v = 1) x 9
(9u+ 18v= 1) x 8
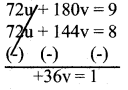
v = \(\frac{1}{36}\)
Put v = \(\frac{1}{36}\)…….(1)
2u + 5v = \(\frac{1}{4}\)
2u + 5\(\frac{1}{36}\) = \(\frac{1}{4}\)

Thus, 1 woman alone can finish the embroidery in 18 days and 1 man alone can finish it in 36 days.
![]()
Question 26.
If two zeroes of the polynomial p(x) = x4 – 6x3 – 26x2 + 138x – 35 are 2 – √3 and 2 + √3. Find the other two zeroes.
Answer:
The two zeroes of p(x) are,
(2 – √3) and (2 + √3)
⇒ [x – (2 – √3] and [x – [2 + √3] are the factors p(x).
⇒ [ x – 2 + √3] [x – 2 – √3]
(x – 2)2 – (√3)2
x2 – 4x + 4 – 3
⇒ x2 – 4x + 1 is a factor of p(x)
Divide p(x) by x2 – 4x + 1 to get quotient

Consider the quotient, x2 – 2x – 35 = 0
x2 – 7x + 5x – 35 = 0
x(x – 7) + 5(x – 7) = 0
(x – 7) (x + 5) = 0
x-7 = 0 orx + 5 = 0
x = 7 or x = -5
∴ The other two zeroes are 7, -5.
Question 27.
A two digit number is such that the product of its digits is 18. when 63 is subtracted from the number, the digits interchange their places. Find the number.
Answer:
Let the two digits be x and y.
⇒ The two digit number is = 10x + y
The product of three digits = xy = 18
When 63 is subtracted from the number, the digits interchange their places.
10x + y – 63 = 10y + x
10x – x – 10y + y = 63
9x – 9y = 63
9(x – y) = 63
x – y = 63/9 = 7
x – y = 7
x = 7 + y
Consider xy = 18 and substitute x = (y + 7) in it.
y(y + 7) = is . .
y2 + 7y – 18 = 0
y2 + 9y – 2y – 18 = 0
y (y + 9) – 2(y + 9) = 0 –
(y + 9) (y – 2) = 0 .
y + 9 = 0, y -2 = 0
y = -9 or y = 2
xy= 18
x(2) = 18
x = 18/2 = 9
x = 2
But negative digit is not considered.
∴ The two digit number is
= 10x + y
= 10(9) + 2 = 92
OR
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km away in time it has to increase its speed by 250 km / hr from its usual speed. Find its usual speed.
Answer:
Let the usual speed of the plane be x km / hr. Time taken to cover 1500 km with the usual speed.
\(\frac{1500}{x}\) hrs
Time taken to cover 1500 km with the speed of (x + 250) km / hr = \(\frac{1500}{x+250}\)

2(1500 x 250) = x2 + 250x
x2 + 250x-750000 = 0
x2 + 1000x – 750x – 750000 = 0
x(x + 1000) – 750(x + 1000) = 0
(x+ 1000)(x-750) = 0
x + 1000 = 0 or x – 750 = 0
x = -1000 or x= 750 ,
x = 750
Hence, the usual speed of the plane = 750 km/hr.
![]()
Question 28.
If the co – ordinates of the mid points of ∆ ABC are D(1, 2) E(0, -1) and (2, -1). Find the respective co – ordinates of ∆ ABC.
Answer:
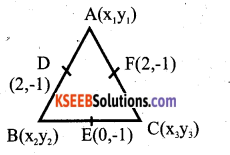
D is the midpoint of BC.
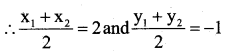
x1 + x2 = 4 and y1 + y2 = -2 ………(1)
E is the mid point of BC
![]()
x2 + x3 = 0 and y2 + y3 = -2 …….(2)
F is the mid point of BC
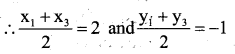
x1 + x3 = 4 and y2 + y3 = -2 ….(3)
Solve (1) and (3)
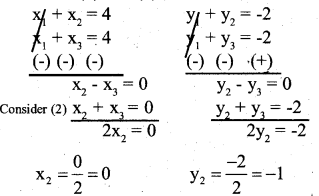
x2 = 0
x2 = 0
0 + x3 = 0
x3 = 0
x1 + x3 = 4
x1 + 0 = 4
x1 = 4 – 0 = 4
x1 = 4
y2 = -i
y2 + y3 = -2
-1 + y3 = -2
y3 = -2 +1
y3 = -1
y1 + y3 = -2
y1 + (-1) = -2
y1 -1 = -2
y1 = -2 + 1 = -1
y1 = -1
A(x1,y1) = A(4,-1)
B (x2 y2) = B(0, -1)
C(x3, y3) = C(0,-1)
OR
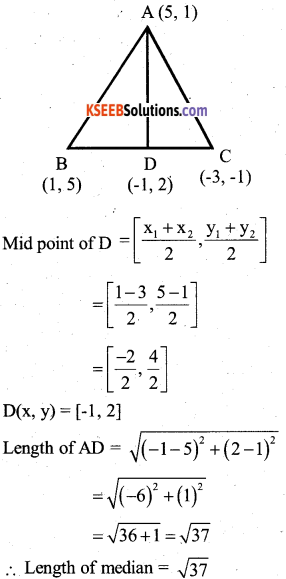
Find the length of the median through the vertex A(5,1) drawn to the triangle ABC where other two vertices are B(1, 5) andiC(-3, -1)
Answer:
Question 29.
Prove that the tangents drawn from an external point are equal.
Answer:
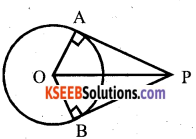
Data : ‘O is the centre of the circle PA and PB are the two tangents drawn from an external point P. OA and OB are radii of the circle.
To prove that : ∠APB + ∠AOB = 180°
∠OAP + ∠OBP = 90°
(∵ Angle between the radius and tangent at the point of contact is 90°)
OP = OP (Common side)
OA = OB (Radii of the same circle)
According to RHS postulate
∆APO = ∆BPO
∠ OAP = ∠OBP = 90°
∠OAP + ∠OBP = 90° +90° =180°
⇒ Opposite angles of OAPB quadrilateral are supplementary.
OAPB is a cyclic quadrilateral
⇒ ∠ APB + ∠ AOB = 180°
![]()
Question 30.
If a chord of circle of radius 10cm subtend an angle of 60° at the centre of the circle. Find the area of the corresponding segment of the circle.
(Take π =3.14, √3 = 1.7)
Answer:
O is the centre of the circle having radius 10 cm.
∠ AOB = 60° is angle subtended at the centre O of the circle by a chord AB.
Draw BL ⊥ OA
In right angled ∆ OLB,

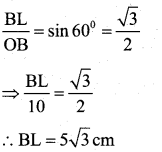
Area of segment ∆ APB
= The area of sector OAPB – Area of ∆ OAB

OR
Find the area of the shaded region where PQRS is a square of side lOcms and semicircles are drawn with each side of square as diameter.
Answer:
The four shaded regions are marked as I, II, III, IV.
All the four regions have equal areas due to § symmetry.
Area of I + Area of III
= Area of square ABCD – Sum of the areas of two semicircles of each of radius 5cm.
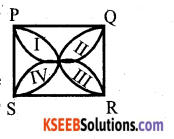
{10 x 10 – 2 x \(\frac{1}{2}\) π x 52}cm2
= {100 – 25 x 3.14} cm2
= {100 – 78.5} cm2
= 21.5 cm2
Similarly Area of II + Area of IV = 21.5 cm2. Total Area of shaded region = 21.5 + 21.5
= 43 cm2
Question 31.
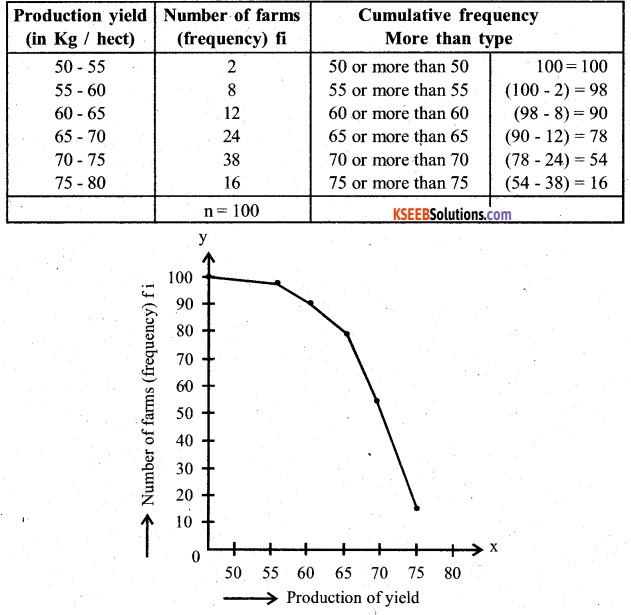
The following table gives the production yield per hectare of paddy of 50 farms of a village.

Answer:
Question 32.
Find the mean of the following frequency distribution.

Answer:

A = 50, h = 20, N = 100 and Σ fiui = 15
Mean = A + h\(\left\{\frac{1}{\mathrm{N}} \sum \mathrm{f}_{i} \mathrm{u}_{\mathrm{i}}\right\}\)
Mean = 50 + 20 x \(\frac{15}{100}\)
Mean = 50 + 3 = 53
![]()
Question 33.
Construct a triangle of sides 4cm, 5cm and 6cm and then a triangle similar to it whose Sides are 2/3 of the corresponding sides of it.
Answer:
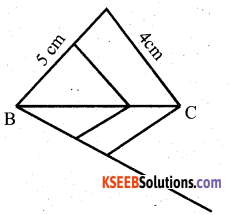
V. Answer the following : ( 4 x 4 = 16 )
Question 34.
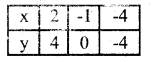
Solve the pair of equations graphically.
4x – 3y + 4 = 0
4x + 3y – 20 = 0
Answer:
4x – 3y + 4 = 0 ….. (1)
4x + 4 = 3y
y = \(\frac{4 x+4}{3}\)
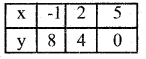
4x + 3y – 20 = 0
3y = -4x + 20
y = \(\frac{-4 x+20}{3}\)
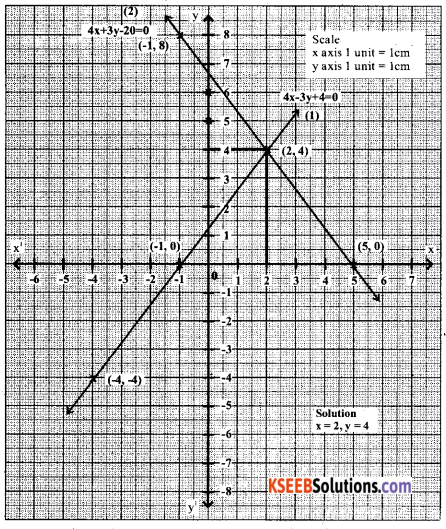
Question 35.
How many terms of the series 93 + 90 + 87 + ……….. amounts to 975. Find also the last term.
Answer:
93 + 90 + 87 + …………
a = 93, d = 90 – 93 = -3, Sn = 975, n = ?,
T = ?
S = \(\frac{n}{2}\)[2a + (n – 1)d]
975 = \(\frac{n}{2}\)[2(93) + (n-1)(-3)]
975 x 2 = n[186 – 3n + 3]
1950 = n [189 – 3n]
1950 = n[189 – 3n]
1950 = 189n – 3n2
(3n2-189n+ 1950-0) H-3
n2 – 63n + 650 = 0
n2 – 50n-13n +650 = 0
n(n – 50) – 13(n – 50) = 0
(n – 50) (n -13) = 0
n – 50 = 0 or n – 13 = 0
n= 50 or n= 13
When n = 50, the last term
Tn = a + (n – 1)d
= 93 + (49) (-3)
= 93 – 147
T50 =-54
When n = 13, the last term
Tn = a + (n – 1)d ”
=93 + (13-1) (-3)
= 93 – 36
T13 = 57
OR
If m times the mth term of an A.P is equal to n times its n,h term, show that (m + n)th term is zero.
Soln: Let T1 = a and c.d = d
Given : m times m,h term = n times nthterm
=> mTm = nTn
m[a + (m – 1)d] = n[a + (n – 1)d]
m[a +(m – l)d] – n[a+(n -l)d] = 0
m[a + md – d] – n[a + nd – d] = 0
ma + m2d – md – na – n2d + nd = 0
a(m – n) + d(m – n) (m + n) – d(m – n) = 0
(m – n) {a + d(m +n) – d} = 0 . (m – n) {a + (m + n – l)d} = 0
m-n = 0, a + (m + n-l)d = 0
m= n Tm+n , = 0
But m ≠ n
Question 36.
A tower is 50m high. Its shadow is x mtrs shorter when the suns altitude is 45° than when it is 30°. Find the value of x.
Answer:
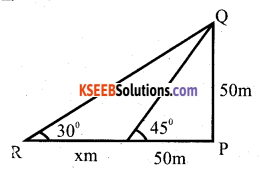
Let PQ be the tower and let PA and PB be its shadows when the altitudes of the sum are 45° and 30° respectively.
∠ PAQ = 45°, ∠ PBQ = 30°
∠ BPQ = 90° and PQ = 50m ,
Let AB = x metres
From right angled ∆ APQ, we have
\(\frac{\mathrm{AP}}{PQ}\) = cot 45°=1
\(\frac{\mathrm{AP}}{50}\) = 1 => AP = 50m
From right angled ∆ BPQ,
\(\frac{\mathrm{BP}}{\mathrm{PQ}}\) = cot30° = √3
⇒ \(\frac{x+50}{50}\) = √3
x = 50(√3 – 1)m
= 50 (1.73 – l)m
= 50 x 0.732
= 36.6 m
Question 37.
Prove that “In a right angled triangle, square on the hypotenuse is equal to sum of the squares on the other sides.”
Answer:
Verify
BC = 8cm
BC’= \(\frac{5}{3} \times 8=\frac{40}{3}\)
AB =6cms
A’B= \(\frac{5}{3} \times 6\)
=10cms.
![]()
VI. Answer the following : ( 5 x 1 = 5 )
Question 38.
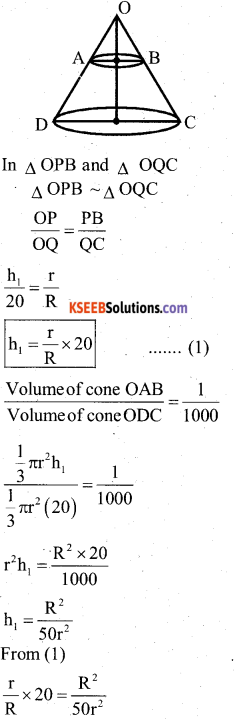
The height of cone is 20m. A small cone is cut off from it at its top by the plane parallel to the base. If the volume of small cone 1/1000 th of the volume of given cone, at what height above the base the section is made.
Answer:
In A OPB and A OQC A OPB ~aOQC OP _ PB OQ ~ QC