Students can Download Maths Chapter 11 Congruency of Triangles Ex 11.6 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 11 Congruency of Triangles Ex 11.6
Question 1.
Suppose ABCD is a rectangle. Using RHS theorem prove that the triangles ABC and ADC are congruent.
Answer:
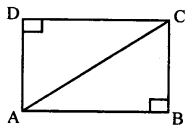
In ∆ ABC and ∆ ADC
∠ABC = ∠ ADC = 90°
[Angles of a rectangle]
AC = AC [Common side]
AB = DC [Opposite side rectangle]
∴∆ ABC = ∆ ADC [RHS theorem]
Question 2.
Suppose ABC is a triangle and D is the midpoint of BC. Assume that the perpendiculars from D to AB and AC are of equal length. Prove that ABC is isosceles.
Answer:
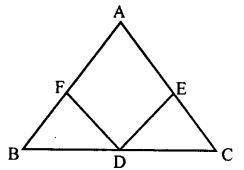
DF ⊥ AB and DE ⊥ AC
In ∆BFD and ∆CED
∠BFD = ∠ CEP [= 90° by data]
BD = DC [D is the midpoint of BC]
DF = DE[data]
∴ ∆ BFD ≅ ∆CED [RHS theorem]
∴∠B =∠C [Corresponding angles]
∴AC = AB [Theorem 2]
Question 3.
Suppose ABC is a triangle in which BE and CF are respectively the perpendiculars to the sides AC and AB.
If BE = CF. Prove that triangle ABC is isosceles.
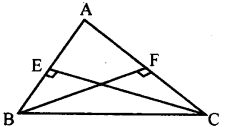
Answer:
In ∆ BFC and ∆ BEC
∠BFC = ∠BEC [= 90° data]
BC = BC [Common side]
CF = BE [data]
∴ ∆BFC ≅ ∆BEC [RHStheorem]
∠EBC = ∠FCB [Corresponding angle]
i. e., AB = AC
∴ ∆ ABC is isosceles