Students can Download Maths Chapter 3 Axioms, Postulates and Theorems Ex 3.2 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka Board Class 8 Maths Chapter 3 Axioms, Postulates and Theorems Ex 3.2
I. Draw diagrams illustrating each of the following situations
Question a.
Three straight lines which do not pass through a fixed point.
Answer:
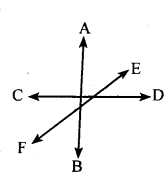
Question b.
A point and rays emanating from that point such that the angle between any two adjacent rays is an acute angle.
Answer:
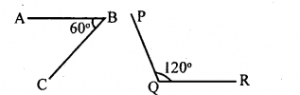
Question c.
Two angles which are not adjacent angles, but still supplementary.
Answer:
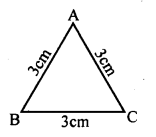
Question d.
Three points in the plane which are equidistant from each other.
Answer:
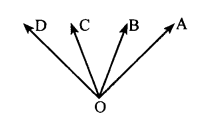
Question 2.
Recognise the type of angles in the following figures.
Answer:
i. Adjacent angles
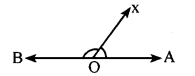
AOX is an acute angle and BOX is an obtuse angle
ii. Exterior angles
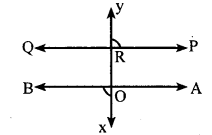
PRY and BOX are supplementary angles
iii. Reflex angle
Question 3.
Find the value of ‘x’ in each of the following diagrams.
(i) x + 2x = 180°
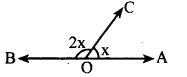
Answer:
3x = 180°
x = \(\frac{180^{\circ}}{3}\) = 60°
∴ x= 60°
(ii) ∠COB = 90°
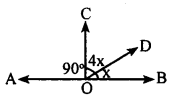
∠COD +∠DOB = 90°
4x + x=90°
5x = 90
x = \(\frac { 90 }{ 5 }\)
x = 18°
∠AOC + ∠COB + ∠BOD + ∠DOA = 360° Complete angle
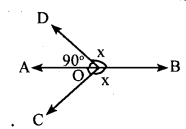
∠ AOC + x + x +∠ DOA = 360°
90 + 2x = 360° [∠ AOC +∠DOA = 90° ]
2x = 360 – 90
2x = 270
x = \(\frac { 270 }{ 2 }\)
x = 135°
(iv) ∠AOB = 180°
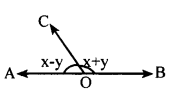
∠AOC + ∠BOC = 180°
x – y + x + y = 180°
2x = 180°
x = \(\frac { 180 }{ 2 }\)
x = 90°
(v) ∠COF= ∠EOD
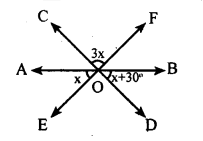
∠COF = 3x
∴∠EOD = 3x
∠AOB = 180°
∠AOE + ∠EOD + ∠DOB = 180°
x + 3x + x + 30 = 180°
5x + 30 = 180°
5x = 180 – 30
5x = 150
x = \(\frac { 150 }{ 5 }\)
x = 30°
(vi)
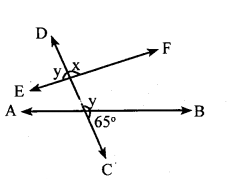
EF is a straight line
∴ x + y = 180° ………..(i)
DC is a straight line
∴ y+ 65° = 180° …(ii)
From(i)and(ii)
x + y = y + 65°
x + y – y = 65°
x = 65°
Question 4.
which pair of angles are supplementary in the following diagram ? Are they supplementary rays ?
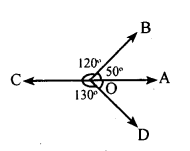
Answer:
∠AOB and ∠COD are supplementary angles.
∠COB and ∠AOD are supplementary angles.
There are no supplementary rays in the diagram.
Question 5.
Suppose two adjacent angles are supplementary. Show that if one of them is an obtuse angle, then the other angle must be acute.
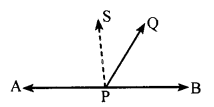
Answer:
In the figure
∠APQ + ∠BPQ = 180° and ∠APQ is an obtuse angle.
To prove ∠BPQ < 90°
Construction: Draw a perpendicular SP at P
Proof: In the fig
∠ APS +∠SPQ + ∠QPS = 180°
90 + ∠SPQ + ∠QPB = 180°
∠SPQ + ∠QPB = 180-90
∠SPQ +∠QPB = 90
∴∠SPQ < 90° and ∠QPB < 90°
∴∠QPB is an acute angle
∴∠APQ is an obtuse angle