KSEEB Solutions for Class 9 Maths Chapter 6 Constructions Ex 6.1 are part of KSEEB Solutions for Class 9 Maths. Here we have given Karnataka Board Class 9 Maths Chapter 6 Constructions Exercise 6.1.
Karnataka Board Class 9 Maths Chapter 6 Constructions Ex 6.1
Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
Data: Constructing an angle of 90° at the initial point of a given ray.
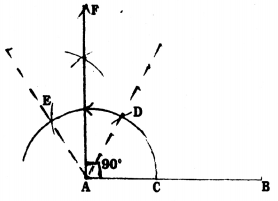
Steps of Construction:
- Draw AB straight line.
- Taking A as centre and any radius draw an arc and intersect AB at C.
- Taking C as centre with the same radius draw an arc which intersects at D.
- With the same radius taking D as centre, it intersects at E.
- With centres E and D with the same radius draw two arcs which meet both at F.
- If AF is joined, AB straight line is the line in point A with 90°, i.e., AF.
In the above construction ∠DAB = 60° and ∠DAE = 60°.
Angular bisector of ∠DAE is AF.
∴ ∠DAF = ∠EAF = 30°
∴∠BAF = ∠DAB + ∠DAE = 60°+ 30°
∴∠BAF = 90°.
Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
Data: To construct an angle of 45° at the initial point of a given ray.
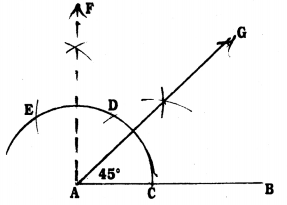
Steps of Construction :
- Draw a straight line with any measurement.
- Taking A as centre with any radius draw an arc, which meets AB at C.
- With C centre, with the same radius draw an arc which meets at D.
- With D centre, with the same radius, draw an arc which meets at D.
- With centres E and D, with the previous radius draw two arcs which meet at F.
- Now AF is joined. Now AP1AF at A. Hence ∠BAF = 90°.
- Now, AG which is the angular bisector of ∠BAF is drawn.
- ∠BAG = 45° is constructed.
∠FAB = 90°
AG is the angular bisector of ∠FAB
∴ ∠FAG = ∠GAB = 45°
∴ ∠GAB = 45°.
Question 3.
Construct the angles of the following measurements :
(i) 30°
(ii) \(22 \frac{1}{2}^{\circ}\)
(iii) 15°.
Solution:
(i) To construct 30° angle :
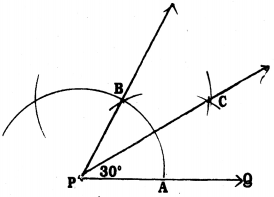
Steps of Construction :
- Draw PQ straight line.
- With P as centre with any radius draw \(\frac{1}{2}\) arc- intersects PQ at A.
- With A as centre with the same radius draw an arc which intersects at B. Join PB and produced.
- With A and B centres, with radius more than half of AB draw two arcs which intersect at C. Join PC.
- ∠BPC = ∠CPQ = 30°.
(ii) To draw an angle of \(22 \frac{1}{2}^{\circ}\)
Solution:
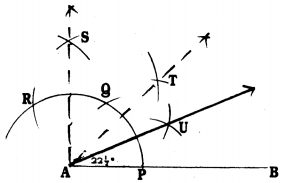
Steps of Construction:
- Draw a straight line AB.
- With centre ‘A’, taking a convenient radius to draw an arc which intersect AB at P.
- With P as centre with the same radius draw an arc at Q, with Q as centre with the same radius draw an arc which intersects at R.
- With R and Q centres with the same radius draw two arcs which intersect at S. Join AS, ∠BAS = 90°.
- Now construct AT which is the angular bisector of ∠BAS, and joined, ∠TAB= 45°.
- Now AU which is the angular bisector of ∠TAB, AU is joined. Now, ∠UAB = \(22 \frac{1}{2}^{\circ}\)
(iii) To construct an angle of 15° :
Solution:
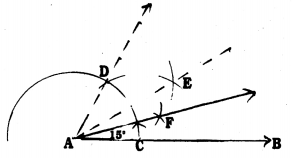
Steps of Construction :
- Draw a straight line AB.
- With A as centre with a convenient radius draw an arc which intersect AB at C.
- With C as centre, with the same radius, draw an arc which intersects at D.
Now. ∠DAB = 60° - Construct AE, the bisector of ∠DAB. Join then, ∠EAB = 30°.
- Construct AF, the bisector of ∠EAB. Join then, ∠FAB = 15°.
Question 4.
Construct the following angles and verify by measuring them by a protractor :
(i) 75°
(ii) 105°
(iii) 135°.
Solution:
(i) To construct angle 75° :
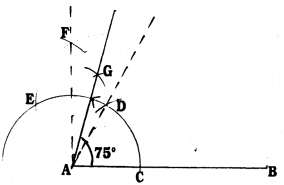
Steps of Construction :
- Draw AB with any measurement.
- With A as centre, with convenient scale draw an arc AB which intersects at C.
- With C as centre with the same radius draw an arc which intersects at D. ∠DAB = 60°.
- With D as centre with the same radius draw an arc which intersects at E.
- With Centres E and D, by taking more than half of ED draw two arcs which meet at E. AF is joined.
Now, ∠FAB = 90°. - Draw AG bisector of ∠EAD, AG joined. ∠GAD = 15°.
- ∠GAD + ∠DAB = 15 + 60 = 75°
∴ ∠GAB = 75°.
(ii) To construct angle 105° :
Solution:
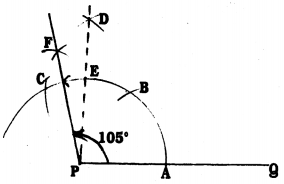
Steps of Construction :
- Draw PQ with any measurement.
- With P as centre and with any radius, draw an arc which intersects PQ at A.
- With A as centre, with the same radius draw an arc which intersect at B.
- With B as centre with same radius draw another arc, it intersects at C.
- With centres C and B if two arcs are drawn these two meet at D. Join PD. ∠DPQ = 90°. Straight-line PD intersects the arc CB at E.
- Now taking radius half of CE, if the line is drawn from C to E it intersects at F. FP is joined. Now ∠FPD = 15°.
- ∠FPD + ∠DPQ = 15 + 90 = 105°.
∴ ∠FPQ = 105° is constructed.
(iii) To construct an angle of 135°
Solution:
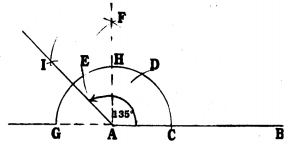
Steps of Construction :
- Draw a straight line AB.
- With A as centre, a semicircle is drawn which meets AB at C and it intersects the produced BA line at G.
- With C as centre with the same radius and centre CD, draw a radius of arc DE.
- With centres E and D by taking a radius more than half draw two arcs which meet at F. Join AF. ∠FAB = 90°. AF intersects ED at H.
- With G and H centres by taking radius more than \(\frac{1}{2}\) of the radius GH draw arcs which meet at I. AI is joined. Now, ∠IAF = 45°.
- ∠IAF + ∠FAB = 45° + 90° = 135°
∴ ∠IAB = 135° is constructed.
Question 5.
Construct an equilateral triangle, given its side, and justify the construction.
Solution:
Data: Construct an equilateral triangle, given its side.
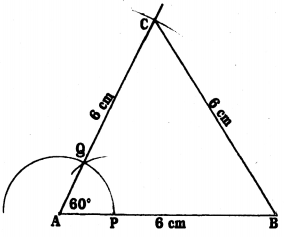
Steps of Construction :
- Construct AB = 6 cm.
- With A as centre and convenient scale draw an arc, it meets AB at P.
- With P as centre, with same radius draw an arc, it intersects the first arc at Q, AQ is joined and produced. ∠QAB = 60°.
- With A as centre and taking 6 cm radius draw an arc. It intersects at C which is the produced line of AQ.
- Next, BC is joined, ABC is an equilateral triangle.
In ∆ABC, ∠A = ∠B = ∠C = 60°
AB = BC = CA = 6 cm.
In ∆ABC, AB = AC = 6 cm. ∠A = 60°
∠B = 60°
∠A + ∠B + ∠C = 180°
60 + ∠B + ∠B =180 (∵ ∠B = ∠C)
60 + 2∠B = 180
2∠B = 180 – 60
2∠B = 120°
∴ ∠B = \(\frac{120}{2}\)
∴ ∠B = 60°
∴∠B = ∠C = 60°
∴∠A = ∠B = ∠C = 60°
AC = BC (Opposite sides of equal angles)
But, AB = AC (known)
∴ AB = BC = CA = 6 cm.
We hope the KSEEB Solutions for Class 9 Maths Chapter 6 Constructions Ex 6.1 help you. If you have any query regarding Karnataka Board Class 9 Maths Chapter 6 Constructions Exercise 6.1, drop a comment below and we will get back to you at the earliest.