KSEEB Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Additional Questions

Students can Download Class 10 Maths Chapter 7 Coordinate Geometry Additional Questions, Notes Pdf, KSEEB Solutions for Class 10 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka State Syllabus Class 10 Maths Chapter 7 Coordinate Geometry Additional Questions

I. Multiple-choice Questions:

Question 1.
The co-ordinates of origin are
a. 0,0.
b. 0, 1.
c. 1, 0.
d. 1, 1.
Answer:
a. 0,0.

Question 2.
The distance of the point (3, 4) x – co-ordinate is equal to
a. 3
b. 4
c. 1
d. 7
Answer:
b. 4

Question 3.
The distance of the point (3, 4) from y-axis is
a. 3
b. 4
c. 5
d. 1
Answer:
a. 3

Question 4.
The angle between x-axis and y-axis is
a. 0°
b. 45°
c. 60°
d. 90°
Answer:
d. 90°

Question 5.
The distance of the point (α, β) from origin is
a. α.β
b. α². β²
c. \(\sqrt{\alpha^{2}-\beta^{2}}\)
d. \(\sqrt{\alpha^{2}+\beta^{2}}\)
Answer:
d. \(\sqrt{\alpha^{2}+\beta^{2}}\)

Question 6.
The distance between the point (x₁,y₁) and (x₂, y₂) is

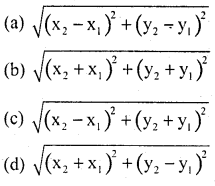
Answer:

Question 7.
Which of the following is distance formula?
Answer:
a. The distance between 2 points (x₁,y₁) and (x₂, y₂) is

b. The mid point of the lines segment join the points (x, y) and (x₂, y₂)

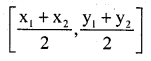
c. The co-ordinates of the centroid of the ∆^le ABC where A, B, C are (x₁,y₁)

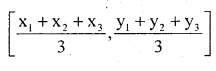
d.

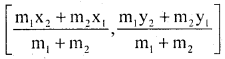
Question 8.
The distance b/w the point (0, 3) and (- 2, 0) is
a. \(\sqrt{14}\)
b. \(\sqrt{15}\)
c. \(\sqrt{13}\)
d. \(\sqrt{5}\)
Answer:
c. \(\sqrt{13}\)

Question 9.
The ∆^le with vertices (- 2, 1) (2, – 2) and (5, 2) is
a. Scalene
b. Equilateral
c. Isosceles
d. right angled isosceles
Answer:
d. right angled isosceles

Question 10.
The Co-ordinates of the point which divides the join of (x, y) and (x₂, y₂) in the ratio m₁ : m₂ internally are

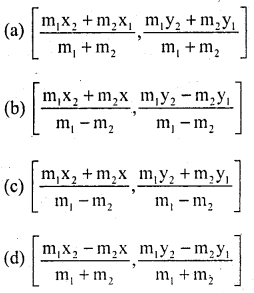
Answer:

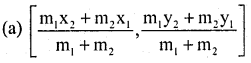
Question 11.
If the distance b/w the point (3, a) and (4,1) is \(\sqrt{10}\), then, find the values of a
a. 3,- 1
b. 4, – 2
c. 2, – 2
d. 5, – 3
Answer:
c. 2, – 2

Question 12.
The distance of the mid – point of the line -segment joining the points 6, 8. and 2, 4. from the point (1, 2) is
a. 3
b. 4
c. 5
d. 6
Answer:
c. 5

Question 13.
The coordinates of the mid – point of the line – segment joining (- 8, 13) and (x, – 7)
a. 16
b. 10
c. 4
d. 8
Answer:
a. 16

Question 14.
Find the value of k if the distance b/w (k, 3) and (2, 3) is 5
a. 5
b. 6
c. 7
d. 8
Answer:
c. 7

Question 15.
The distance b/w the point (Sin θ, Sin θ) & (cos θ, – cos θ) is
a. \(\sqrt{2}\)
b. 2
c. \(\sqrt{3}\)
d. 1
Answer:
a. \(\sqrt{2}\)

II. Short Answers Questions:

Question 1.
Write the coordinate of the origin.
Answer:
(0, 0)

Question 2.
What is the ordinate of all the point on x-axis
Answer:
0(zero)

Question 3.
Find the perpendicular distance of the point (- 3, 5) form the x – axis.
Answer:
5

Question 4.
Find the distance of B(3 + \(\sqrt{3}\), 3 – \(\sqrt{3}\)) form origin.
Answer:

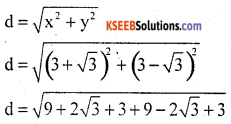
d = \(\sqrt{24}\)
d = \(\sqrt{4 \times 6}\)
d = 2\(\sqrt{6}\)

Question 5.
Write the formula to find distance b/w two points
Answer:

Question 6.
Write the formula to find distance b/W point and origin.
Answer:
d = \(\sqrt{x^{2}+y^{2}}\)

Question 7.
Write the formula to find area of triangle.
Answer:
area of triangle

Question 8.
Find the value of a, so that the point (3, a) lie on the line 2x – 3y = 5.
Answer:
Since (3, a) lies on the line 2x – 3y = 5
Then 2(3) – 3(a) = 5
6 – 3a = 5
– 3a = 5 – 6
– 3a = – 1
a = 1/3

Question 9.
Write the section formula when it divide in ration p : q
Answer:
Co-ordinates

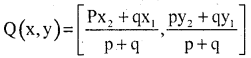
III. Long Answer Questions:

Question 1.
Find the distance between the following pairs of points.
i) (6, 5) and (4, 4)
Answer:

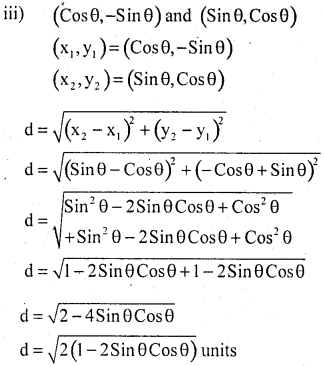
Question 2.
The distance between the point (3, 1) and (0, x) in 5 unit. Find x.
Answer:
(x₁, y₁) = (3, 1); (x₂, y₂) = (o, x)
d = 5

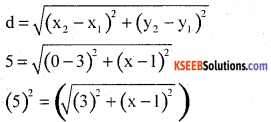
(∵ squaring on both the sides)
25 = (3)₂ + (x – 1)₂
x₂ + 1 – 2x + 9 = 25
x₂ + 1 – 2x + 9 – 25 = 0
x₂ + 1 – 2x + 9 – 25 = 0
x₂ – 2x – 15 = 0
x₂ – 5x + 3x – 15 = 0
x(x – 5) + 3(x – 5) = 0
(x – 5)(x + 3) = 0
x – 5 = 0, x + 3 = 0
x = 5, x = – 3

Question 3.
Find a point on y-axis which is equidistant from the points (5, 2) and (- 4, 3)
Answer:
A Point lie on y – axis = (0, y) the points are equidistant from the point on y – axis.

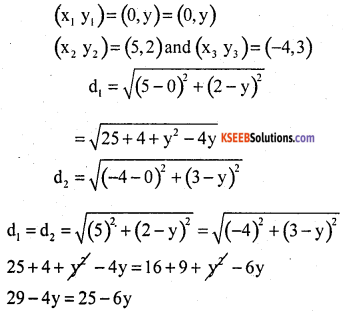
6y – 4y = 25 – 29
2y = – 4
y = \(\frac{-4}{2}\) ⇒ y = – 2
∴ point on y – axis is y = – 2

Question 4.
Find the radius of a circle whose centre is (- 5, 4) and which passes through the point (- 7,1)

Question 5.
Prove that each of the set of co¬ordinates are the vertices of parallelograms.
i. (- 5, – 3), (1, – 11), (7, – 6), (1, 2).
Answer:


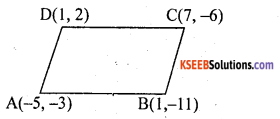
∴ AD = BC & AB = CD
∴ Given vertices from a parallelogram.

Question 6.
In what ratio does the point (- 2, 3) divide the line segment joining the point (- 3, 5) and (4, – a)?
Answer:
(x₁, y₁) = (3, 5)
(x₂, y₂) = (4, – a)
p(x, y) = (- 2, 3)


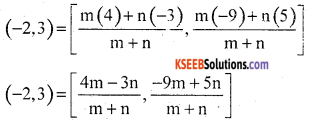
4m – 3n = – 2(m + n)
4m – 3n = – 2m – 2n
4m + 2m = – 2n + 3n
6m = n
\(\frac{m}{n}=\frac{1}{6}\)
m : n = 1 : 6 (or)
\(\frac{-9 m+5 n}{m+n}\) = 3
– 9m + 5n = 3(m + n)
– 9m + 5n = 3m + 3n
– 9m – 3m = 3n – 5n
– 12m = – 2n
\(\frac{m}{n}=\frac{-2}{-12}=\frac{1}{6}\)
m : n = 1 : 6

Question 7.
In the point C(1, 1) divides the line segment joining A(- 2, 7) and B in the ration 3 : 2 find the co-ordinates of B.
Answer:
Point C(1, 1)
(x₁, y₁) = A(- 2, 7) m : n = 3 : 2
B(x₂, y₂) =?


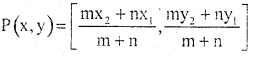
∴ Co-ordinate of B = (3, – 3)

Question 8.
Find the ratio in which the point (- 1, k) divides the line joining the points (- 3, 10) and (6, – 8) and also find ‘k’.
Answer:
P(x, y) = (- 1, k); (x₁, y₁) = (- 3,10)
(x₂, y₂) = (6,- 8)

6m – 3n = – (m + n)
6m – 3n = – m – n
6m + m = 3n – n, \(\frac{-8 m+10 n}{m+n}\) = k

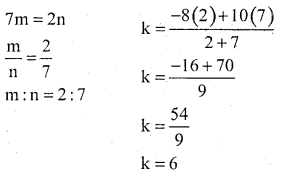
Question 9.
Three Consecutive vertices of a parallelogram are A(1, 2), B(2, 3) and (8, 5). Find the fourth vertex.
Answer:

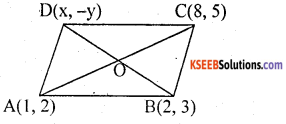
‘O’ is the mid point of AC and by using mid point formulas AC is a line and ‘O’ is the point
A(x₁, y₁) =(1, 2);
c(x₂, y₂) = (8, 5)
Co-ordinates of

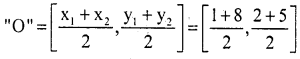
Co-ordinates of ‘O’ = \(\frac{9}{2}, \frac{7}{2}\)
BD is a line and ‘O’ is midpoint
B(2, 3) = (x₁, y₁); D(x, y) = (x₂, y₂)
\(\left(\frac{9}{2} \frac{7}{2}\right)\) = (x, y)
By midpoint formula
Co-ordinates of

2 + x = 9 3 + y = 7
x = 9 – 2 y = 7 – 3
x = 7 y = 4
the fourth vertex is (7, 4)

Question 10.
Find the relation between x and y, if the points (x, y) (1, 2) and (7, 0) are colliner.
Answer:
Given point are A(x, y), B(1, 2) and C(7, 0)
These points will be collinear if the area of the triangle formed by them is zero.
Now, ar(ABC)

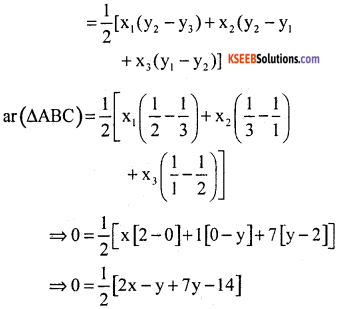
⇒ 2x + 6y – 14 = 0
⇒ x + 3y = 7
which is the required relation between x & y

Question 11.
Find the ratio in which the line segment joining the points A(3, – 3) and B(- 2,7) is divides by x-axis. Also find the Co-ordinates of the point of division.
Answer:

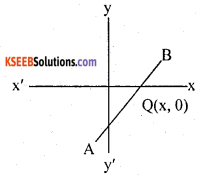
Here, point Q is an x-axis its ordinate & 0
Let ratio be k : 1 and Co-ordinate of point Q be (x, 0)

Question 12.
If A(4, 2), B = (7, 6) and C(1, 4) are the vertices of ∆ ABC and AD is its median, P.T that median AD divides ∆ ABC into two triangle of equal areas.D is the median on BC
⇒ The Co-ordinates of midpoint D are given by

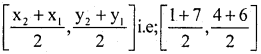
Co-ordinates of D are (4, 5)
Now, Area of triangle
ABD = \(\frac{1}{2}\)[x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)
= \(\frac{1}{2}\)[4(6 – 5) + 7(52) + 4(2 – 6)
= \(\frac{1}{2}\)[4 + 21 – 16] = \(\frac{1}{2}\) sq.units
Area of
∆ ACD = \(\frac{1}{2}\)[4[4 – 5] + 1[5 – 2] + 4[2 – 4]]
= \(\frac{1}{2}\)[- 4 + 3 – 8] = \(\frac{-9}{2}=\frac{9}{2}\) sq.units

Question 13.
In what ratio does the y – axis divide the line segment joining the point p(- 4, 5) and Q(3, 7). Also, find the co-ordinates of the intersection.
Answer:

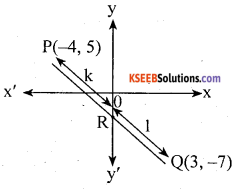
Suppose y – axis divides PQ in the ratio k : 1. Then the co-ordinates of the point of division are

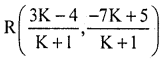
Since, R lies on y-axis and X Co-ordinate of every point on y-axis is zero.
∴ \(\frac{3 \mathrm{K}-4}{\mathrm{K}+1}\) = 0
⇒ 3k – 4 = 0 ⇒ K = \(\frac{4}{3}\)
Hence, the required ratio is 4/3 : 1 i.e, 4 : 3
Putting K = 4/3 in the Co-ordinates of R, we find that its Co-ordinates are (0, – 13/7)

Question 14.
Show that ∆ ABC with vertices A(- 2, 0), B(2, 0) and C(0, 2) is similar to ∆ DEF with vertices D(- 4, 0), E(4, 0) and F(0, 4)
Answer:
Given vertices of ∆ ABC and ∆ DEF are

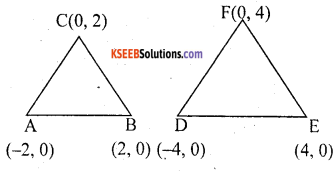
A(- 2, 0), B(2, 0), C(0, 2), D(- 4, 0), E(4, 0) and F(0, 4)

Here, we see that sides of ∆ DEF are twice the sides of a ∆ ABC.
Hence, both triangle are similar.