Students can Download Chapter 4 Simple Equations Ex 4.3, Question and Answers, Notes Pdf, KSEEB Solutions for Class 7 Maths, Karnataka State Board Solutions help you to revise complete Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 7 Maths Chapter 4 Simple Equations Ex 4.3
Question 1.
Solve the following equations :
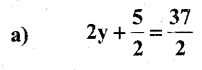
Solution:

Substitute the value of y = 8 in the given equation

∴ LHS = RHS (verified)
b) 5t + 28 = 10
Solution:
The given equation is 5t + 28 = 10
Transposing 28 from LHS to RHS
5t = 10 – 28 [on transposing + 28 becomes -28]
5t = -18
Dividing by 5 both the sides
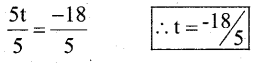
Substitute the value of t = \(\frac{-18}{5}\) in the given equation
5t + 28 = 10
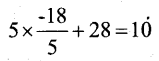
-18 + 28 = 10
10 = 10
∴ LHS = RHS (verified)
c)
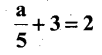
Solution:
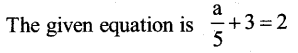
Transposing + 3 from LHS to RHS

Multiply by 5 both the sides
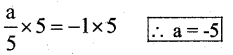
Substitute the value of a = -5 in the given equation.

-1 + 3 = 2
2 = 2
∴ LHS = RHS (verified)
![]()
d)
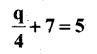
Solution:
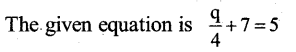
Transposing +7 from LHS to RHS

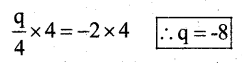
Substitute the value of q = -8 in the given equation.

-2 + 7 = 5
5 = 5
∴ LHS = RHS (verified)
e)

Solution:

Multiply by 2 both the sides
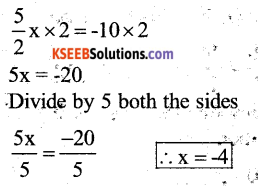
Substitute the value of x = -4 in the given equation.

∴ LHS = RHS (verified)
f)
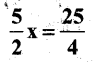
Solution:
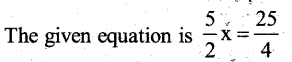
Multiply by 2 both the sides
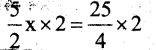

Divide by 5 both the sides
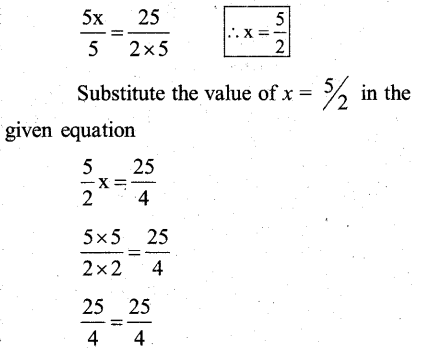
∴ LHS = RHS (verified)
g) 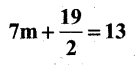
Solution:

Divide by 7 both the sides
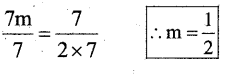
Substitute the value of m = \(\frac{1}{2}\) in the given equation

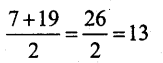
13 = 13
∴ LHS = RHS (verified)
![]()
h) 6z + 10 = -2
Solution:
The given equation is 6z + 10 = -2
Transposing + 10 from LHS to RHS
6z = -2 – 10(on Transposing + 10 becomes – 10)
6z = -12
Divide by 6 both the sides
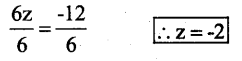
Substitute the value of z = -2 in the given equation
6z + 10 = -2
6(-2) + 10 = -2
-12 + 10 = -2
-2 = -2
∴ LHS = RHS (verified)
i)

Solution:
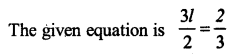
multiply by 2 both the sides

Divide by 3 both the sides
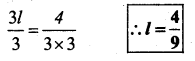
Substitute the value of l = \(4 / 9\) in the given equation.

![]()
∴ LHS = RHS (verified)
j)
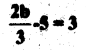
Solution:

Transpose -5 from LHS to RHS

Multiply by 3 both the sides

Divide by 2 both the sides

Substitute the value of b = 12 in the given equation

3 = 3
∴ LHS = RHS (verified)
![]()
Question 2.
Solve the Mowing equations :
a) 2(x+4) = 12
Solution:
The given equation is 2(x + 4) = 12
Divide by 2 both the sides
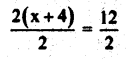
x + 4 = 6
Transpose +4 from LHS to RHS x = 6 – 4 (on transposing 4 becomes -4)
∴ x = 2
Substitute the value of x = 2 in the given equation
2(x + 4) = 12
2(2 + 4) = 12
2(6) = 12
12 = 12
∴ LHS = RHS (verified)
b) 3(n – 5) = 21
The given equation is 3 (n – 5) = 21
Divide by 3 both the sides
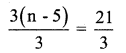
∴ n – 5 = 7
Transpose -5 from LHS to RHS
n = 7 + 5 [on transposing -5 becomes +5]
∴ n = 12
Substitute the value of n = 12 in the given equation
3(n – 5) = 21
3(12 – 5) = 21
3(7) = 21
21 = 21
LHS = RHS (verified)
![]()
c) 3 (n – 5) = -21
The given equation is 3 (n – 5) = -21
Divide by 3 both the sides 3
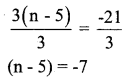
Transpose -5 from LHS to RHS n = -7 + 5 (on transposing -5 becomes +5)
n = -2
Substitute the value n = -2 in the given equation
3 (n – 5) = -21 .
3(-2 – 5) = -21
3(-7) = -21
-21 = -21
∴ LHS = RHS (verified)
d) -4(2 + x) = 8
Solution:
The given equation is -4 (2 + x) = 8
Divide by -4 both the sides
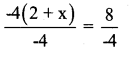
2 + x = -2
Transpose 2 from LHS to RHS x = -2 -2 [on transposing 2 becomes -2]
∴ x = -4
Substitute the value of x = -4 in the given equation
-4(2 + x) = 8
-4(2 – 4) = 8
-4 (-2) = 8
8 = 8
∴ LHS = RHS (verified)
e) 4 (2 – x) = 8
The given equation is 4 (2 – x) = 8
Divide by 4 both the sides

2 – x = 2
Transpose +2 from LHS to RHS
-x = 2 – 2 (on transposing 2 becomes -2)
-x = 0
multiply by -1 both the sides
-x × -1 = 0 × -1 x = 0
Substituting the value of x = 0 in the given equation
4(2 – x) = 8
4(2 – 0) = 8
8 – 0 = 8
8 = 8
∴ LHS = RHS (verified)
![]()
Question 3.
Solve the following equations :
a) 4 = 5 (p – 2)
Solution:
The given equation is 4 = 5 (p – 2)
5(p – 2) = 4 [LHS and RHS are inter-changed the equation remains the same]
Divide by 5 both sides

![]()
Transpose -2 from LHS to RHS

Substituting the value of p = \(\frac{14}{5}\) in the given equation

∴ LHS = RHS (verified)
b) -4 = 5 (p – 2)
Solution:
The given equation is – 4 = 5 (p – 2)
[LHS & RHS are interchanged the equation remains same]
5 (p – 2) = -4
Divide by 5 both the sides

Transpose -2 from LHS to RHS
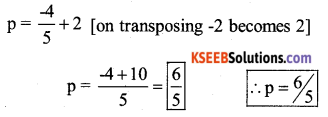
Substitute the value of P = 6/5 in the given equation
5(p – 2) = -4
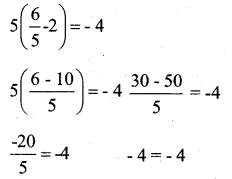
∴ LHS = RHS (verified)
c) 16 = 4 + 3 (t + 2)
Solution:
The given equation is 16 = 4 + 3 (t + 2)
4 + 3 (t + 2) = 16 [LHS and RHS are interchanged the equation remains the same.] 4 + 3t + 6 = 16
3t + 10 = 16
3t = 16 – 10 [ transposing + 10 from LHS to RHS, it becomes -10]
3t = 6
t = 6/3 = 2 ∴ t = 2
Substitute the value of t = 2 in the given equation
16 = 4 + 3 (t +2)
16 = 4 + 3t + 6
16 = 10 + 3(2)
16 = 10 + 6
16 = 16
∴ LHS = RHS (verified)
d) 4 + 5 (p – 1) = 34
Solution:
The given equation is 4 + 5 (p – 1) = 34
Transpose 4 from LHS to RHS
5(p – 1) = 34 – 4 (on transposing 4 becomes -4)
5(p – 1) = 30
Divide by 5 both sides

p – 1 = 6
Transposing -1 from LHS to RHS p = 6 + 1 [on transposing -1 becomes 1]
p = 7
Substitute the value of p = 7 in the given equation
4 + 5(p – 1) = 34
4 + 5p – 5 = 34
4 + 5 (7) – 5 = 34
4 + 35 – 5 = 34
34 = 34
∴ LHS = RHS (verified)
![]()
e) 0 = 16 + 4(m – 6)
Solution:
The given equation is 0 = 16 + 4 (m – 6)
16 + 4 (m – 6) = 0 [ LHS ami RHS are interchanged the equation remains the same] Transpose 16 from LHS to RHS .
4(m – 6) = 0 – 16 [on transposing 16 becomes -16]
4(m – 6) = -16
Divide by 4 both sides
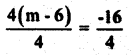
m – 6 = – 4
Transpose – 6 from LHS to RHS
m = – 4 + 6 [on transposing – 6 becomes + 6]
m = 2
Substitute the value m = 2 in the given equation
16 + 4(m – 6) = 0
16 + 4(2 – 6) = 0
16 + 4(-4) = 0
16 – 16 = 0
0 = 0
∴ LHS = RHS (verified)
Question 4.
a) Construct 3 equations starting with x = 2
Solution:
x = 2
multiply by 3 both sides
3(x) = 2(3)
3x = 6
Add 6 to both sides
3x + 6 = 6 + 6
equation 1 3x + 6 = 12
x = 2
multiply by 12 both sides
12(x) = 2(12)
12x = 24
Subtract 10 from both sides
12x – 10 = 24 – 10
equation 2 12x – 10 = 14
multiply by 15 both the sides
x (15) = 2(15)
15x = 30
Divide by 2 both the sides
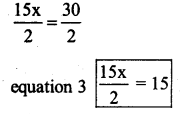
![]()
b) Construct 3 equations starting with x = -2
Solution:
x = -2
multiply by 5 both sides
5(x) = -2 (5)
5x = -10
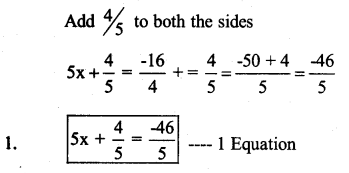
x = -2
multiply by 8 both the sides
8(x) = -2 × 8
8x = -16
Divide by 3 both the sides
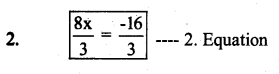
x = -2
multiply by 9 both the sides
9(x) = -2 × 9
9x = -18
Subtract 7 from both the sides 9x-l – -18 – 7
3. 9x – 7 = -25 —– 3. Equation