Students can Download Maths Chapter 7 Rational Numbers Additional Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 8 Maths Chapter 7 Rational Numbers Additional Questions
I. Fill in the blanks:
Question 1.
(a) The number 0 is not in the set of Natural numbers
(b) The least number in the set of all whole numbers is O
(c) The least number in the set of al even natural numbers is 2
(d) The successor of 8 in the set of all-natural numbers is 9
(e) The sum of two odd integers is even
(f) The product of two odd integers is odd
![]()
Question 2.
State whether the following statements are true or false.
(a) The set of all even natural numbers is a finite set.
Answer:
False.
(b) Every non-empty subset of Z has the smallest element.
Answer:
False
(c) Every integer can be identified with a rational number
Answer:
True
(d) For each rational number, one can find the ne×t rational number
Answer:
False
(e) There is the largest rational number
Answer:
False
(f) Every integer is either even or odd
Answer:
True
(g) Between any two rational numbers, there is an integer.
Answer:
False
![]()
Question 3.
Simplify:
(i) 100(100 – 3) – (100 × 100 – 3)
Solution:
100(97) – (10000 – 3)
= 9700 – (9997) = – 297
(ii) (20 – (2011 – 201) + 2011 – (201 – 20))
= 20 – 2011 + 201 + 2011 – 201 + 20 = 40
Question 4.
Suppose m is an integer such that m * -1 and m ≠ – 2. Which is larger \(\frac{m}{m+1} \text { or } \frac{m+1}{m+2} ?\) State your reasons.
Solution:

![]()
Question 5.
Define as operation * on the set of all rational numbers Q as follows r * s = r + s – (r × s) for any two rational numbers r, s. Answer the following with justification.
(i) Is Q closed under the operatiron ?
(ii) Is * an associative operation on Q?
(iii) Is * commutative operation on Q?
(iv) What is a * 1 for any a in Q?
(v) Find two integers a ≠ 0, b ≠ 0 such that a * b = 0
Solution:

Q is closed under the operation *. because ∀r, s ∈ Q r * s = r + s – (r × s) is also a rational number.
(ii) Let r, s and p ∈ Q
r * (s * p) = r * (s + p – (s × p))
= r + s + p – (s × p) – (r × (s + p – (s × p)
= r + s + p – sp – (rs + rp – rsp)
= r + s + p – sp – rs – rp + rsp …(i)
(r * s) * p = r + s – (r × s) * p
= r + s – (r × s) + p – (r + s – (r × s) × p)
= r + s – rs + p – (rp – sp – rsp)
= r + s + p – rs – rp – sp – rsp …(ii)
From (i) and (ii) r * (s * p) = (r * s) * p
∴ * is an associative operation on Q.
(iii) Let r, s, ∈ Q
r * s = r + s – (r × s) = r + s – rs …(i)
s * r = s + r – (s × r) = s + r – sr = r + s – rs …(ii)
From (i) and (ii) r * s = s * r
∴ * is commutative operation on Q.
(vi) r * s = r + s – (r × s)
∴ a * 1 = a + 1 – (a × 1)
= a + 1 – a
a * 1 = 1
(v) r * s = r + s – (r × s)
a * b = a + b – (a × b)
if a = 2, and b = 2
2 * 2 = 2 + 2 – (2 × 2) = 4 – 4
2 * 2 = 0
∴ If a = 2 and b = 2 a * b = 0
![]()
Question 6.
Find the multiplicative inverse of the following rational numbers.
\(\frac{8}{13}\)
Solution:
\(\frac{13}{8}\)
\(\frac{-13}{11}\)
Solution:
\(\frac{-11}{13}\)
\(\frac{12}{17}\)
Solution:
\(\frac{17}{12}\)
\(\frac{-101}{100}\)
Solution:
\(\frac{-100}{101}\)
\(\frac{26}{23}\)
Solution:
\(\frac{23}{26}\)
![]()
Question 7.
Write the following in the increasing order.
\(\frac{10}{13}, \frac{20}{23}, \frac{5}{6}, \frac{40}{43}, \frac{25}{28}, \frac{10}{11}\)
Solution:
Take the LCM of the denominators
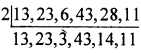
LCM = 2 × 13 × 23 × 3 × 43 × 14 × 11
= 11879868

Question 8.
Write the following in decreasing order
\(\frac{21}{17}, \frac{31}{27}, \frac{13}{11}, \frac{41}{37}, \frac{51}{47}, \frac{9}{8}\)
Solution:
Take the LCM of the denominators
LCM = 17 × 27 × 11 × 37 × 47 × 8 = 70241688

Question 9.
(a) What is the additive inverse of O?
Solution:
O
(b) What is the multiplicative inverse of 1?
Solution:
1
(c) Which integers have a multiplicative inverse?
Solution:
1 and -1
![]()
Question 10.
In the set of all rational numbers, give 2 examples each illustrating the following properties.
(i) Associativity
(a)
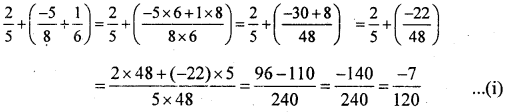
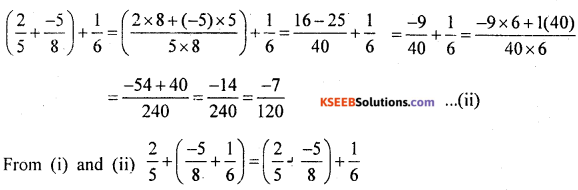
Associative property of addition in satisfied.
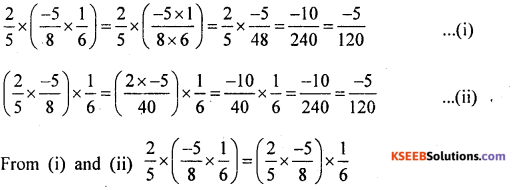
Associative property of multiplication is satisfied.
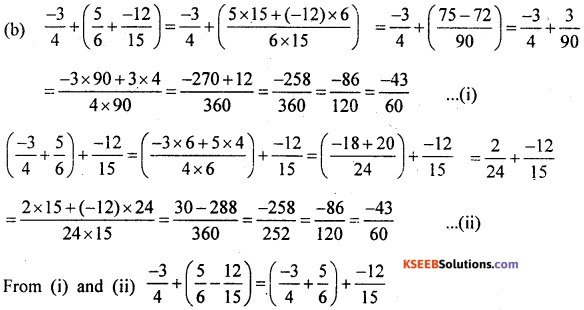
Associative property of addition is satisfied.
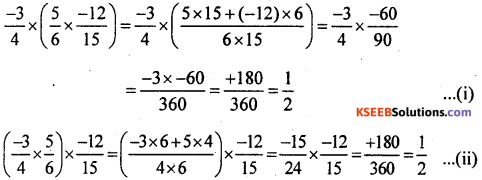
From (i) and (ii)

Associative property of multiplication is satisfied.
(ii) Commutativity
(a)
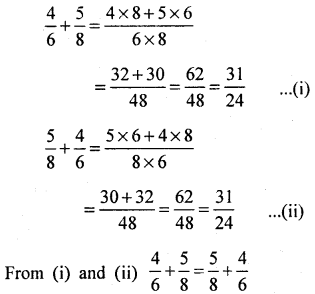
Comutative property of addition is satis¬fied.
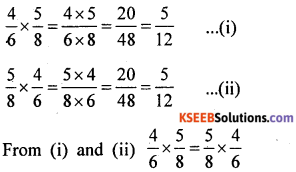
Commutative property of multiplication is satisfied
(b)
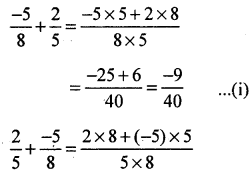
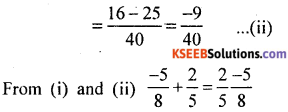
Commutative property of addition is satisfied.
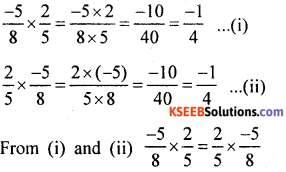
Commutative property of multiplication is satisfied.
(iii) Distributivity of multiplication over addition.
(a)
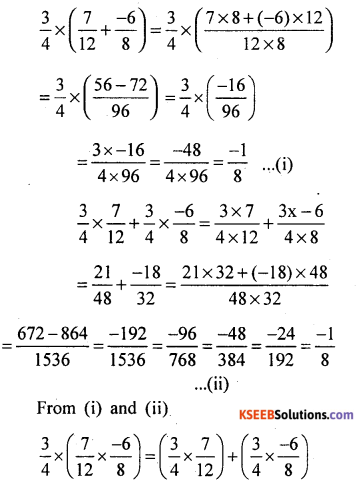
Multiplication is distributive over addition.
(b)
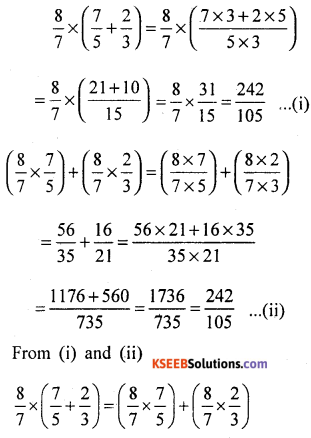
∴ Multiplication is distributive over addition.
![]()
Question 11.
Simplify the following using distributive property
(1) \(\frac{2}{5} \times\left(\frac{1}{9}+\frac{2}{5}\right)\)
Solution:
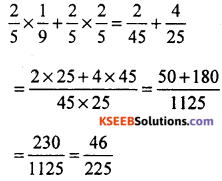
(2) \(\frac{5}{12} \times\left(\frac{25}{9}+\frac{32}{5}\right)\)
Solution:
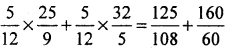

(3) \(\frac{8}{9} \times\left(\frac{11}{2}+\frac{2}{9}\right)\)
Solution:

Question 12.
Simplify the following:
(i) \(\left(\frac{25}{9}+\frac{12}{3}\right)+\frac{3}{5}\)
Solution:
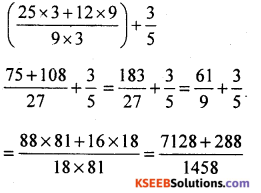
(ii) \(\left(\frac{22}{7}+\frac{36}{5}\right) \times \frac{6}{7}\)
Solution:
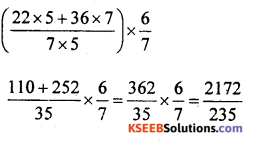
(iii) \(\left(\frac{51}{2}+\frac{7}{6}\right) \div \frac{3}{5}\)
Solution:

(iv) \(\left(\frac{16}{7}+\frac{21}{8}\right) \times\left(\frac{15}{3}-\frac{2}{9}\right)\)
Solution:
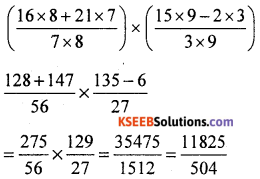
Question 13.
Which is the property that is there in the set of all rational numbers but which is not in the set of all integers?
Solution:
Every non zero rational number is invertible but only + 1 are invertible integers.
Question 14.
What is the value of \(1+\frac{1}{1+\frac{1}{1+1}}\)
Solution:
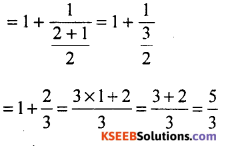
Question 15.
Find the value of \(\left(\frac{1}{3}-\frac{1}{4}\right) /\left(\frac{1}{2}-\frac{1}{3}\right)\)
Solution:
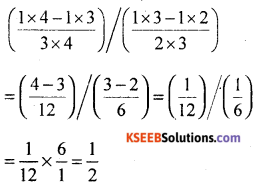
![]()
Question 16.
Find all rational numbers each of which is equl to its reciprocal.
Solution:
The rational numbers + 1 and – 1 and their reciprocals are equal.
Question 17.
A bus shuttles between two neighbouring towns every two hours. It starts from 8 AM in the morning and the last trip in at 6 PM. On one day the driver observed that the first trip had 30 passengers and each subsequent trip had one passenger less than the previous trip. How many passengers travelled on that day?
Solution:
The number of trips = 6 The number of passengers in the first rip is 30, second trip in 29, third trip is 28 and so on
∴ No of passenger travelled on that day = 30 + 29 + 28 + 27 + 26 + 25 = 165
Question 18.
How many rational numbers p/q are there between 0 and 1 for which q < P?
Solution:
There are no rational numbers between 0 and 1 such that q < p.
Question 19.
Find all integers such that \(\frac{3 n+4}{n+2}\) is also an integer.
Solution:
Let n = 0
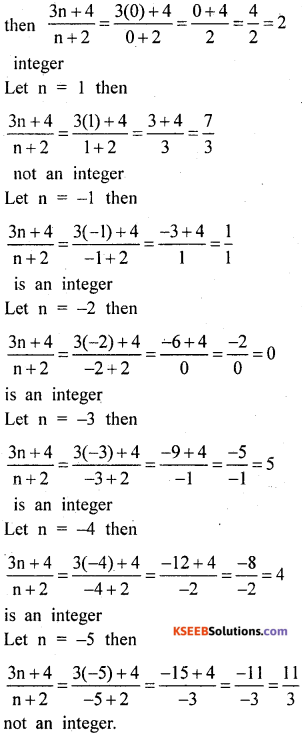
It is an integer if n = 0, – 1, – 2, – 3, – 4.
Question 20.
By inserting parenthesis (that is brackets), you can get several values for 2 × 3 + 4 × 5 (For example ((2 × 3) + 4) × 5 is one way of inserting parenthesis) How many such values are there?
Solution:
(i) (2 × 3) + (4 × 5) = 6 + 20 = 26
(ii) 2 × (3 + 4) × 5 = 2 × 7 × 5 = 70
(iii) 2 × (3 + (4 × 5)) – 2 × (3 + 20) = 2 × 23 = 46
(iv) ((2 × 3) + 4) × 5 = (6 + 4) × 5 = 10 × 5 = 50 There are 4 values
![]()
Question 21.
Suppose \(\frac{p}{q}\) is a positive rational in its lowest form prove that \(\frac{1}{q}+\frac{1}{p+q}\) is also in its lowest form.
Solution:
\(\frac{p}{q}\) is in its lowest form means p and q do not have any common factors other than 1.
Consider \(\frac{1}{q}+\frac{1}{p+q}=\frac{p+q+q}{q(p+q)}=\frac{p+2 q}{q(p+q)}\) p + 2q and q (p + q) do not have common factors other than 1 ∴ \(\frac{p+2 q}{q(p+q)}\) is in its lowest form, that means \(\frac{1}{q}+\frac{1}{p+q}\) is in its lowest form.
Question 22.
Show that for each natural number n the fraction \(\frac{14 n+3}{21 n+4}\) is in its lowest form
Solution:
If
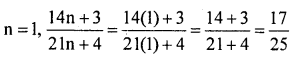
is in the lowest form
If
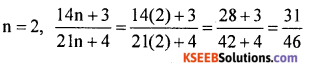
is in the lowest form
If
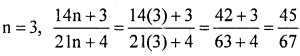
is in the lowest form
If
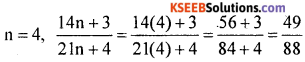
is in the lowest form.
Similarly by substituting natural numbers
for n we can show that \(\frac{14 n+3}{21 n+4}\) is in its lowest form.
Question 23.
Find all integers n for which the number (n + 3) (n – 1) is also an integer.
Sol:
If n = 0, (n + 3) (n – 1) = (0 + 3) (0 – 1) = 3x-l = -3 is an integer If n = 1, (n + 3) (n – 1) = (1 + 3) (1 – 1) = 4×0 = 0 is an integer.
If n = – 1, (n + 3) (n – 1) = (- 1 + 3) (- 1 – 1) = 3 (- 2) = – 6 is an integer Similarly when n is replaced by any integer we find that (n + 3) (n – 1) is also an integer
∴ n = { ……….. – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4 ……….}
![]()