KSEEB SSLC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Ex 7.1 are part of KSEEB SSLC Class 10 Maths Solutions. Here we have given Karnataka SSLC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.1.
Karnataka SSLC Class 10 Maths Solutions Chapter 7 Coordinate Geometry Exercise 7.1
Question 1.
Find the distance between the following pairs of points:
i) (2, 3), (4, 1)
ii) (-5, 7), (-1, 3)
iii) (a, b), (-a,-b)
Solution:
i) If A(x1, y1) = A(2, 3)
B(x2, y2) = B(4, 1), then
ii) Let P(x1, y1) = P(-5, 7)
Q(x2, y2) = Q(-1, 3)
iii) A (a, b), B (-a, -b)
Question 2.
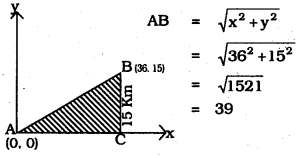
Find the distance between the points (0, 0) and (36, 15). can you now find the distance between the two towns A and B discussed in Section 7.2?
Solution:
The distance between the points A(0, 0) and B(36, 15):
∴ AB = 39
∴ The distance between the two towns A and B discussed in section 7.2 is
Question 3.
Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Solution:
Whether the points A (1, 5), B (2, 3) and C (-2, -11) are collinear?
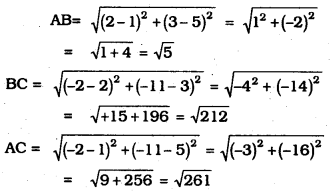
Here, AB + BC = AC, then it is straight line.
But \(\sqrt{5}+\sqrt{221} \neq \sqrt{261}\)
∴ These points are non-collinear.
Question 4.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Solution:
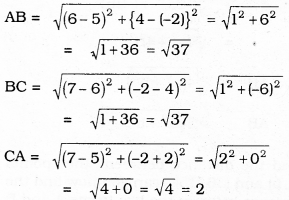
Here, AB = BC.
∴ If Two sides of the triangle ABC are equal to each other then it is an isosceles triangle.
Question 5.
In a classroom, 4 friends are seated at the points, A, B, C, and D as shown in the following figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using the distance formula, find which of them is correct.
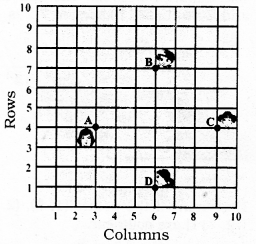
Solution:
A(3, 4), B (6, 7), C (9, 4), D (6, 1)
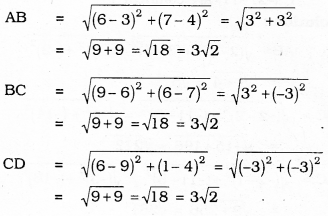
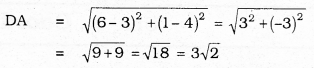
Four sides of quadrilateral ABCD are equal to each other.
∵ AB = BC = CD = DA = \(3 \sqrt{2}\)
Diagonal AC = Diagonal BD
∴ ABCD is a square.
∴ Champa is correct among the two.
Question 6.
Name the type of quadrilateral formed, if any, by the following points, and give reasons 1 for your answer :
i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
iii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution:
i) A (1, -2), B (1, 0), C (-1, 2), D (-3, 0)
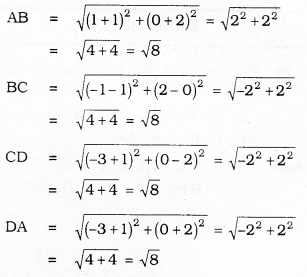
In the quadrilateral ABCD,
diagonal AC = diagonal BD = 4 cm., and
AB = BC = CD = DA = \(\sqrt{8}\) units.
i. e., Here all four sides are equal to each other then ABCD is a square.
ii) P (-3, 5), Q (3, 1), R (0, 3), S (-1, -4)
As per Distance formula,

Here all four sides of quadrilateral PQRS are not equal to each other. Hence PQRS is a quadrilateral.
iii) A (4, 5), B (7, 6), C (4, 3), D (1, 2)
As per the Distance formula,

In the quadrilateral ABCD
AB = DC = \(\sqrt{10}\)
BC = AD = \(\sqrt{18}\)
Diagonal AC ≠ Diagonal BD
Adjacent sides are equal to each other and diagonals are not equal to each other. This is a parallelogram.
Question 7.
Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).
![]()
Solution:
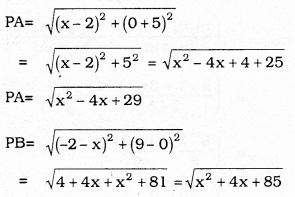
we have PA = PB
∴ PA2 = PB2
x2 – 4x + 29 = x2 + 4x + 85
-4x – 4x = 85 – 29
-8x = 56
8x = -56
∴ x = \(\frac{-56}{8}\)
∴ x = – 7
∴ Coordinates of P are (x, 0), it means (-7, 0).
∴ Required point (x, 0) = (-7, 0)
∴ x = -7.
Question 8.
Find the values of ‘y’ for which the distance between the points P(2, -3) and Q (10, y) is 10 units.
Solution:
If the distance between P and Q, PQ = 10 units, then y =?
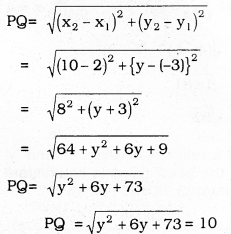
By Squaring on both sides,
y2 + 6y + 73 = 100
y2 + 6y + 73 – 100 = 0
y2 + 6y – 27 = 0
y2 + 9y – 3y – 27 = 0
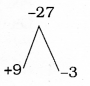
y (y + 9) – 3(y + 9) = 0
(y + 9) (y – 3) = 0
If y + 9 = 0 then OR y – 3 = 0 then
y = -9 y = 0
∴ y = -9 OR +3.
Question 9.
If Q (0, 1) is equidistant from P (5, -3) and R(x, 6), find the value of x. Also, find the distances QR and PR.
![]()
Solution:
Point Q is equidistant from P and R, then PQ = QR, x = ?
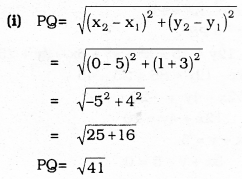
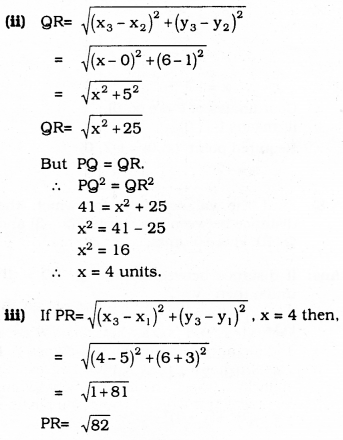
Question 10.
Find a relation between ‘x’ and ‘y’ such that the point (x, y) is equidistant from the point (3, 6) and (-3, 4).
![]()
Solution:
A (3, 6) = A (x1, y1) AP = PB.
P(x, y)
Let B(-3, 4) = B(x2, y2).

Here, AP = PB
∴ AP2 = PB2
x2 – 6x + y2 – 12y + 45 = x2 + y2 + 6x – 8y + 25
-6x – 6x – 12y + 8y = 25 – 45
– 12x – 4y = -20
12x + 4y = 20
∴ 3x + y = 5
∴ 3x + y – 5 = 0
We hope the given KSEEB SSLC Class 10 Maths Solutions Chapter Chapter 7 Coordinate Geometry Ex 7.1 will help you. If you have any query regarding Karnataka SSLC Class 10 Maths Solutions Chapter Chapter 7 Coordinate Geometry Exercise 7.1, drop a comment below and we will get back to you at the earliest