Karnataka Board Class 9 Maths Chapter 12 Circles Ex 12.5
Question 1.
In Fig., A, B, and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
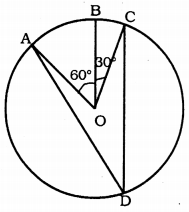
Solution:
∠AOB + ∠BOC = 60° + 30° = 90°
∴ ∠AOC = 90° (Angle subtended at the centre)
∠ADC = ?
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
∴ Angle subtended at the centre
∠AOC= 2 × ∠ADC
90° = 2 × ∠ADC 90
∴ ∠ADC = \(\frac{90}{2}\) = 45°
∴ ∠ADC = 45°.
Question 2.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
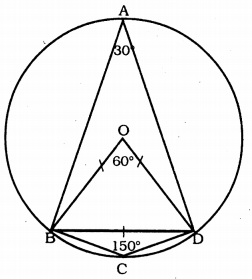
Solution:
(i) Angle subtended in the circumference, ∠BAD =?
(ii) Angle subtended in the circumference, ∠BCD =?
In this figure BD is a chord, OB is the radius, it is equal to OD.
∴ OB = OD = BD
∴ ∆OBD is equilateral triangle.
∴ each angle is equal to 60°.
∴ angle subtended at the centre ∠BOD = 60°.
(i) Angle subtended in the circumference
∠BAD= \(\frac{1}{2}\) × angle subtended at centre ∠BOD
= \(\frac{1}{2}\) × 60°
∴ ∠BAD = 30°.
(ii) The sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
∴ In cyclic quadrilateral ABCD,
∠BAD + ∠ACD = 180
30 + ∠ACD = 180 (∵ ∠BAD = 30°)
∴ ∠ADC = 180 – 30
∴ ∠ACD = 150°.
Question 3.
In Fig., ∠PQR = 100°. where P, Q and R are points on a circle with centre O. Find ∠OPR.
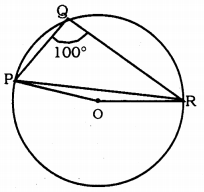
Solution:
If ∠PQR = 100°, then ∠OPR = ?
∠PQR = 100°.
∴ ∠POR = ?
∠POR = 2 × ∠PQR = 2 × 100°
∠POR = 200°
∴ ∠POR – Reflex angle ∠POR = 360°
∴ ∠POR = 360 – 200
∴ ∠POR = 160°
In ∆POR, OP = OR radii.
∴ ∠OPR = ∠ORB
∴ ∠OPR + ∠ORP + ∠POR = 180°
∠OPR + ∠OPR + 160 = 180
2∠OPR+ 160 = 180
2∠OPR = 180 – 160
2∠OPR = 20
∠OPR = \(\frac{20}{2}\)
∴ ∠OPR= 10°.
Question 4.
In Fig., ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
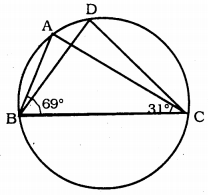
Solution:
If ∠ABC = 69°, ∠ACB = 31°, then ∠BDC = ?
In ∆ABC,
∠ABC = ∠ACB + ∠BAC = 180°
69 + 31 + ∠BAC = 180
100 + ∠BAC = 180
∠BAC = 180 – 100
∠BAC = 80°
∠BAC and ∠BDC are angles in same segment. These are equal.
∠BDC = ∠BAC = 80°
∴ ∠BDC = 80°.
Question 5.
In Fig., A, B, C, and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.
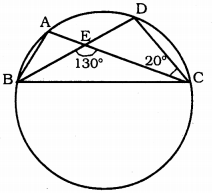
Solution:
∠BEC = 130°, ∠ECD = 20°, ∠BAC = ?
Angles formed by arc AD are ∠ABD, ∠ACD is equal.
∴ ∠ABD = ∠ACB = 20°
∠ABD = 20°
∠AEB + ∠BEC = 180 (adjacent angles)
∠AEB + 130° = 180
∠AEB = 180 – 130
∴ ∠AEB = 50°
Now, in ∆BAE,
∠BAE = ∠ABE + ∠AEB = 180°
∠BAE + 20 + 50 = 180
∠BAE + 70 = 180
∠BAE = 180 – 70
∴ ∠BAE = 110°
But ∠BAE and ∠BAC are the same.
∴ ∠BAC = 110°
Question 6.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC = 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
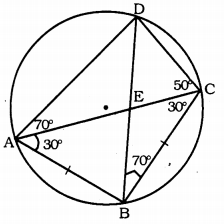
Solution:
∠DBC = 70°, ∠BAC = 30°, then ∠BCD =?
AB = BC, then ∠ECD = ?
∠DAC and ∠DBC are angles in the same segment.
∴ ∠DAC = ∠DBC = 70°
∴ ∠DAC = 70°
ABCD is a cyclic quadrilateral.
∴ Sum of opposite angles is 180°.
∠DAB + ∠DCB = 180
100 + ∠DCB = 180
[∵ ∠DAC + ∠BAC = ∠DAB 70 + 30 = 100]
∠DCB = 180 – 100
∴ ∠DCB = 80
∠DCB = ∠BCD = 80
∴ ∠BCD = 80
In ∆ABC, AB = AC,
∴ ∠BAC = ∠BCA = 30°
∠BCA = 30°
∠ECD = ∠BCD – ∠BCA = 80 – 30
∴ ∠ECD = 50°.
Question 7.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
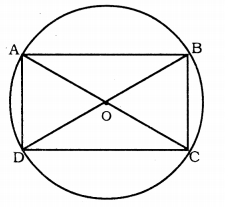
Solution:
Data: In cyclic quadrilateral ABCD, AC and BD are diameters of circle.
To Prove: ABCD is a rectangle.
Proof: AC is a diameter. ∠ABC is angle in semicircle. Angle in semicircle is a right angle.
∴ ∠ABC = 90° ∠ADC = 90°
Similarly, BD is a diamgers, ∠DAB, ∠DCB are angles in semicircle.
∠DAB = 90° ∠DCB = 90°
Now, four angles of quadrilateral ABCD are right angles.
∴ ∠A = ∠B = ∠C = ∠D = 90°
∴ ABCD is a rectangle.
Question 8.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
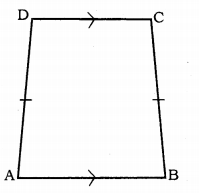
Solution:
Data: ABCD is a trapezium, DC || AB and AD = BC which are non-parallel sides.
To Prove: ABCD is a cyclic quadrilateral.
Proof: ABCD is a trapezium.
AB || CD and AD = BC.
∴ ∠DAB + ∠CDA = 180° …………. (i)
(sum of interior angles)
Similarly, ∠DCB + ∠ABC = 180° …………. (ii)
As we know, AD = BC,
∴∠DAB = ∠CBA
Substituting Eqn. (i) in Eqn. (ii),
∠CBA + ∠CDA = 180°
∠DAB + ∠DCB = 180°
If sum of angles of a quadrilateral is 180°, then it is cyclic quadrilateral.
∴ ABCD is a cyclic quadrilateral.
Question 9.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively. Prove that ∠ACP = ∠QCD.
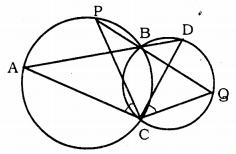
Solution:
Two circles are drawn taking PQ and PR of a triangle as diameter. Let these intersect at P and S.
To Prove: ∠ACP = ∠QCD
Proof: ∠ABP = ∠QBD ………….. (i) (vertically opposite angles)
∠ABP = ∠ACP ……….. (ii) (angles in the same segment)
Similarly, ∠QCD = ∠QBD …………. (iii)(angles in the same segment)
From (i), (ii), and (iii),
∠ACP = ∠QCD.
Question 10.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
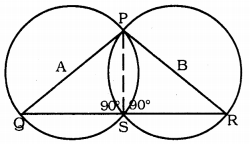
Solution:
Data: Two circles are drawn taking PQ and PR of a triangle as diameter. Let these intersect at P and S.
To Prove: The point of intersection ‘S’ is on the third side QR of ∆PQR.
Construction: Join PS.
Proof: QAP is a diameter.
∴ ∠QSP = 90° (angle in the semi-circle) Similarly, ABR is a diameter.
∠PSR – 90° (angle in the semicircle)
∠QSR = ∠QSP + ∠RSP = 90 + 90
∠QSR = 180°
∴ ∠QSR is a straight angle.
∴ QSR is a straight line.
∴ Point ‘S’ is on the third side QR of ∆PQR.
Question 11.
∆ABC and ∆ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
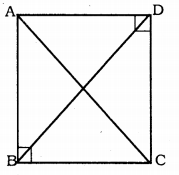
Solution:
Data: ∆ABC and ∆ADC are right-angled triangles having common hypotenuse AC.
To Prove: ∠CAD = ∠CBD
Proof: In ∆ABC, ∠ABC = 90°
∴ ∠BAC + ∠BCA = 90° …………. (i)
In ∆ADC, ∠ADC = 90°
∴ ∠DAC + ∠DCA = 90° …………… (ii)
Adding (i) and (ii),
∠BAC + ∠BCA + ∠DAC + ∠DCA = 90 + 90
(∠BAC + ∠DAC) + (∠BCA + ∠DCA) = 180°
∠BAD + ∠BCD = 180°
∴ ∠ABC + ∠ADC = 180°
If opposite angles of a quadrilateral are supplementary, then it is a cyclic quadrilateral.
∴ ∠CAD = ∠CBD (∵ Angles in the same segment).
Question 12.
Prove that a cyclic parallelogram is a rectangle.
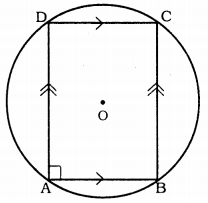
Solution:
ABCD is a cyclic parallelogram in the circle with ‘O’ centre.
To Prove: ABCD is a rectangle.
Proof: ABCD is a cyclic parallelogram.
∴ AB || DC and AD || BC
∠A = ∠C (Opposite angles of parallelogram)
But, ∠A + ∠C = 180° (Opposites angles of cyclic quadrilateral)
∠A + ∠A = 180°
2∠A = 180°
∠A = \(\frac{180}{2}\)
∴ ∠A = 90°
If each angle of the parallelogram is a right angle, it is a rectangle.
∴ ABCD is a rectangle.
KSEEB Solutions for Class 9 Maths