Students can Download Maths Chapter 6 Theorems on Triangles Additional Questions and Answers, Notes Pdf, KSEEB Solutions for Class 8 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka State Syllabus Class 8 Maths Chapter 6 Theorems on Triangles Additional Questions
Question 1.
Fill up the blanks to make the following statements true
a. Sum of the angles of a triangle in 180°
b. An exterior angle of a triangle is equal to the sum of interior opposite angles.
c. An exteior angle of a triangle is always more than either of the interior opposite angles.
d. A triangle can not have more than one right angles.
e. A triangle can not have more than one obtuse angle.
![]()
Question 2.
Choose the correct answer from the given alternatives.
a. In a triangle ABC, ∠A = 80° and AB = BAC then ∠B is __________
A. 50°
B. 60°
C. 40°
D. 70°
Solution:
A. 50°
b. In right-angled triangle, ∠A is right angle and ∠B = 35° then ∠C is _______
A. 65°
B. 55°
C. 75°
D. 45°
Solution:
B. 55°
c. In ∆ABC, ∠B = ∠C = 45°, then the triangle is ________
A. Right-angled
B. Acute angled
C. Obtuse angled
D. Equilateral triangle
Solution:
A. Right-angled
d. In an equilateral triangle, each exterior angle is ________
A. 60°
B. 90°
C. 120°
D. 150°
Solution:
C. 120°
e. Sum of the three exterior angles of a triangle is __________
A. two right angles
B. three right angles
C. one right angle
D. four right angles
Solution:
D. Four right angles
![]()
Question 3.
In a triangle ABC, ∠B = 70° find ∠A + ∠C
Solution:
∠A + ∠B + ∠C = 180° [Sum of the angles of a triangle is 180°]
∠A + 70 + ∠C = 180°
∠A + ∠C = 180° – 70
∠A + ∠C = 110°
Question 4.
In a triangle ABC, ∠A =110° and AB = AC find ∠B and ∠C
Solution:
AB = AC
∴ ∠C = ∠B [Base angles of an isosceles triangle]
∠A + ∠B + ∠C = 180° [Sum of the angles of a triangle is 180°]
110° + ∠B + ∠B = 180°
2∠B = 180 – 110
2∠B = 70°
∠B = \(\frac{70}{2}\)
∠B = 35°
∠B = ∠C = 35°
![]()
Question 5.
If three angles of a triangle are in the ratio 2 : 3 : 5 determine three angles.
Solution:
Let the common ratio be x The three angles are 2x, 3x and 5x 2x + 3x + 5x = 180° [Sum of the angles of triangle is 180°]
10x = 180°
x = \(\frac{180}{10}\)
2x = 2 ×18 = 36°
3x = 3 × 18 = 54°
5x = 5 × 18 = 90°
Question 6.
The angles of a triangle are arranged in ascending order of magnitude. If the difference between consecuttive angles is 15° find the three angles.
Solution:
Let the first angle be x then the second angle is x + 15 and third angle is x + 30.
x + x + 15 + x + 30 = 180° [Sum of the angles]
3x + 45 = 180
3x = 180 – 45
3x = 135
x = \(\frac{135}{3}\) = 45°
First angle = x = 45°
Second angle = x + 15 = 45 + 15 = 60°
Third angle = x + 30 = 45 + 30 = 75°
Question 7.
The sum of two angles of a triangle is equal to its third angle. Determine the measure of third angle.
Solution:
Let the sum of two angles be x and the third angle be y
x + y = 180° [Sum of the angles of the triangle]
y + y = 180° [∴ sum of two angles = third angle]
2y = 180°
y = \(\frac{180}{2}\)
y = 90°
∴ The third angle is 90°
![]()
Question 8.
In a triangle ABC if 2∠A = 3∠B = 6∠C determine ∠A , ∠B and ∠C
Solution:

∠A + ∠B + ∠C = 180° [Sum of the angles of a triangle]
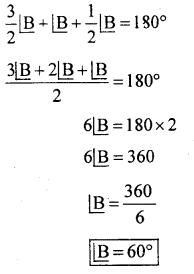

Question 9.
The angles of a triangle are x – 40°, x – 20 and \(\frac{1}{2}\) x + 15° find the value of x
Solution:
x – 40 + x – 20 + \(\frac{1}{2}\) x + 15 = 180° [Sum of the angles of a triangle]
x + x + \(\frac{1}{2}\) x – 60 + 15 = 1 80°
x + x + \(\frac{1}{2}\) x – 45 = 180°
2x + \(\frac{1}{2}\) x = 180 + 45
\(\frac{4 x+x}{2}\) = 225
5x = 225 x 2
5x = 450
x = \(\frac{450}{5}\)
x = 90°
![]()
Question 10.
In ∆ABC ∠A – ∠B = 15° and ∠B – ∠C = 30° find ∆ABC ∠A , ∠B and ∠C
Solution:
∠A – ∠B = 15°
∴ ∠A = 15 + ∠B
∠B – ∠C = 30
∴ ∠B = 30 + ∠C
∠A + ∠B + ∠C = 180° [Sum of the angle of a triangle]
15 + ∠B + ∠B + ∠C = 180° (∴ ∠A = 15 + ∠B)
15 + 2∠B + ∠C = 180°
15 + 2[30 + ∠C + ∠C = 180° (∴ ∠B = 30 + ∠C)
15 + 60 + 2∠C] + ∠C = 180°
75 + 3∠C = 180°
3∠C = 180 – 75
3∠C = 105°
∠C = \(\frac{105^{\circ}}{3}\)
∠C = 35°
Now ∠B = 30 + ∠C
∠B = 30 + 35
∠B = 65°
∠A = 15 + ∠B
∠A = 15 + 65
∠A = 180°
![]()
Question 11.
The sum of two angles of a triangle 80° and their difference is 20° find the angles of the triangle.
Solution:
Let the angles be x and y

x = \(\frac{100}{2}\) ; x = 50°
x + y = 80°
50 + y = 80°
y = 80 – 50
y = 30°
Let the third angle be z
x + y + z = 180° [Sum of the angles]
50 + 30 + z = 180°
80 + z = 180°
z = 180 – 80
z = 100°
Question 12.
In a triangle ABC, ∠B = 60°, ∠C = 80°. Suppose the bisectors of ∠B and ∠C meet at L find ∠BLC.
Solution:
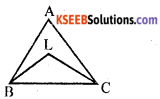
BL bisects ∠B
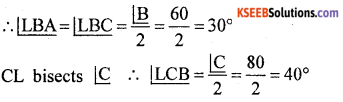
∠LBC + ∠BLC + ∠LCB = 180° (Sum of the angles of a triangle)
30 + ∠BLC + 40° = 180°
70 + ∠BLC = 180°
∠BLC = 180 – 70
∠BLC = 110°
![]()
Question 13.
In a triangle, each of the smaller angles is half of the largest angle. Find the angles.
Solution:
Let the smallest angle be x then the largest angle is 2x.
x + x + 2x = 180° [Sum of the angles of triangle]
4x = 180°
x = \(\frac{180}{4}\)
x = 45°
2x = 2 × 45° = 90°
∴ The angles are 45°, 45° and 90°
Question 14.
In a triangle each of the bigger angle is twice the third angle find the angles.
Solution:
Let the third angle be x. then the bigger angles is 2x 2x + 2x + x = 180° [Sum of the angles of triangle]
5x = 180°
x = \(\frac{180}{5}\)
x = 36°
2x = 2 × 36° = 72°
∴ The angles are 72°, 72° and 36°
Question 15.
In a triangle ABC, ∠B = 50° and ∠A = 60°. Suppose BC is extended D. Find ∠ACD
Solution
∠ACD = ∠ ABC + ∠BAC [Exterior angle = sum of interior opposite angles]
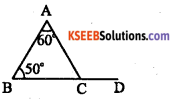
∠ACD = 50 + 60
∠ACD = 110°
Question 16.
In an isosceles triangle, the vertex angle is twice the sum of the base angles. Find the angles of the triangle.
Solution:

In ∆ABC, AB = BC
∴ ∠B = ∠C
∠Base angles of an isosceles triangle]
Given ∠A = 2(∠B + ∠C)
∠A +∠B + ∠C = 180°
[Sum of the angles of a triangle]
2(∠B + ∠C) + ∠B + ∠C = 180°
[Substituted for ∠A ]
2∠B + 2∠C + ∠B + ∠C = 180°
2∠B + 2∠B + ∠B + ∠B = 180° [∴ ∠B = ∠C]
6∠B = 180° ∠B = \(\frac{180}{6}\) = 30°
∠B = 30°, ∠C = 30° and ∠A = 2(∠B + ∠C)
= 2 (30 + 30) = 2 (60) = 120°
![]()
Question 17.
Find the sum of all the angles at the five vertices of the adjoining star.
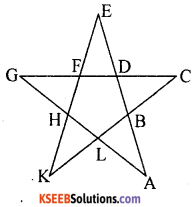
Solution:
Since all the sides of the star are equal to each other the Afes AGL, CDB, EFD, GHF and KHL are isosceles triangles. Let each base angle equal to ‘x’.
In the figure, BDFHL is a pentagon & its sides are extended in order. ∴ The sum of exterior angles = 360°
∠DBC + ∠FDE + ∠GFH + ∠KHL + ∠BLA = 360°
x + x + x + x + x = 360°
5x = 360°
x = \(\frac{360^{\circ}}{5}\) = 72°
In ∆ABL,
∠A + ∠ABL + ∠ALB = 180°
∠A + x + x = 180°
∠A + 72 + 72 = 180°
∠A + 144 = 180°
∠A = 180° – 144 ∠A = 36°
∠C, ∠E, ∠G and ∠K = 36°
∴ Sum of all the angles at the five vertices = 36° × 5 = 180°
![]()