Students can Download Basic Maths Chapter 7 Linear Inequalities Questions and Answers, Notes Pdf, 1st PUC Basic Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 1st PUC Basic Maths Question Bank Chapter 7 Linear Inequalities
Question 1.
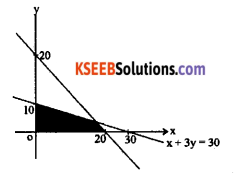
Solve graphically 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Answer:
3x + 4y = 60
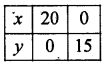
x + 3y + 30
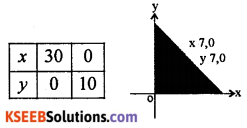
(0, 0) satisfies 3x + 4y ≤ 60 and x + 3 ≤ 30
Question 2.
Solve 2 (2x + 3) – 10 £ 6(x – 2)
Answer:
Given 2 (2x + 3) – 10 £ 6(x – 2)
⇒ 4x + 6 – 10 ≤ 6x – 12 ⇒ 4x – 4 ≤ 6x – 12
⇒ 4x – 6x ≤ – 12 + 4 ⇒ -2x ≤ -8
⇒ x ≥ \(\frac{8}{2}\) ⇒ x ∈ [4, ∞] is the solution
![]()
![]()
Question 3.
Solve the equation \(\left|\frac{2}{x-4}\right|>1\), x ≠ 4.
Answer:
we have \(\left|\frac{2}{x-4}\right|>1\), x ≠ 4
⇒ \(\frac{2}{|x-4|}>1\) ⇒ 2 > |x – 4|
⇒ 4 – 2 < x < 4 + 2
⇒ 2 < x < 6. ∴ x e (2, 6) But x 4
Question 4.
Find all pairs of consecutive even positive integers both of which are larger than 8, such that their sum is less than 25.
Answer:
Let x be the smaller of the two consecutive even positive integers, then the other even integer is x + 2.
Given x > 8 and x + (x + 2) < 25.
⇒ x > 8, and 2x + 2 < 25.
⇒ x > 8, 2x < 23 ⇒ x > 8, x < \(\frac{23}{2}\)
⇒ 8 < x < ⇒ \(\frac{23}{2}\) x = 10,
∴ the required parity even integers is (10, 12)
Question 5.
In the first four papers each of 100 marks, Ravi got 95, 72, 73, 83 marks. If he wants an average of greater than or equal to 75 marks and less than 80 marks, find the range of marks he should score in the fifth paper.
Answer:
Let score be x in the fifth paper, then
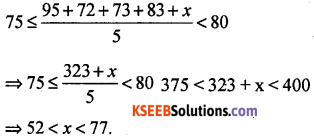
Hence Ravi must score between 52 and 77 marks.
![]()
Solve and represent the following in equalities graphically
Question 1.
x + y ≥ 4 : 2x – y > 0
Answer:
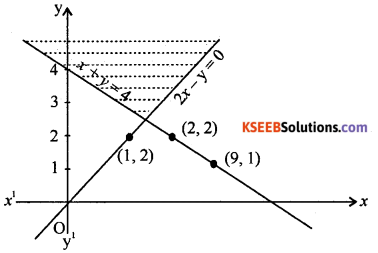
Question 2.
x + y ≤ 9, y > x, x ≥ 0
Answer:
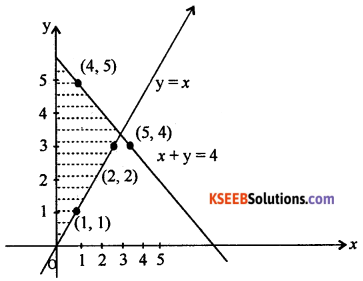
![]()
Question 3.
2x – y > 1, x – 2y < – 1
Answer:
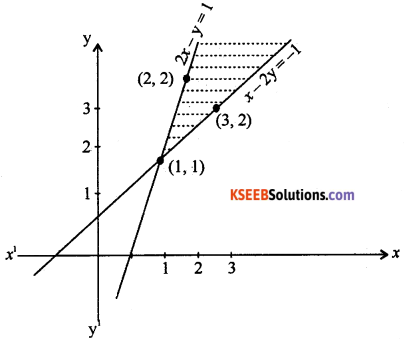
Question 4.
5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Answer:
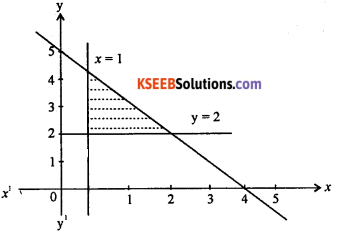
![]()
Question 5.
2x + y ≥ 4, x + y ≤ 3, 2x – y ≤ 6.
Answer:
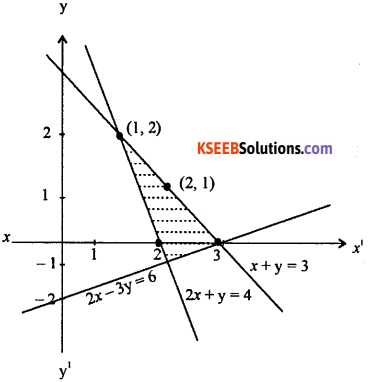
Question 6.
x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Answer:
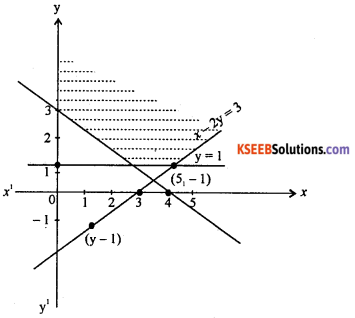
![]()
Question 7.
4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, y ≥ 0
Answer:
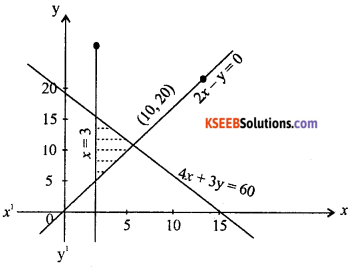
Question 8.
x + 2y ≤ 10, x + y ≥ 1, x – y ≤ 0, x ≥ 0, y ≥ 0
Answer:
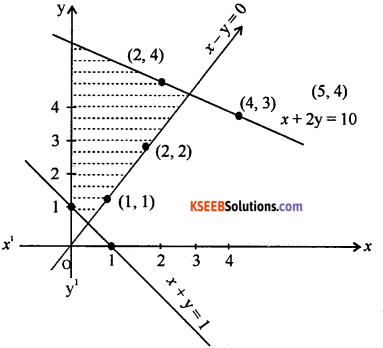
![]()
Question 9.
Solve the in equalities and represent the solutions graphically on number line.
![]()
Answer:
5(2x – 7) -3 (2x + 3) ≤ 0; 2x + 19 ≤ 6x + 47