1st PUC Maths Question Bank Chapter 13 Limits and Derivatives

Students can Download Maths Chapter 13 Limits and Derivatives Questions and Answers, Notes Pdf, 1st PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka 1st PUC Maths Question Bank Chapter 13 Limits and Derivatives

Question 1.
Explain the meaning of x → a .
Answer:
Let x be a variable and ‘a’ be a constant. Since ‘x’ is a variable we can change its value at pleasure. It can be changed so that its value comes nearer and nearer to a. Then we say that x approaches ‘a’ and it is denoted by x → a .

Question 2.
Investigate the behaviour of \(f(x)=\frac{x^{2}-4}{x-2}\) at the point the point x = 2 and near the point x = 2.
Answer:


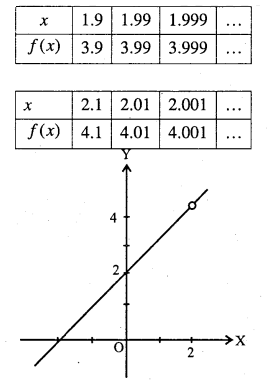
It is clear from the table that as gets nearer and nearer to 2 from either side, f(x) gets closer and closer 4 from either side.
\(\lim _{x \rightarrow 2^{-}} f(x)=\lim _{x \rightarrow 2^{+}} f(x)=4\)

Question 3.
Define limit of a function.
Answer:
Let f(x) be a function defined on an interval that contains x = a, except possible at x = a. Then we say that, \(\lim _{x \rightarrow a} f(x)=L\)
If for every number ∈ > 0 there is some number δ > 0 such that

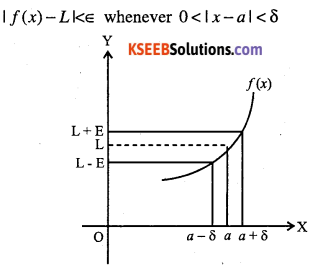
Remark: We say  \(\lim _{x \rightarrow a^{-}} f(x)\)is expected value of f at
x = a given the values of f near x to the left to a.The values is called left hand limit.

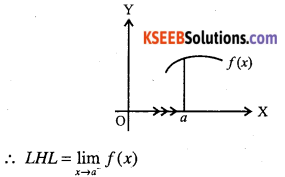
\(\text { We say } \lim _{x \rightarrow a^{+}} f(x)\) is expected value of f at x = a given the values of f near x to the right to a. The value is called right hand limit.

Question 4.
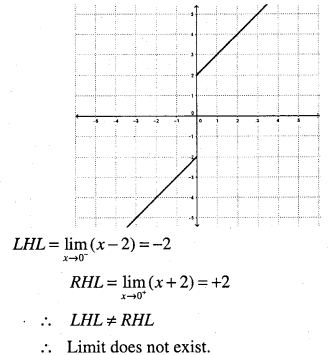
Discuss the limits of the function
\(f(x)=\left\{\begin{array}{ll}{-1,} & {\text { if } x<0} \\{1,} & {\text { if } x>0}\end{array} \text { at } x=0\right.\)
Answer:

∴ LHL ≠ RHL
Limit does not exist

Question 5.
Discuss the limit of the function f(x) = x +10 at x = 5.
Answer:

Question 6.
Discuss the limit of f(x) = x³ at x = 1.
Answer:

Question 7.
Find \(\lim _{x \rightarrow 2} f(x), \text { where } f(x)=3x\)
Answer:

Question 8.
Find \(\lim _{x \rightarrow 2} f(x)\),where f(x) = 3 a constant function
Answer:

Question 9.
Find \(\lim _{x \rightarrow 1}\left(x^{2}+x\right)\)
Answer:
\(\lim _{x \rightarrow 1}\left(x^{2}+x\right)=1^{2}+1=2\)

Question 10.
Find
\(f(x)=\left\{\begin{aligned}x-2, & x<0 \\0, & x=0 \\x+2, & x>0\end{aligned}\right.\)
Answer:

Question 11.
Find \(\lim _{x \rightarrow 1}\left(x^{3}-x^{2}+1\right)\)
Answer:
\(\lim _{x \rightarrow 1}\left(x^{3}-x^{2}+1\right)=1^{3}-1^{2}+1=1\)

Question 12.
Find \(\lim _{x \rightarrow 3} x(x+1)\)
Answer:
\(\lim _{x \rightarrow 3} x(x+1)=3(3+1)=12\)

Question 13.
Find \(\lim _{x \rightarrow-1}\left(1+x+x^{2}+\ldots+x^{10}\right)\)
Answer:

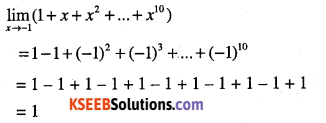
Question 14.
Find \(\begin{aligned} &\lim (x+3)\&x \rightarrow 3\end{aligned}\)
Answer:
\(\lim _{x \rightarrow 3}(x+3)=3+3=6\)

Question 15.
Find
\(\lim _{x \rightarrow \pi}\left(x-\cfrac{22}{7}\right)\)
Answer:
\(\lim _{x \rightarrow \pi}\left(x-\cfrac{22}{7}\right)=\pi-\cfrac{22}{7}\)

Question 16.
Find
\(\lim _{x \rightarrow 1} \pi r^{2}\)
Answer:
\(\lim _{x \rightarrow 1} \pi r^{2}=\pi(1)^{2}=\pi\)

Question 17.
Find
\(\lim _{x \rightarrow 4} \cfrac{4 x+3}{x-2}\)
Answer:
\(\lim _{x \rightarrow 4} \cfrac{4 x+3}{x-2}=\cfrac{4(4)+3}{4-2}=\cfrac{19}{2}\)

Question 18.
Find
\(\lim _{x \rightarrow-1} \cfrac{x^{10}+x^{5}+1}{x-1}\)
Answer:

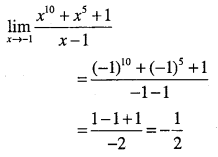
Question 19.
Find
\(\lim _{x \rightarrow 0} \cfrac{(x+1)^{2}-1}{x}\)
Answer:

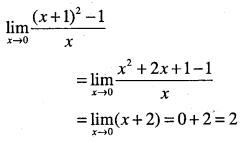
Question 20.
Find
\(\lim _{x \rightarrow 2} \cfrac{3 x^{2}-x-10}{x^{2}-4}\)
Answer:

Question 21.
Find
\(\lim _{x \rightarrow 3} \cfrac{x^{4}-81}{2 x^{2}-5 x-3}\)
Answer:

Question 22.
Find
\(\lim _{x \rightarrow 0} \cfrac{a x+b}{c x+1}\)
Answer:

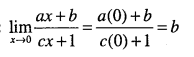
Question 23.
Find
\(\lim _{x \rightarrow 1} \cfrac{a x^{2}+b x+c}{c x^{2}+b x+a}, a+b+c \neq 0\)
Answer:

Question 24.
Find
\(\lim _{x \rightarrow 2} \cfrac{\cfrac{1}{x}+\cfrac{1}{2}}{x+2}\)
Answer:

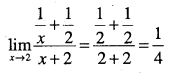
Question 25.
Find
\(\lim _{x \rightarrow 1} \cfrac{x^{2}+1}{x+100}\)
Answer:

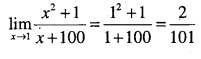
Question 26.
Find
\(\lim _{x \rightarrow 2} \cfrac{x^{3}-4 x^{2}+4 x}{x^{2}-4}\)
Answer:

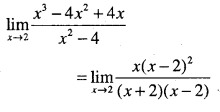
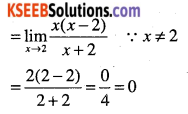
Question 27.
Find
\(\lim _{x \rightarrow 2} \cfrac{x^{2}-4}{x^{3}-4 x^{2}+4 x}\)
Answer:

Question 28.
Find
\(\lim _{x \rightarrow 2} \cfrac{x^{3}-2 x^{2}}{x^{2}-5 x+6}\)
Answer:

Question 29.
Find
\(\lim _{x \rightarrow 1}\left[\cfrac{x-2}{x^{2}-x}-\cfrac{1}{x^{3}-3 x^{2}+2 x}\right]\)
Answer:

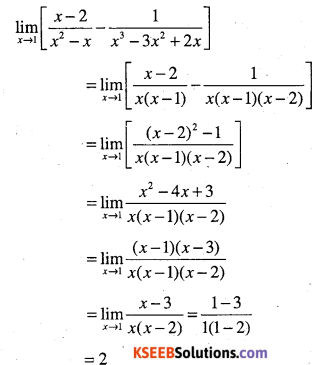
Question 30.
Prove that,for any positive integer n,
\(\lim _{x \rightarrow a} \cfrac{x^{n}-a^{n}}{x-a}=n\left(a^{n-1}\right)\)
Answer:

Question 31.
Find
\(\lim _{x \rightarrow a} \cfrac{x^{3}-a^{3}}{x-a}\)
Answer:
\(\lim _{x \rightarrow a} \cfrac{x^{3}-a^{3}}{x-a}=3 a^{2}\)

Question 32.
Find
\(\lim _{x \rightarrow 2} \cfrac{x^{7}-128}{x-2}\)
Answer:

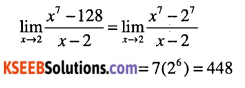
Question 33.
Find
\(\lim _{x \rightarrow 1} \cfrac{x^{3}-1}{x-1}\)
Answer:

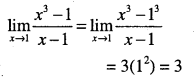
Question 34.
Find
\(\lim _{x \rightarrow a} \cfrac{x^{2 / 7}-a^{2 / 7}}{x-a}\)
Answer:

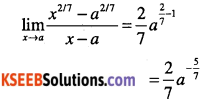
Question 35.
Find
\(\lim _{x \rightarrow-a} \cfrac{x^{5}+a^{5}}{x+a}\)
Answer:

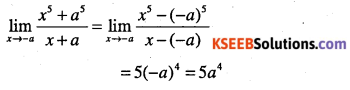
Question 36.
Find
\(\lim _{x \rightarrow-1} \cfrac{x^{3}+1}{x+1}\)
Answer:

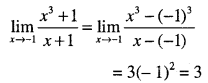
Question 37.
Find
\(\lim _{x \rightarrow a} \cfrac{x \sqrt{x}-a \sqrt{a}}{x-a}\)
Answer:

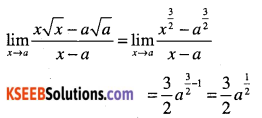
Question 38.
Find
\(\lim _{2 x \rightarrow-1} \cfrac{8 x^{3}+1}{2 x+1}\)
Answer:

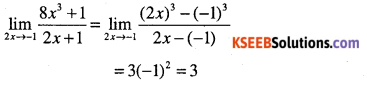
Question 39.
Find
\(\lim _{x \rightarrow 1} \cfrac{x^{15}-1}{x^{10}-1}\)
Answer:

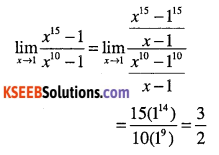
Question 40.
Find
\(\lim _{x \rightarrow 2} \cfrac{x^{3}-8}{x^{2}-4}\)
Answer:

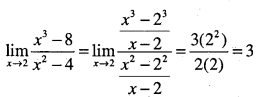
Question 41.
Find
\(\lim _{x \rightarrow 4} \cfrac{x^{3}-64}{x^{2}-16}\)
Answer:

Question 42.
Find
\(\lim _{x \rightarrow 2} \cfrac{x^{10}-1024}{x^{5}-32}\)
Answer:

Question 43.
Find
\(\lim _{x \rightarrow 9} \cfrac{x^{\cfrac{3}{2}}-27}{x-9}\)
Answer:

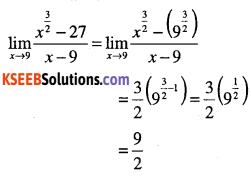
Question 44.
Find
\(\lim _{x \rightarrow a} \cfrac{x^{\cfrac{2}{3}}-a^{\cfrac{2}{3}}}{x^{\cfrac{3}{4}}-a^{\cfrac{3}{4}}}\)
Answer:

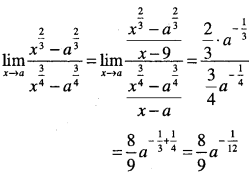
Question 45.
\(\lim _{x \rightarrow 0} \cfrac{\sqrt{1+x}-1}{x}\)
Answer:

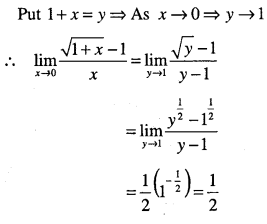
Question 46.
Find
\(\lim _{z \rightarrow 1} \cfrac{z^{\cfrac{1}{3}}-1}{z^{\cfrac{1}{6}}-1}\)
Answer:

Question 47.
Find
\(\lim _{x \rightarrow 0} \cfrac{(1-x)^{n}-1}{x}\)
Answer:

Question 48.
Find
\(\lim _{x \rightarrow 1} \cfrac{\left(x+x^{2}+x^{3}+\ldots+x^{n}\right)-n}{x-1}\)
Answer:

Result 1:
Let f and g be two real valued functions with the same domain such that f(x) ≤ g(x), for all x in the domain of definition. For some a, if both
\(\lim _{x \rightarrow a} f(x)\)and \(\lim _{x \rightarrow a} g(x)\) exists them. \(\lim _{x \rightarrow a} f(x) \leq \lim _{x \rightarrow a} g(x)\)

Result 2 : (Sandwich theorem):
Let f, g and h be real functions such that f(x)≤g(x)≤h(x),∀x, in common domain of definition. For some real number a
\(\lim _{x \rightarrow a} f(x)=l=\lim _{x \rightarrow a} h(x) \text { then } \lim _{x \rightarrow a} g(x)=1\)

Question 49.
Prove that
\(\lim _{x \rightarrow 0} \cfrac{\sin x}{x}=1\)
Answer:


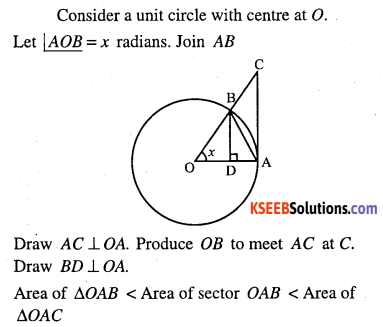
Question 50.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\sin a x}{b x}\)
Answer:

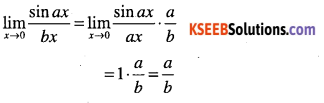
Question 51.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\sin a x}{\sin b x}, a, b \neq 0\)
Answer:

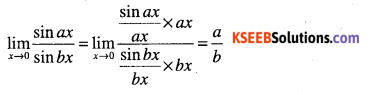
Question 52.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\sin 4 x}{\sin 6 x}\)
Answer:

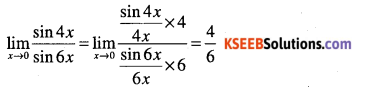
Question 53.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\tan x}{x}\)
Answer:

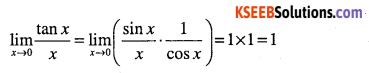
Question 54.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\tan 3 x}{\sin 2 x}\)
Answer:

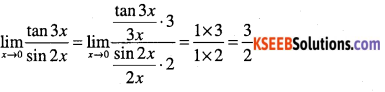
Question 55.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\tan 8 x}{\sin 2 x}\)
Answer:

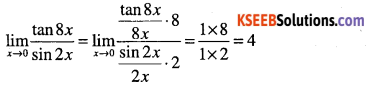
Question 56.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\sin 5 x}{\tan 3 x}\)
Answer:

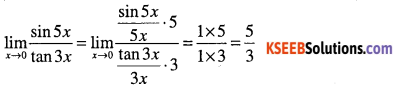
Question 57.
Evaluate:
\(\lim _{x \rightarrow \pi} \cfrac{\sin (\pi-x)}{\pi(\pi-x)}\)
Answer:

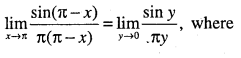
Question 58.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\cos x}{\pi-x}\)
Answer:

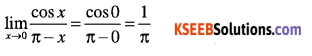
Question 59.
Evaluate:
\(\lim _{\theta \rightarrow 0} \cfrac{1-\cos 4 \theta}{1-\cos 6 \theta}\)
Answer:

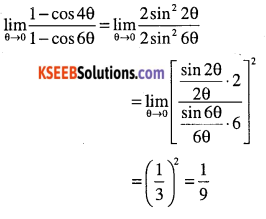
Question 60.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{1-\cos 5 x}{1-\cos 6 x}\)
Answer:

Question 61.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{1-\cos 3 x}{x^{2}}\)
Answer:

Question 62.
Evaluate:
\(\lim _{\theta \rightarrow 0} \cfrac{1-\cos \theta}{2 \theta^{2}}\)
Answer:

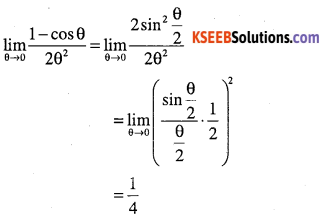
Question 63.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{1-\cos x}{x}\)
Answer:

Question 64.
Evaluate:
\(\begin{aligned}&\lim x \cdot \sec x\\&x \rightarrow 0\end{aligned}\)
Answer:

Question 65.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{a x+x \cos x}{b \sin x}\)
Answer:

Question 66.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\sin a x+b x}{a x+\sin b x}, a, b, a+b \neq 0\)
Answer:

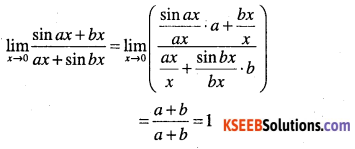
Question 67.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{1-\cos x}{\sin ^{2} x}\)
Answer:

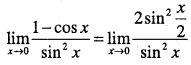
Question 68.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{1-\cos 2 x}{3 \tan ^{2} x}\)
Answer:

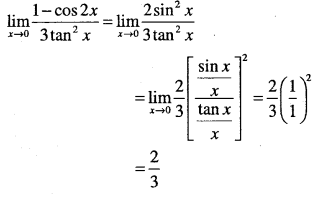
Question 69.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\tan 2 x+\sin 2 x}{x}\)
Answer:

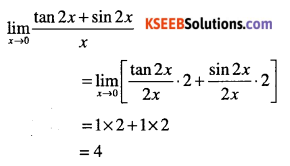
Question 70.
Evaluate:
\(\lim _{x \rightarrow 0}[\csc x-\cot x]\)
Answer:

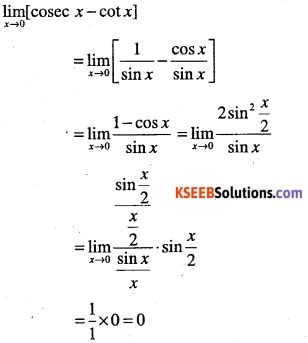
Question 71.
Evaluate:
\(\lim _{x \rightarrow \cfrac{\pi}{2}} \cfrac{\tan 2 x}{x-\cfrac{\pi}{2}}\)
Answer:

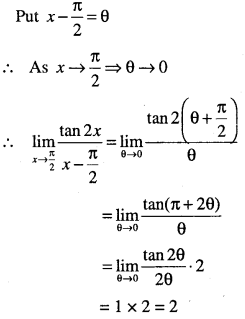
Question 72.
\(\begin{aligned} &\text { Find } \lim _{x \rightarrow 0} f(x) \text { and } \lim _{x \rightarrow 1} f(x) \text { if }\\&f(x)=\left\{\begin{array}{ll}{2 x+3,} & {x \leq 0} \\{3(x+1),} & {x>0}\end{array}\right.\end{aligned}\)
Answer:

Question 73.
Find
\(\lim _{x \rightarrow 1} f(x), \text { where } f(x)=\left\{\begin{array}{cc}{x^{2}-1,} & {x \leq 1} \\{-x^{2}-1,} & {x>1}\end{array}\right.\)
Answer:

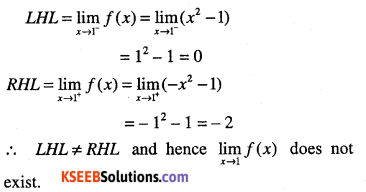
Question 74.
Evaluate
\(\lim _{x \rightarrow 0} f(x), \text { where } f(x)=\left\{\begin{array}{cc}{\frac{|x|}{x},} & {x \neq 0} \\{0,} & {x=0}\end{array}\right.\)
Answer:

Question 75.
Find
\(\lim _{x \rightarrow 5} f(x), \text { where } f(x)=|x|-5\)
Answer:

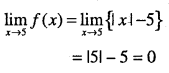
Question 76.
Suppose
\(f(x)=\left\{\begin{array}{cl}{a+b x,} & {x<1} \\{4,} & {x=1 \text { and }} \\{b-a x,} &{x>1}\end{array}\right.\)
\(\lim _{x \rightarrow 1} f(x)=f(1)\).what are possible value of a and b?
Answer:

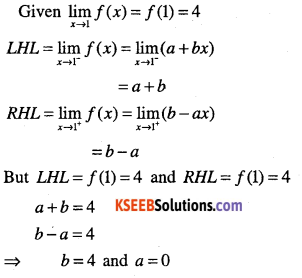
Question 77.
Let a₁, a₂,…, a_n be fixed real numbers and define a function
f(x) = (x – a₁)(x – a₂)…(x – a_n).
\(\text { What is } \lim _{x \rightarrow a_{1}} f(x) ? \text { For some } a \neq a_{1}, a_{2}, \dots, a_{n}\) \(\text { 1) }\)
Answer:

Question 78.
\(\begin{aligned}&\text { If } f(x)=\left\{\begin{aligned}|x|+1, & x<0 \\0, & x=0 \text { for what value(s) of } \\|x|-1, & x>0\end{aligned}\right.\\&^{t} a^{\prime} \text { does } \lim _{x \rightarrow a} f(x) \text { exists? }\end{aligned}\)
Answer:

Question 79.
If the function f(x) satisfies \(\lim _{x \rightarrow 1} \frac{f(x)-2}{x^{2}-1}=\pi, \text { evaluate } \lim _{x \rightarrow 1} f(x)\)
Answer:

Question 80.
If \(f(x)=\left\{\begin{array}{cc}{m x^{2}+n,} & {x<0} \\{n x+m,} & {0 \leq x \leq 1} \\{n x^{3}+m,} & {x>1}\end{array}\right.\)for what integers m and n does both
\(\lim _{x \rightarrow 0} f(x)\)\(\lim _{x \rightarrow 1} f(x) \text { exist? }\)
Answer:

Derivaties:

Question 81.
Define a derivative of f(x) at a point.
Ans :
Suppose f is a real valued function and ‘a’ is a point in its domain of definition. The derivative of f at ‘a’ is defined by

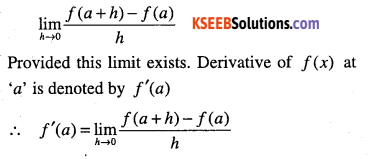
Question 82.
Find the derivative at x = 2 of the function f(x) = 3x.
Answer:
We have

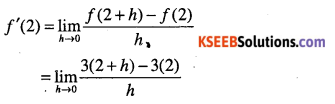
Question 83.
Find the derivative of f(x) = x² – 2 at x = 10.
Answer:
We have,

Question 84.
Find the derivative of 99x at x = 100.
Answer:
We have,

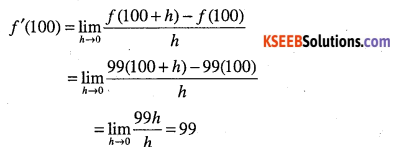
Question 85.
Find the derivative of x at x = 1.
Answer:
We have,

Question 86.
Find the derivative of the function f(x) = 2x² + 3x – 5 at x = -1. Also prove that
f'(0) + 3f'(l) = 0.
Answer:
We have,

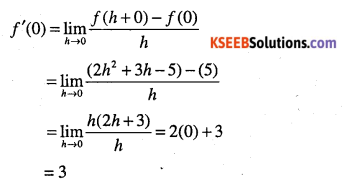
Question 87.
Find the derivative of sinx at x = 0.
Answer:

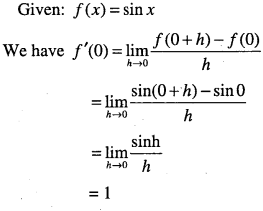
Question 88.
Find the derivative of f(x) = 3 at x = 3
Answer:

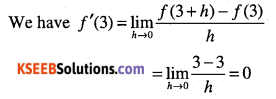
Question 89.
Define derivative of f(x) at x.
Answer:
Suppose f is a real valued function, the function defined by\(\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\),wherever the limit exists is defined to be derivative of f at x and is denoted by f'(x). Thus \(f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)

Question 90.
Find the derivative of f(x) = 10x
Answer:

Question 91.
Find the derivative of the following : (by first principles)

Answer:

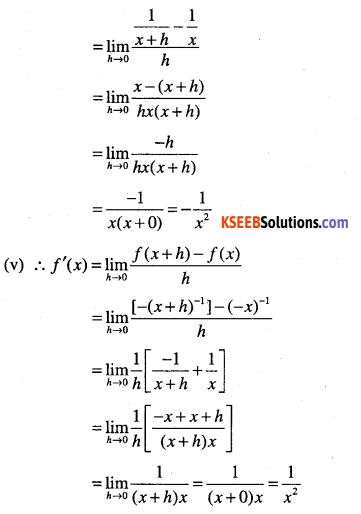
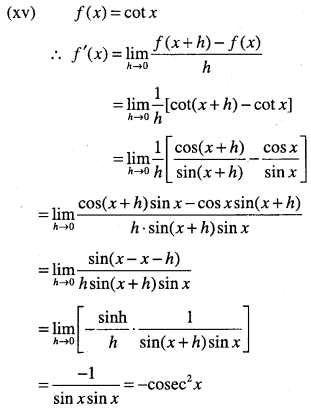
Algebra of derivative of functions

Theorem

Let f and g be two functions such that their derivatives are defined in a common domain. Then

(i) Derivative of sum of two functions is sum of the derivatives of the functions.
\(\cfrac{d}{d x}[f(x)+g(x)]=\cfrac{d}{d x} f(x)+\cfrac{d}{d x} g(x)\)

(ii) Derivative of difference of two functions is difference of the derivatives of the functions
\(\cfrac{d}{d x}[f(x)-g(x)]=\cfrac{d}{d x} f(x)-\cfrac{d}{d x} g(x)\)

(iii) Derivative of product of two functions is given by the following product rule:
\(\begin{aligned}\cfrac{d}{d x}[f(x) \cdot g(x)] & \\&=f(x)\left[\cfrac{d}{d x}g(x)\right]+g(x)\left[\cfrac{d}{d x} f(x)\right]\end{aligned}\)

(iv) Derivative of the quotient of two functions is given by the following quotient rule:
\(\cfrac{d}{d x} \cfrac{f(x)}{g(x)}=\cfrac{g(x) \cfrac{d}{d x} f(x)-f(x) \cfrac{d}{d x} g(x)}{[g(x)]^{2}}\)

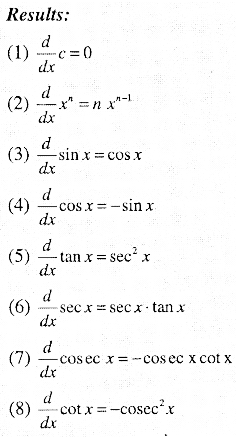
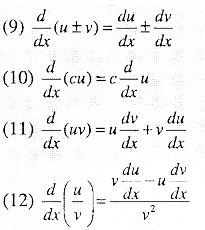
I. Differentiate the following with respect to x

Question 1.
y = 25
Answer:
\(\cfrac{d y}{d x}=0\)

Question 2.
\(y=\cfrac{\pi}{4}\)
Answer:
\(\cfrac{d y}{d x}=0\)

Question 3.
y = 5 cos α, α is a constant.
Answer:
\(\cfrac{d y}{d x}=0\)

Question 4.
\(y=x^{6}\)
Answer:
\(\cfrac{d y}{d x}=6 x^{5}\)

Question 5.
\(y=x^{-5}\)
Answer:
\(\cfrac{d y}{d x}=-5 x^{-6}\)

Question 6.
\(y=5 x^{\frac{7}{2}}\)
Answer:
\(\cfrac{d y}{d x}=5 \cdot \cfrac{7}{2} x^{\cfrac{7}{2}-1}=\cfrac{35}{2} x^{\cfrac{5}{2}}\)

Question 7.
\(y=8 \cdot x^{\cfrac{5}{2}} x^{-\cfrac{5}{3}}\)
Answer:

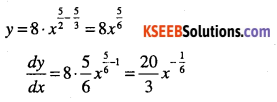
Question 8.
y = ( 2 + x)²
Answer:

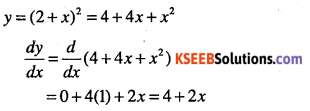
Question 9.
\(y=\frac{3}{x^{5}}\)
Answer:

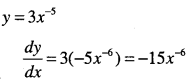
Question 10.
\(y=\left(x+\cfrac{1}{x}\right)^{2}, x \neq 0\)
Answer:

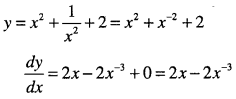
Question 11.
\(y=\left(\sqrt{x}+\cfrac{1}{\sqrt{x}}\right)^{2}\)
Answer:

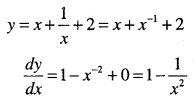
Question 12.
y = (ax)^m +b^m
Answer:

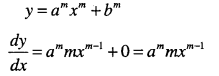
Question 13.
y = x³+ 4x² +7x + 2
Answer:

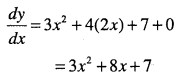
Question 14.
\(y=3+4 x-7 x^{2}-\sqrt{2} x^{3}+\pi x^{4}-\cfrac{2}{5} x^{5}\)
Answer:

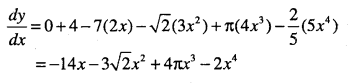
Question 15.
\(y=2 x^{\cfrac{1}{2}}+6 x^{\cfrac{1}{3}}+2 x^{\cfrac{3}{2}}\)
Answer:

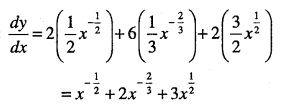
Question 16.
\(y=x^{n}+a x^{n-1}+a^{2} x^{n-2}+\ldots+a^{n-1} x+a^{n}\)
Answer:

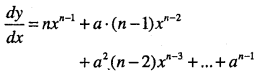
Question 17.
\(y=(x-2)^{2}(2 x-3)\)
Answer:

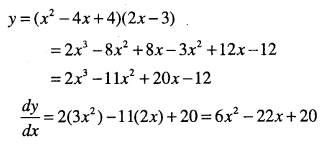
Question 18.
\(y=\cfrac{(x+5)\left(2 x^{2}-1\right)}{x}\)
Answer:

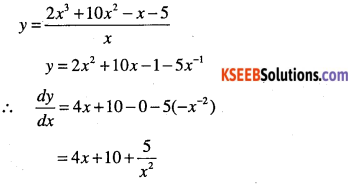
Question 19.
\(y=\left(2 x^{2}+3\right)\left(x^{2}-x+2\right)\)
Answer:

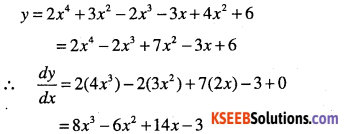
Question 20.
\(y=\cfrac{3 x^{7}+x^{5}-2 x^{4}+x-3}{x^{4}}\)
Answer:

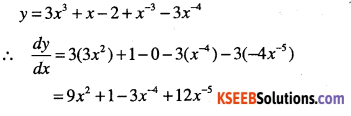
Question 21.
\(y=\cfrac{(2 x-1)\left(5 x^{\cfrac{1}{2}}+7\right)}{x^{\cfrac{1}{2}}}\)
Answer:

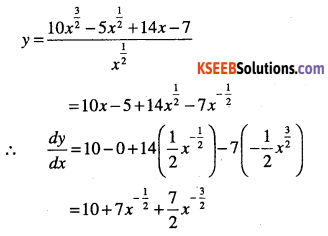
Question 22.
\(y=\left(x-\cfrac{1}{x}\right)\left(x^{2}-\cfrac{1}{x^{2}}\right)\)
Answer:

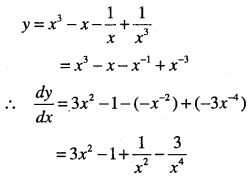
Question 23.
\(y=\cfrac{2 x^{2}-3 x+1}{\sqrt{x}}\)
Answer:

Question 24.
\(y=x^{4}+7 x^{3}+8 x^{2}+3 x+2+\sqrt{x}+\frac{1}{\sqrt{x}}\)
Answer:

Question 25.
y = a(x -2)(x – 3) + b
Answer:

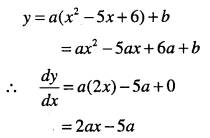
Question 26.
y = a(x – 2) (x – b)
Answer:

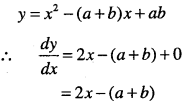
Question 27.
y = (ax²+b)²
Answer:
y = (ax² + b)²
= a²x⁴ + 2abx² + b²

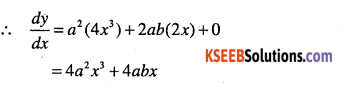
Question 28.
y = x + a
Answer:
\(\cfrac{d y}{d x}=1+0=1\)

Question 29.
\(y=4 \sqrt{x}-2\)
Answer:
\( \cfrac{d y}{d x}=4\left(\cfrac{1}{2} x^{-\cfrac{1}{2}}\right)-0=2 x^{-\cfrac{1}{2}}\)

Question 30.
\(y=(p x+q)\left(\frac{r}{x}+s\right)\)
Answer:

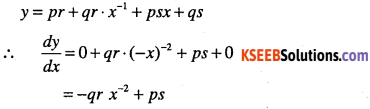
Question 31.
\(y=\cfrac{a}{x^{4}}-\cfrac{b}{x^{2}}+\cos x\)
Answer:

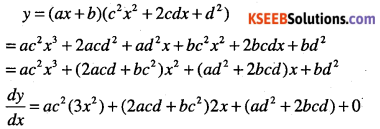
Question 32.
\(y=\cfrac{a}{x^{4}}-\cfrac{b}{x^{2}}+\cos x\)
Answer:

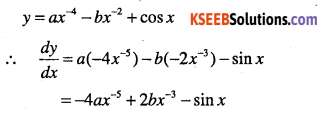
Question 33.
y = sin (x  + a)
Answer:

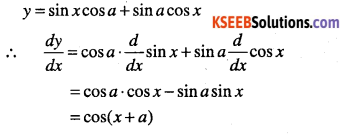
Question 34.
For the function
\(\begin{aligned}&f(x)=\cfrac{x^{100}}{100}+\cfrac{x^{99}}{99}+\ldots+\cfrac{x^{2}}{2}+x+1 . \text { Prove that }\\&f^{\prime}(1)=100 f^{\prime}(0)\end{aligned}\)
Answer:

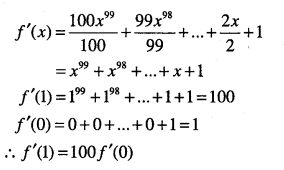
II. Using product rule,differentiate the following with respect to x:

Question 1.
y =x sin x
Answer:

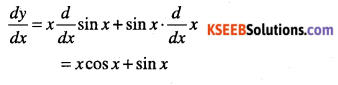
Question 2.
y = x cos x
Answer:

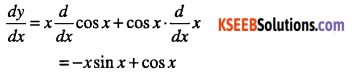
Question 3.
y = x³ sin x
Answer:

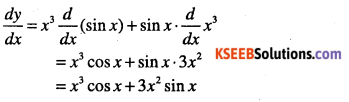
Question 4.
y = (x – 2)(x + 3)
Answer:

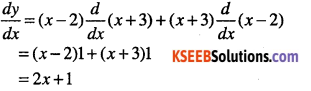
Question 5.
y = sinx cosx
Answer:

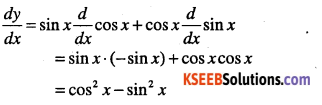
Question 6.
y = sec x tan x
Answer:

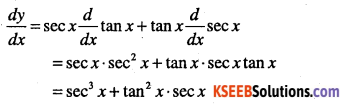
Question 7.
y = cosec x cot x
Answer:

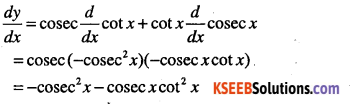
Question 8.
y = x⁵ cot x
Answer:

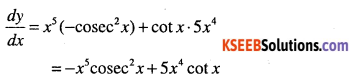
Question 9.
y = xⁿ tan x
Answer:

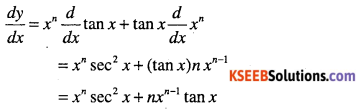
Question 10.
y = (x³ + x² + 1)sin x
Answer:

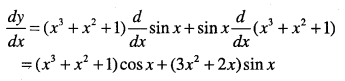
Question 11.
y = (x² -5x + 6)sec x
Answer:

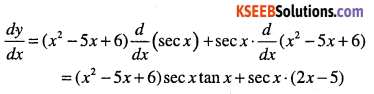
Question 12.
y = (x² +1)cosx
Answer:

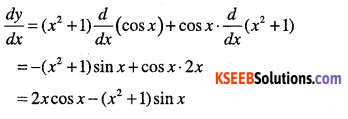
Question 13.
x = sin 2x
Answer:

Question 14.
y = (5x³ 4- 3x -1)(x -1)
Answer:

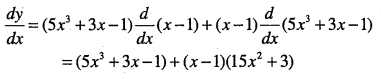
Question 15.
y = x^-3(5 + 3x)
Answer:

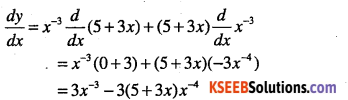
Question 16.
y = x⁵(3-6x^-9)
Answer:

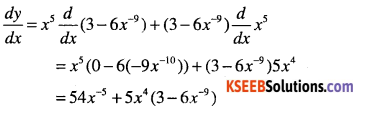
Question 17.
y = x^-4(3 – 4^-5)
Answer:

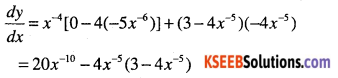
Question 18.
y = (x² – 5x + 6)(x³ + 2)
Answer:

Question 19.
y = x⁴(5 sin x -3 cos x)
Answer:

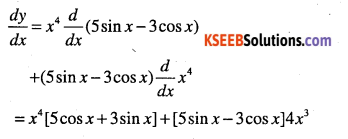
Question 20.
y = (x+ sec x)(x – tanx)
Answer:

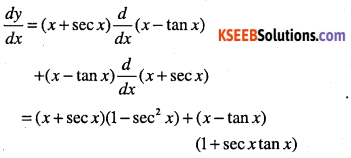
Question 21.
y = (5 – 4 cosx)(1 – 2tanx)
Answer:

Question 22.
y = (1 + 2 tan x)(5 + 4 cos x)
Answer:

Question 23.
y = (x + cos x)(x – tanx)
Answer:

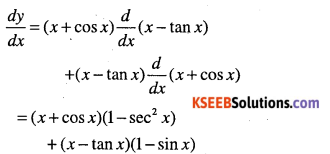
Question 24.
y = (x + sec x)(x -tan x)
Answer:

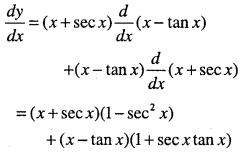
Question 25.
y= (ax² + sinx)(p + q cos x)
Answer:

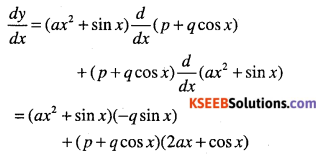
III. Using quotient rule, differentiable with respect to x

Question 1.
y = cot x
Answer:

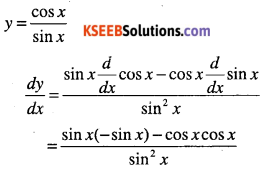
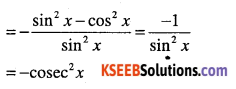
Question 2.
\(y=\cfrac{x^{n}-a^{n}}{x-a}\)
Answer:

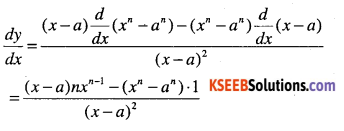
Question 3.
\(y=\cfrac{1+x^{2}}{1-x^{2}}\)
Answer:

Question 4.
\(y=\cfrac{7 x+4}{4 x-7}\)
Answer:

Question 5.
\(y=\cfrac{x}{x+5}\)
Answer:

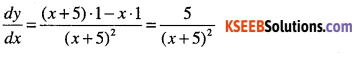
Question 6.
\(y=\cfrac{x-a}{x-b}\)
Answer:

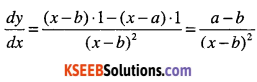
Question 7.
\(y=\cfrac{2 x+3}{x-2}\)
Answer:

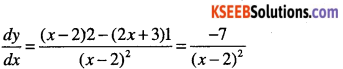
Question 8.
\(y=\cfrac{a x+b}{c x+d}\)
Answer:

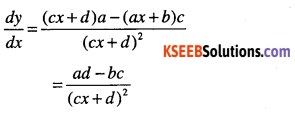
Question 9.
\(y=\cfrac{1+\cfrac{1}{x}}{1-\cfrac{1}{x}}\)
Answer:

Question 10.
\(y=\cfrac{x^{2}+5 x-6}{4 x^{2}-x+3}\)
Answer:

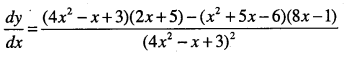
Question 11.
\(y=\cfrac{x^{2}-1}{x^{2}+7 x+1}\)
Answer:

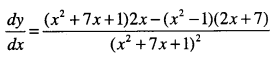
Question 12.
\(y=\cfrac{(x-1)(x-2)}{(x-3)(x-4)}\)
Answer:

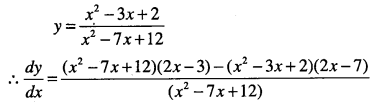
Question 13.
\(y=\cfrac{\sqrt{a}+\sqrt{x}}{\sqrt{a}-\sqrt{x}}\)
Answer:

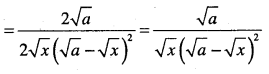
Question 14.
\(y=\cfrac{a x^{2}+b x+c}{p x^{2}+q x+r}\)
Answer:

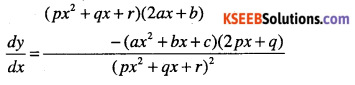
Question 15.
\(y=\cfrac{a x+b}{p x^{2}+q x+r}\)
Answer:

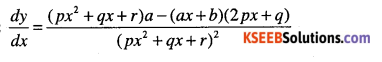
Question 16.
\(y=\cfrac{p x^{2}+q x+r}{a x+b}\)
Answer:

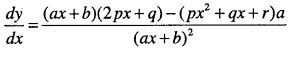
Question 17.
\(y=\cfrac{1}{p x^{2}+q x+r}\)
Answer:

Question 18.
\(y=\cfrac{1}{a x^{2}+b x+c}\)
Answer:

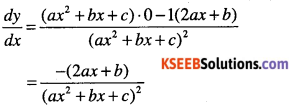
Question 19.
\(y=\cfrac{\sec x+1}{\sec x-1}\)
Answer:

Question 20.
\(y=\cfrac{1-\tan x}{1+\tan x}\)
Answer:

Question 21.
\(y=\cfrac{\sec x-1}{\sec x+1}\)
Answer:

Question 22.
\(y=\cfrac{a+b \sin x}{c+d \cos x}\)
Answer:

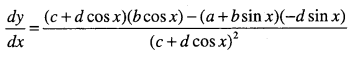
Question 23.
\(y=\cfrac{4 x+5 \sin x}{3 x+7 \cos x}\)
Answer:

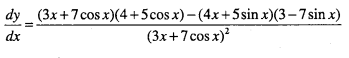
Question 24.
\(y=\cfrac{a+\sin x}{1+a \sin x}\)
Answer:

Question 25.
\(y=\cfrac{x^{5}-\cos x}{\sin x}\)
Answer:

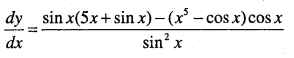
Question 26.
\(y=\cfrac{x+\cos x}{\tan x}\)
Answer:

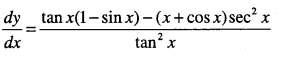
Question 27.
\(y=\cfrac{\cos x}{1+\sin x}\)
Answer:

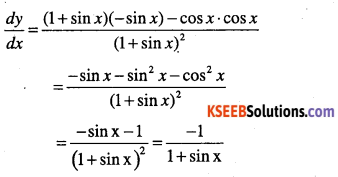
Question 28.
\(y=\cfrac{\sin x+\cos x}{\sin x-\cos x}\)
Answer:

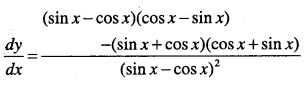
Question 29.
\(y=\frac{x^{2} \cos \frac{\pi}{4}}{\sin x}\)
Answer:

Question 30.
\(y=\cfrac{x^{2} \cos \cfrac{\pi}{4}}{\sin x}\)
Answer:

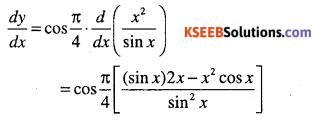
Limits involving exponential and Logarithmic functions:

Question 1.
Define a logarithmic function.
Answer:
The logarithmic function expressed as log_e: R⁺ → R is given by log_e x = y, if and only if e^y = x

Question 2.
Prove that \(\lim _{x \rightarrow 0} \cfrac{e^{x}-1}{x}=1\)
Answer:

Question 3.
Prove that
\(\lim _{x \rightarrow 0} \cfrac{\log _{e}(1+x)}{x}=1\)
Answer:
\(\text { Let } \frac{\log _{e}(1+x)}{x}=y . \text { Then }\)

Question 4.
Compute
\(\lim _{x \rightarrow 0} \cfrac{e^{3 x}-1}{x}\)
Answer:

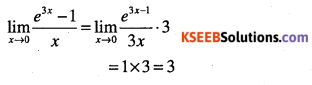
Question 5.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{e^{4 x}-1}{x}\)
Answer:

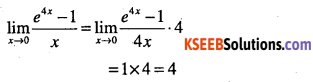
Question 6.
Compute
\(\lim _{x \rightarrow 0} \cfrac{e^{2+x}-e^{2}}{x}\)
Answer:

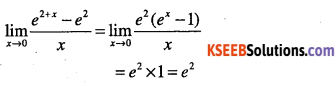
Question 7.
Compute
\(\lim _{x \rightarrow 0} \frac{e^{\sin x}-1}{x}\)
Answer:

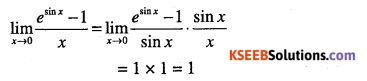
Question 8.
Compute
\(\lim _{x \rightarrow 0} \cfrac{e^{x}-\sin x-1}{x}\)
Answer:

Question 9.
Evalute
\(\lim _{x \rightarrow 5} \cfrac{e^{x}-e^{5}}{x-5}\)
Answer:

Question 10.
Compute:
\(\lim _{x \rightarrow 3} \frac{e^{x}-e^{3}}{x-3}\)
Answer:

Question 11.
\(\lim _{x \rightarrow 0} \cfrac{x\left(e^{x}-1\right)}{1-\cos x}\)
Answer:

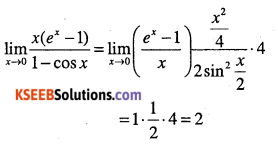
Question 12.
Evaluate:
\(\lim _{x \rightarrow 0} \cfrac{\log _{e}(1+2 x)}{x}\)
Answer:

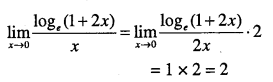
Question 13.
Evaluate:
\(\lim _{x \rightarrow 0} \frac{\log \left(1+x^{3}\right)}{\sin ^{3} x}\)
Answer:

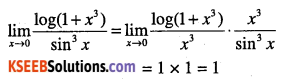
Question 14.
Evaluate
\(\lim _{x \rightarrow 1} \cfrac{\log _{e} x}{x-1}\)
Answer: