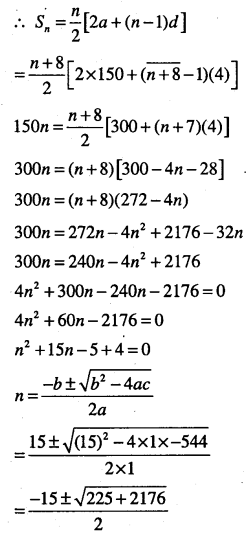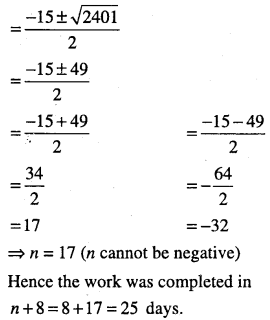Students can Download Maths Chapter 9 Sequences and Series Questions and Answers, Notes Pdf, 1st PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 1st PUC Maths Question Bank Chapter 9 Sequences and Series
Question 1.
Define sequence of numbers.
Answer :
Arrangement of numbers one after another, according to some rule is called a sequence of numbers. OR Sequence is a real valued function whose domain is set of all natural numbers.
Note:
- The numbers in the sequence are called terms.
- The nth term of the sequence is denoted by tn or Tn or an.
Question 2.
Define finite and infinite sequence.
Answer :
The sequence which has finite number of terms, then it is called finite sequence.
The sequence which has infinite number of terms, then it is called infinite sequence.
![]()
Problems
Question 1.
Write the first five terms of each of the sequences whose nth terms are
(i) an = n(n + 2)
(ii) \(a_{n}=\frac{n}{n+1}\)
(iii) \(a_{n}=2^{n}\)
(iv) \( a_{n}=\frac{2 n-3}{6}\)
(v) \(a_{n}=(-1)^{n-1} \cdot 5^{n+1}\)
(v)\(a_{n}=n\left(\frac{n^{2}+5}{4}\right)\)
Answer:

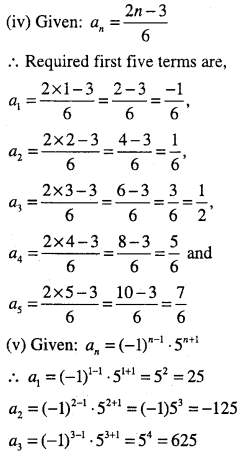

Question 2.
Find the indicated terms in each of the following sequences whose nth terms are given
(i) \(a_{n}=4 n-3 ; a_{17}, a_{24}\)
(ii)\(a_{n}=\frac{n^{2}}{2^{n}} ; a_{7}\)
(iii)\(a_{n}=(-1)^{n-1} \cdot n^{3} ; a_{9}\)
(iv) \(a_{n}=\frac{n(n-2)}{n+3} ; a_{20}\)
Answer:

![]()
Question 3.
Write the first five terms of the sequences and obtain the corresponding series.
(i)\(a_{1}=3, a_{n}=3 a_{n-1}+2, \text { for all } n>1\)
(ii) \(a_{1}=-1, a_{n}=\frac{a_{n-1}}{n}, n \geq 2\)
(iii)\(a_{1}=a_{2}=2, a_{n}=a_{n-1}-1, n>2\)
Answer:
(i) Given a1 = 3, an = 3an-1 + 2, for all n > 1
Substituting n = 2, 3, 4, 5 we get
a2 = 3(a1 +2 = 3(3) +2 = 11
a3 = 3(a2) + 2 = 3(11) + 2
= 33 + 2 = 35
a4 = 3(a3) + 2 = 3(35) + 2
= 105 + 2 = 107 a5
= 3(a4) + 2 = 3(107) + 2
= 321 + 2 = 323
∴ Required five terms are ax = 3,
a2= 11, a3 = 35, a4 = 107, a5 = 323
Hence, the corresponding series is
3 + 11 + 35 + 107 + 323 +………………….

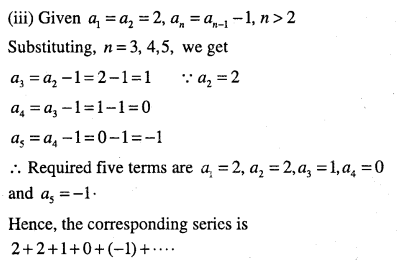
Question 4.
The Fibonacci sequence is defined by 1 = a1= a2 and an=an-1+an-2, n> 2. Find
\(\frac{a_{n+1}}{a_{n}}\) for n=1,2,3,4,5.
Answer:
Given a1 =1, a2=1,an = an-1 + an-2, n> 2

Arithmetic Progression (A.P.):
Question 1.
Define arithmetic progression. Answer : Let a1 ,a2, a3, be a sequence.
If a2 – a1 = a3 – a2 = a4 – a3 ………… i.e., the difference between any two consecutive terms is always same constant, then the sequence is called an Arithmetic progression (AP). The constant difference a2 – or a3 – a2 etc is called common difference and it is denoted by ‘d’.
![]()
Question 2.
Write the formulae for finding nth term and sum to first ‘n’ term of Arithmetic progression.
Answer :
The nth term of A.P.: If the first term of an A.P. is ’a1 ’ and the common difference is ‘d’,
then the nth an = a1 + (n -1 )d
Observation:
The A.P. with first term ‘a’ and common difference d’ is
a,a + d,a + 2d,a + 3d ……………….
Sum to first ‘n’ term of A.P.:
The sum to first ‘n’ terms of an A.P. with first term ‘a1‘ and common difference ‘d’ is,
\(S_{n}=\frac{n}{2}\left[2 a_{1}+(n-1) d\right] \text { or }\)
\(S_{n}=\frac{n}{2}\left[a_{1}+a_{n}\right]\)
Question 3.
Find the sum of odd integers from 1 to 2001.
Answer :
Required sum =1 + 3 + 5 +……….. + 2001
This series is in AP with a1 = 1, d = 2 (i.e., 3-1=2) and an =2001.

Question 4.
Find the sum of all natural numbers lying between 100 and 1000, which are multiples
of 5.
Answer :
Since 105, 110, 115,………… 995 are the numbers lying between 100 and 1000, are multiples of 5.
∴ Required sum =105 + 110+115 + ……………….+ 995.
This series in A.P. with an =105.
d = 110-105 = 5 and an= 995.
We have,
an = a, + (n -1 )d
⇒ 995 = 105 + (n -1)(5)
⇒ 995 = 105 + 5/1-5
⇒ 895 = 5n
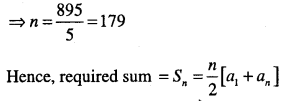

Question 5.
In an A.P, the first term is 2 and the sum of the first five terms is one- fourth of the sum
of next five terms. Show that 20th term is – 112.
Answer :

Question 6.
How many terms of A.P.\(-6, \frac{-11}{2},-5, \dots \dots \dots\) are needed to give the sum – 25?
Answer:

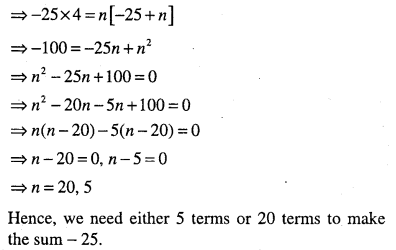
![]()
Question 7.
In an A.P., if pth term is \(\frac{1}{q}\) and qth term is \(\frac{1}{p}\),
prove that the sum of first pq terms is \(\frac{1}{2}(p q+1)\), where p≠q.
Answer :
Let ‘a’ be the first term and ‘d’ bet he common difference of an A.P. then, nth term


Question 8.
If the sum of a certain number of terms of the A.P 25,22,19,……… is 116. Find the last term.
Answer :
Let ‘a’ be the first term and ‘d’ be the common difference of an A.P. then

Question 9.
Find the sum of n terms of the A.P., whose kth term is 5A: +1
Answer :
Given kth term = 5k + 1
Substituting k = 1, 2, 3,……. , we get
1st term = 5(1)+ 1 = 6
2nd term = 5(2) + 1 = 11
3rd term = 5(3) + l = 16 etc.
Series in A.P. is 6 + 11 + 16 +………..
∴ Sum of first n terms
\(=S_{n}=\frac{n}{2}[2 a+(n-1) d]\)
\(\Rightarrow S_{n}=\frac{n}{2}[2(6)+(n-1)(5)]\)
\(=\frac{n}{2}[12+5 n-5]=\frac{n}{2}[7+5 n]=\frac{1}{2}\left[7 n+5 n^{2}\right]\)
Question 10.
If the sum of ‘n’ terms of an A.P. is (pn + qn2), where p and q are constant find the common difference.
Answer :
Given Sn= pn + qn2 ………………(1)
Substituting n = 1, 2, we get
S1= p(1) + q(1)2 = p + q and
S2 =p(2) + q(2)2 =2p + 4q
we know that, S1=a = first term and S2 = first term + second term = a + (a + d),
where d = C.D.
S2 = 2a + d
= 2p + 4q = 2 (p + q) + d = 2p + 2q + d
= d = 2p + 4q-2p-2q = 2q
![]()
Question 11.
The sums of nterms of two arithmetic progressions are in the ratio 5n + 4 : 9n+ 6, find the ratio of their 18th
Answer :


Question 12.
If the sum of first ‘p’ terms of an A.P. is equal to the sum of the first ‘q’ terms, then find the sum of the first (p +q) terms.
Answer:
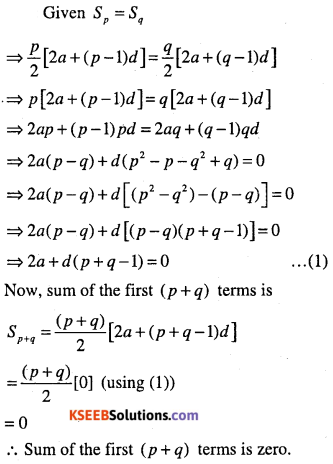
Question 13.
Sum of the first p, q and r term of an A.P. are a, b and c respectively. Prove that
\(\frac{a}{p}(q-r)+\frac{b}{q}(r-p)+\frac{c}{r}(p-q)=0\)
Answer:
Let A be the first term and D be the common ratio of an A.P.
Given, Sp=a, Sq=b and Sr=c

![]()
Question 14.
The ratio of the sums of m and n terms of an A.P. is m2: it2 .Show that the ratio of mth and nth term is (2m -1): (2n -1).
Answer :
Let ‘a’ be first term and ‘d’ be the common difference of an A.P. then,


Question 15.
If the sum of n terms of an A.P. is 3n2 + 5n and its mth term is 164, find the value of m.
Answer :
Given Sn =3n2 + 5n ………..(1)
and am = mth term = 164
⇒ 164 = a + (m – 1)d ………………… (2)
Substitute n = 1, 2 in (1), we get
S1= 3(1)2 + 5(1) = 3 + 5 = 8 and
S2 = 3(2)2 +5(2) = 12+ 10 = 22
We know that, S1 = first term = a and S2 = Sum of first two terms.
∴ S1= 8 = a and a + (a + d) = 22
∴ <3 = 8 and 8 + (8 + d) = 22
⇒ d = 6
Substituting the values of a and d in (2), we get 164 = 8 +(m-1)(6)
= 8 + 6m-6 = 2 + 6m
\(\Rightarrow 162=6 m \Rightarrow m=\frac{162}{6}=27\)
![]()
Question 16.
If \(\frac{a^{n}+b^{n}}{a^{n-1}+b^{n-1}}\) is the A.M between a and b then find the value of n; a ≠ b.
Answer:

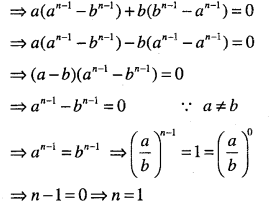
Question 17.
Insert five numbers between 8 and 26 such that the resulting sequence is an A.P.
Answer :
Let required five numbers be x1, x2, x3, x4, x5
∴ 8, x1, x2, x3, x4, x5, 26 are in A.P.
⇒ First term = 8 and seventh term
= 26 ⇒ a = 8 and a + 6d-26
⇒(3 = 8 and 6d = 26 – a = 26 – 8 = 18
⇒ a = 8 and d = 3
Hence
x1= a+d = 8 + 3 = 11
x2 = a + 2d = 8 + 6 = 14
x3 = 17, x4 = 20, x5 = 23
Question 18.
Between 1 and 31, ‘m’ numbers have been inserted in such a way that the ratio of 7th and (m – 1)th numbers is 5 : 9. Find the value of
Answer :

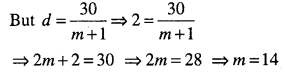
![]()
Question 19.
A man starts repaying a loan as first installment of Rs. 100. If he increases the installment by Rs. 5 every month, what amount he will pay in the 30th installment?
Answer :
By data, the installments paid by the man are
100, 105, 110, ……………… which is in A.P. with
a = 100 and d = 5
Hence 30th installment = 30th term
= a + 29d =100 + 29(5) =245
Question 20.
The difference between any two consecutive interior angles of a polygon is 5° (5 degree). If the smallest angle is 120°, find the number of the sides of polygon.
Answer :
Let the number of sides of the polygon be n, then the sum of all exterior angles = 360° and sum of all interior angles = 180° n – 360°.
Given, smallest angle = 120° and difference between the angles = 5°.
∴ Angles are of the form,

Geometric Progression (G.P.):
Question 1.
Define geometric progression.
Answer :
A sequence of non-zero terms is called a geometric progression if the ratio of any term to its preceding term is constant. This constant is called common ratio and is denoted by ‘r’
Question 2.
Write the general term of a G.P.
Answer :
Let a be the first term and r(≠0) be the common ratio of a G.P. Then general term of G.P. is
Tn = a . rn-1
Note:
- Terms in G.P. are in the form a, ar, ar2, arn-1,
- No term in G.P. can be zero.
- Three terms a,b,c are in G.P.
\(\text { iff } \frac{b}{a}=\frac{c}{b} \text { i.e. }b^{2}=a c, a b c \neq 0\)
![]()
Question 3.
Write the formula for finding the sum of n terms of a G.P.
Answer :
Let ‘a’ be the first term and ’r’(≠) be the common ratio of the given G.P. The general teams of G.P. If Sn denotes the sum of ‘n’ terms, then,
\(S_{n}=a\left(\frac{1-r^{n}}{1-r}\right) r \neq 1\)
This can also written as
\(S_{n}=a\left(\frac{r^{n}-1}{r-1}\right)\)
Note:
(1) Sn=a + ar + ar2+….. +arn-1
(2) If r = 1, then Sn = a + a + a +……………+a – na
(3) If r = 1, then formulas for Sn fail
(4) If r < 1, then use \([S_{n}=a\left(\frac{1-r^{n}}{1-r}\right)\)
(5) If r > 1, use \(S_{n}=a\left(\frac{r^{n}-1}{r-1}\right)\)
(6) Sum of an infinite G.P., a + ar + ar2 +……. is \(\frac{a}{1-r},-1<r<1\)
(7) If a, b, c are in G.P. then ‘b’ is the G.M. (geometric mean) between a and c, then b2 =ac – \(\Rightarrow b=\sqrt{a c}\)
(8) If A and G are A.M. and G.M. of two given distinct positive real numbers, then relation between A and G is A > G.
Question 4.
Find the 20th and nth terms of the G.P.:
\(\frac{5}{2}, \frac{5}{4}, \frac{5}{8}, \dots \dots .\)
Answer:

Question 5.
Find the 12th term of a G.P. whose 8th term is 192 and common ratio is 2
Answer:

![]()
Question 6.
The 5th, 8th and 11th terms of G.P. are p, q and s respectively. Show that q2 = ps
Answer:

Question 7.
The 4th term of a G.P. is square of its second term and the first term is – 3. Determine its 7th term.
Answer:
Let G.P. be a, ar, ar2,………….. , then
Tn=arn-1
Given: a = -3 and T4 =(T2)2
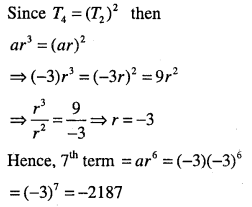
Question 8.
Which term of the sequence
(a) \(2,2 \sqrt{2}, 4, \cdots \cdots \text { is } 128 ?\)
(b) \(\sqrt{3}, 3,3 \sqrt{3}, \cdots \cdots \cdots \text { is } 729 ?\)
(c) \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \dots \dots \text { is } \frac{1}{19683} ?\)
Answer:

Question 9.
For given value of x, the number \(-\frac{2}{7}, x, \frac{-7}{2}\) are in G.P.?
Answer:
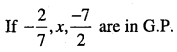
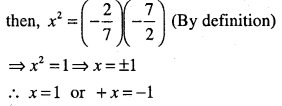
Question 10.
Find the sum of indicated terms in each of the following G.P.
(a) 15,0.015, 0.0015,……. 20 terms.
(b) \(\sqrt{7}, \sqrt{21}, 3 \sqrt{7}, \dots \dots n \text { terms. }\)
(c) 1,-a ,a2, -a3,……….. n terms (if a ≠ – 1)
(d) x3, x5, x7,………. n terms (x ≠ ± l)
Answer:

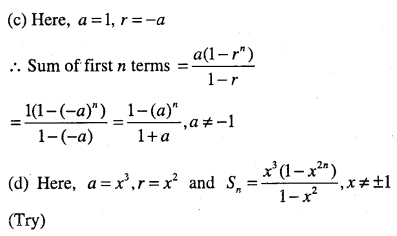
![]()
Question 11.
Evaulate:
\(\sum_{k=1}^{11}\left(2+3^{k}\right)\)
Answer:
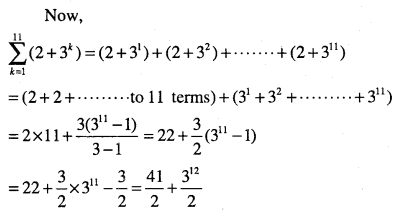
Question 12.
The sum of first three terms of a G.P. is \(\frac{39}{10} \) and their product is 1. Find the common ratio and the terms.
Answer:

Question 13.
How many terms of G.P. 3, 32, 33,34,……………… are needed to give the sun 120?
Answer :

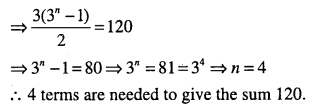
![]()
Question 14.
The sum of first three terms of a G.P. is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio and the sum to ‘n’ terms of the G.P.
Answer:
Let ‘a’ be the first term and V be the common ratio of the G.P. then a, ar, ar2,…… are in G.P.

Question 15.
Given a G.P. with a = 729 and 7th term 64, determine S7.
Answer :
Let ‘r’ be the common ratio.

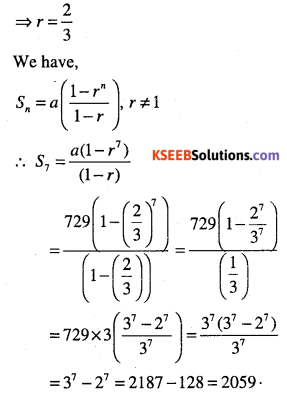
![]()
Question 16.
Find a G.P. for which sum of the first two terms is – 4 and fifth terms is 4 times the third term.
Answer :
Let ‘a’ bet the first term and V be the common ratio of a G.P.

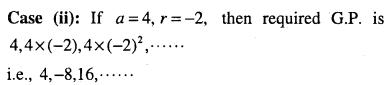
Question 17.
If the 4th, 10th and 16th terms of a G.P. are x, y and z respectively. Prove that x, y, z are in G.P
Answer:

![]()
Question 18.
Find the sum to ‘n’ terms of the sequence 8, 88,888, 8888,………
Answer :

Question 19.
Find the sum of the product of the corresponding terms of the sequences 2, 4, 8,
16,32 and 128,32, 8,2, \(\frac{1}{2}\)
Answer :
Given two sequences are, 2, 4, 8, 16, 32 and 128, 32, 8,2\(\frac{1}{2}\)
∴ Required sum = 2 x 128 + 4 x 32 + 8 x 8 + 16 x 2 + 32 x\(\frac{1}{2}\)

Question 20.
Show that the products of the corresponding terms of the sequences
a, ar, ar2 ,……….arn-1 and A, AR, AR2,……….. AR-1 form a G.P. and find the common ratio.
Answer :
Given sequences are, a, ar, ar2 ,……….arn-1……………….(1)
and A,AR,AR2,………. ,AR-1 ……………….(2)
Now, multiply the corresponding terms of equations (1) and (2), we get
aA, aArR, aAr2R2,….
i.e., (aA),(aA)(rR), (aA)(rR)2,..
which is in G.P. with common ratio rR.
![]()
Question 21.
Find four numbers forming a geometric progression in which the third term is greater than the first term by 9, and the second term is greater than the 4th term by 18.
Answer :
Let ‘a’ be the first term and ‘r’ be the common ratio of a G.P. .
Four numbers in G.P. be a,ar,ar2 and ar3
Given that T3 = Tx + 9 and T2=T4+18.
i.e., ar2-a + 9 …………….. (1) and
ar = ar3+18 ……………… (2)
From (1), we get
ar2 – a = 9
⇒ a(r2 -l) = 9 …(3)
From (2), we get
ar – ar3 =18
⇒ nr(1- r2) = 18 …(4)
Dividing (4) by (3), we get
r = 2 ⇒ r = -2
Substituting r = – 2 in (1), we get
a( 4) = a + 9
⇒ 3a = 9
⇒ a = 3 Hence, four numbers are,
⇒ 3, 3(-2), 3(-2)2, 3(-2)3 i.e., 3,-6,12,-24
Question 22.
If the first and nth term of a G.P. are a and b respectively, and if ‘P’ is the product of ‘n’ terms, prove that aq – r ,br – p ,cr – q = 1
Answer :
Let A and R be the first term and common ratio of a G.P. Then T=ARn-l.
Let A be the first term and R be the common ratio of a G.P.

![]()
Question 23.
If the first and nth term of a G.P. are a and b respectively, and if ‘P’ is the product of ‘n’ terms, prove that P2 = (ab)n
Answer :
Let A be the first term and R be the common ratio of a G.P.

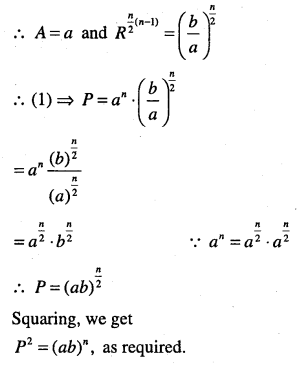
Question 24.
Show that the ratio of the sum of first ‘n’ terms of a G.P. to the sum of the terms from
\((n+1)^{\mathrm{th}} \text { to }(2 n)^{\mathrm{th}} \text { term is } \frac{1}{r^{n}}\)
Answer:
Let ‘a’ be the first term and ‘r’ be the common ratio of a G.P

![]()
Question 25.
If a, b, c, d are in G.P. show that (a2 + y2 +c2)(b2 +c2 +d2) = (ab + bc +cd)2
Answer:
Given a,b,c,d are in G.P.
Let a = a, b = ar, c = ar2 and d = ar3 and common ratio ‘r’.
LHS = (a2 +b2 +c2)(b2 +c2 +d2)
= (a2+a2r2 + a2r4)(a2r2 + a2r4 +a2r6)
= a2(1 + r2 + r4)a2(r2 +r4 + r6)
= aV(1 + r2 + r4)(l + r2 + r4)
= a4r2(1 + r2+ r4)2 ……………………(1)
RHS = (ab + bc + cd)2
= (a2r + a2r3 + a2r5)2
= [a2r(1 + r2 + r4)]2
= a4r2 (1 + r2 + r4)2 ……………………(2)
From (1) and (2)
Question 26.
Insert two numbers between 3 and 81 so that the resulting sequence is G.P.
Answer :
We b and c be the numbers between 3 and 81.
a-3, b = ar = 3r, c = ar2 = 3r2 and d = ar3 = 3r3 =T4
But T4 =ar4-1 = 3r3
⇒ 81 = 3r3
⇒ r3 = 27 = 33
⇒ r = 3
∴ b = ar = 3 x 3 = 9
and c = ar2 =3 x 32 = 27
![]()
Question 27.
Find the value of ‘n’so that\(\frac{a^{n+1}+b^{n+1}}{a^{n}+b^{n}}\) may a +b be the geometric mean between a and b.
Answer :

Question 28.
The sum of two numbers is 6 times their geometric mean, show that the numbers are in the ratio \((3+2 \sqrt{2}):(3-2 \sqrt{2})\)
Answer:
Let the number be a and b
Where a>b>0 the given
\(a+b=6 \sqrt{a b} \Rightarrow a+b=3(2 \sqrt{a b})\)

![]()
Question 29.
If A and B be AM and GM respectively between two positive numbers, prove that the numbers are \(A \pm \sqrt{(A+G)(A-G)}\)
Answer:

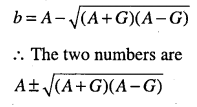
Question 30.
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour?
Answer :
Number of bacterias increasing in each hour is given by
30 x 2 x 30 x 22,30 x 23,30 x 24…….. is in G.P.
Number of bacteria present at the end of,
2nd hour = 30 x 22 = 120
4th hour = 30 x 24 = 30 x 16 = 480 and nth hour = 30 x 2n
Question 31.
What will Rs. 500 amounts to in 10 years after its deposit in a bank which pays annual interest rate of 10% compounded annually?
Answer :
Given the rate of interest is 10% compound annually.
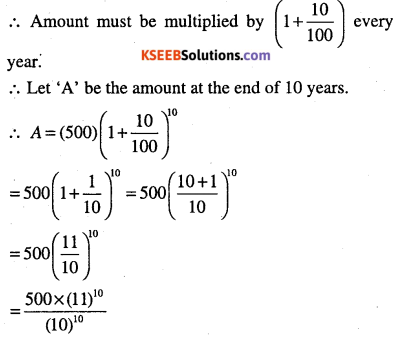
Question 32.
If AM and GM of roots of a quadratic equation are 8 and 5 respectively, then obtain the quadratic equation.
Answer:
Let m and n be the roots, then
\(\frac{m+n}{2}=A M=8 \Rightarrow m+n=16 \text { and } \sqrt{m n}=G M=5\)
Required quadratic equation is
⇒ x2 – (sum of the roots)x + product of the roots = 0
⇒ x2 -16 x + 25 = 0
Sum to ‘n’ terms of special series
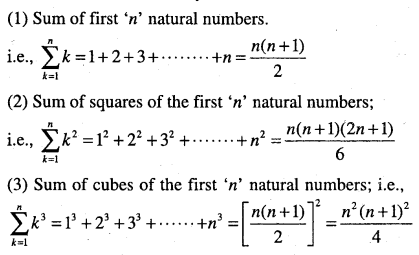
Exercise 9.4
I. Find the sum to ‘n’ terms of each of the series.
Question 1.
1 x 2 + 2 x 3 + 3 x 4 + 4 x 5 +………….
Answer:

![]()
Question 2.
1 x 2 x 3 x +2 x 3 x 4 x 3 x 4 x 5+…………….
Answer:

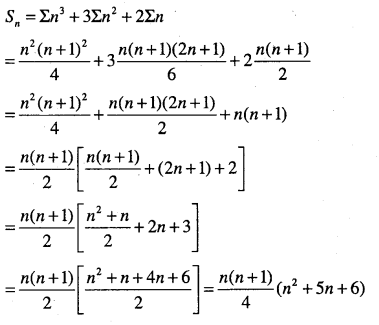
Question 3.
\(3 \times 1^{2}+5 \times 2^{2}+7 \times 3^{2}+\cdots \cdots\)
Answer:

Question 4.
\(\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\frac{1}{3 \times 4}+\dots+\dots\)
Answer:
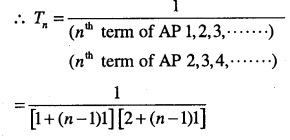
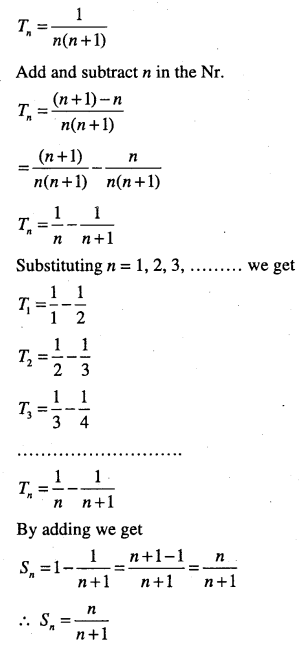
Question 5.
\(5^{2}+6^{2}+7^{2}+\cdots \cdots \cdots+20^{2}\)
Answer:

![]()
Question 6.
3 x 8+6 x 11 + 9 x 14+……………
Answer:
Tn denote the nth term of series.
Tn = (nth term of AP 3, 6, 9……… ) (nth term of AP 8,11,14………. )

Question 7.
\(\begin{aligned}&1^{2}+\left(1^{2}+2^{2}\right)+\left(1^{2}+2^{2}+3^{2}\right)+\cdots \cdots\\&+\left(1^{2}+2^{2}+3^{2}+\cdots \cdots+n^{2}\right)\end{aligned}\)
Answer:

![]()
II. Find the sum to ‘n’ terms of the series, whose nth term is given by
Question 8.
n(n +1)(n + 4)
Answer:

Question 9.
n2+2n
Answer:
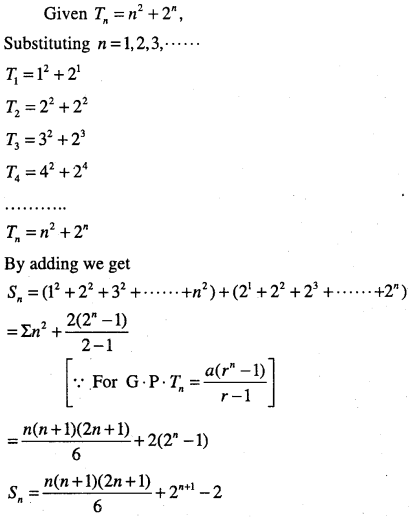
Question 10.
(2n-1)2
Answer:

Miscellaneous Exercise :
Question 1.
Show that the sum of (m + nth) and (m – n)th terms of an A.P. is equal to twice the mth
Answer :
Let ‘a’ be the first term and ‘d’ bet he common difference.

![]()
Question 2.
If the sum of three numbers in A.P. be 24 and their product is 440. Find the numbers.
Answer :
Let the three numbers be, a-d,a,a + d
Given (a-d) + a + (a + d) = 24
⇒ 3a = 24 ⇒ a = 8

Question 3.
Let the sum of n, 2n, 3n terms of an A.P. be S1, S2 and S3 respectively, show that S3=3(S2-S2)
Answer :
Let ‘a’ be the first term of d be the common difference of A.P.

Question 4.
Find the sum of all numbers between 200 and 400 which are divisible by 7.
Answer :
The numbers between 200 and 400 which are divisible by 7 are, 203, 210, 217,…… 399.
Required sum = 203 + 217 +…….. + 399
⇒ a = 203 and Tn = 399
⇒ 399 = 203 + (n -1)7 [∵ Tn = a + (n -1)d]
⇒ 399 = 203 + 7n-7
⇒7n = 399-203 + 7

![]()
Question 5.
Find the sum of integers from 1 to 100 that are divisible by 2 or 5.
Answer :
The integers from 1 to 100 that are divisible by
2 or 5 are 2, 4, 5, 6, 8…….. 90, 92, 94, 95, 96, 98, 100

Question 6.
Find the sum of all two digit numbers which when divided by 4, yields 1 as remainder.
Answer :
Two digit numbers which when divided by 4, yields 1 as remainder are
13,17, 21,…….. , 97.
∴ Required sum = 13 + 17 + 21 +…….. + 97.
⇒ which is an A.P.
a = 13,d =4,Tn =97
∴ Tn=a + (n- 1)d
97 = 13 + (n-1)4
⇒ 4n = 97-13 + 4 88
\(\Rightarrow n=\frac{88}{4}=22\)
\(\ S_{n}=\frac{22}{2}(13+97) \quad\left[\ S_{n}=\frac{n}{2}(a+l)\right]\)
\(S_{n}=11(110)=1210\)
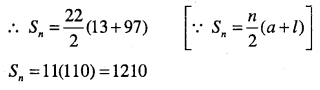
![]()
Question 7.
If f is a function satisfying
f(x + y) = f(x) f(y) ∀ x, y ∈ N such that f (1)
\(3 \text { and } \sum_{x=1}^{n} f(x)=120\),find the value of n.
Answer:

Question 8.
The sum of some terms of G.P is 315. Whose first term and the common ratio are 5 and 2, respectively. Find the last term and the number of terms.
Answer:
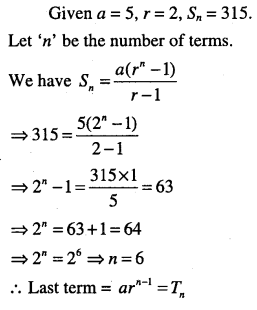
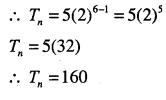
![]()
Question 9.
The first term of a G.P. is 1. The sum of the third and fifth terms is 90. Find the common ratio of G.P.
Answer:
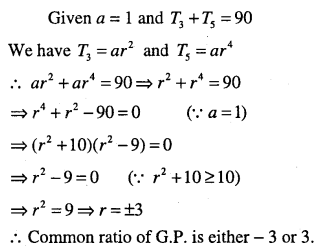
Question 10.
The sum of three numbers in G.P. is 56. If we subtract 1, 7, 21 from these numbers in that order, we obtain an A.P. Find the numbers.
Answer:
Let the three numbers G.P. be a, ar, ar2

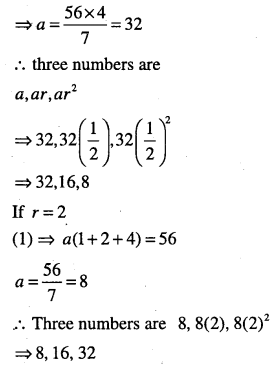
Question 11.
A G.P. consists of an even numbers of terms. If the sum of all the terms is 5 times the sum of terms occupying odd places, then find its common ratio.
Answer:
Let number of terms be 2n ,an even number.
∴ G.P, be a, ar, ar2 ar3,……… ar2n-2,ar2n-1

Question 12.
The sum of the first four terms of an A.P. is 56. The sum of the last four terms is 112. If its first term is 11. Then find the number of terms.
Answer:
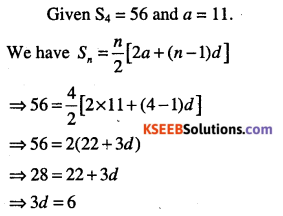
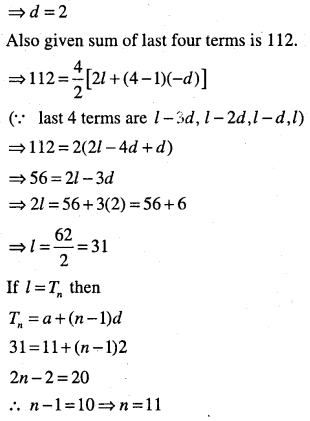
![]()
Question 13.
\(\text { If } \frac{a+b x}{a-b x}=\frac{b+c x}{b-c x}=\frac{c+d x}{c-d x}(x \neq 0)\) then show that a,b,c and d are in G.P
Answer:
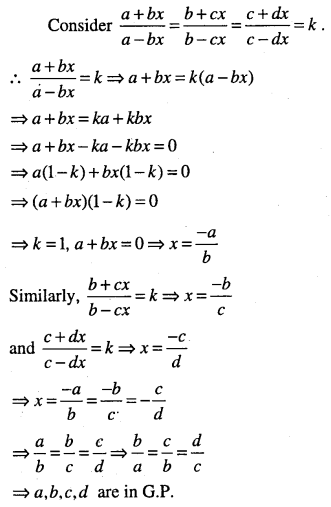
Question 14.
Let S be the sum, P be the product and R, the sum of reciprocals of ‘n’ terms in a G.P. prove that P2 Rn = Sn.
Answer :
Let ‘a’ be the first term and V be the common ratio of G.P

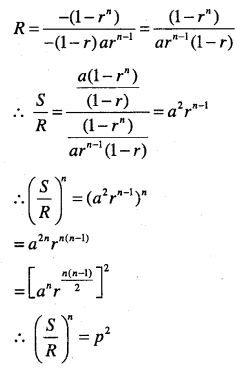
Question 15.
The pth, qth and rth terms of an A.P are a, b,c respectively . Show that
(q – r) a+(r – p)b+(p -q) c = 0
Answer:
Let A,A + D,A + 2D,…….. are in A.P.
Given pth term =A + (p – 1 )D = a ……………. (1)
qth term = A + (q – 1)D = b …………………. (2)
and rth term = A + (r-1)D = C …………………(3)
X (q- r) ⇒ a(q – r) = (q – r) [A + (p – 1)D]
X (r – p) ⇒ b(r-p) = (r-p)[A + (q – 1)D]
x(p-q) ⇒ c(p-q) = (p-q)[A + (r – 1)D]
By adding we get
⇒ a(q -r) + b(r – p) + c(p – q)
= A[(q-r) + (r-p) + (p-q) + D]
[(p -1 )(q – r) + (q – 1 )(r – p) + (r -1 )(p – q)]
= A(0) + D(0)
= 0
Question 16.
If \(a\left(\frac{1}{b}+\frac{1}{c}\right), b\left(\frac{1}{c}+\frac{1}{a}\right), c\left(\frac{1}{a}+\frac{1}{b}\right)\) are in A.P
Answer:

Question 17.
If a, b, c, d are in G.P. prove that (an + bn), (bn + cn), (cn + dn) are in G.P.
Answer:
Given a,b,c,d are in G.P.
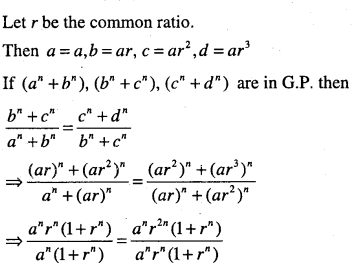
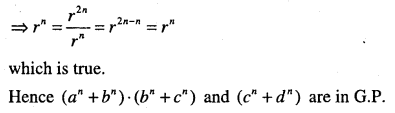
![]()
Question 18.
If a and b are the roots of x2 – 3x + p = 0 and c and d are roots of x2 – 12x + q = 0.
Where a, b, c, d form a G.P. prove that (q + p) : (q-p) = 17 : 15
Answer:

Question 19.
The ratio of the AM and GM of two positive numbers a and b is m : n. Show that
\( a: b=(m+\sqrt{m^{2}-n^{2}}):(m-\sqrt{m^{2}-n^{2}})\)
Answer:
We have \(A M=\frac{a+b}{2}\) and \(G M=\sqrt{a b}\)
Given Am : GM = m : n

Question 20.
If a, b, c are in A.P. b, c, d are in G.P. and \(\frac{1}{c}, \frac{1}{d}, \frac{1}{e}\)
are in A.P .Prove that a,c,e are in G.P.
Answer

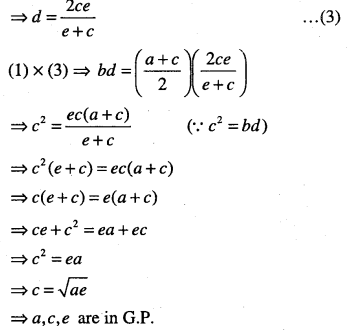
![]()
Question 21.
Find the sum of the following series upto n terms.
(1) 5 + 55 + 555 +……….
(2) 0.6 + 0.66 + 0.666 +……………….
Answer:

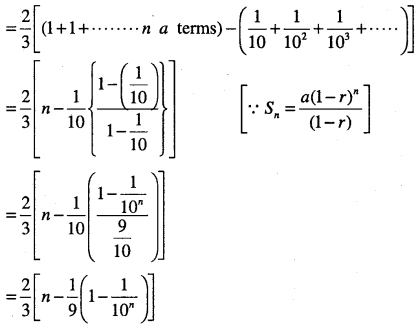
Question 22.
Find the 20th term of the series 2 x 4 + 4 x 6 +6 x 8+……….. + n terms.
Answer :
We have Tn = a + (n – 1)d
20th term of series
= [20th term of 2,4, 6….] x [20th term of 4, 6, 8….. ]
= [2 + (20 -1)2] x [4+ (20-1)2]
= (2+ 38)(4 + 38)
= (40)(42)
= 1680
Question 23.
Find the sum of the first ‘n’ terms of the series, 3 + 7 + 13 + 21 + 31 +…………
Answer :
Let Tn= nth term of the series and Sn = Sum of first ‘n’

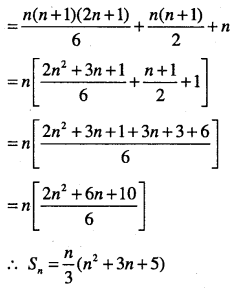
![]()
Question 24.
If S1, S2, S3 are the sum of first ‘n’ natural numbers, their squares and their cubes, respectively, show that 9S2 = S3(1+ 8S1)
Answer:

Question 25.
Find the sum of the following series up to n term
\(\frac{1^{3}}{1}+\frac{1^{3}+2^{3}}{1+3}+\frac{1^{3}+2^{3}+3^{3}}{1+3+5}+\cdots\)
Answer:
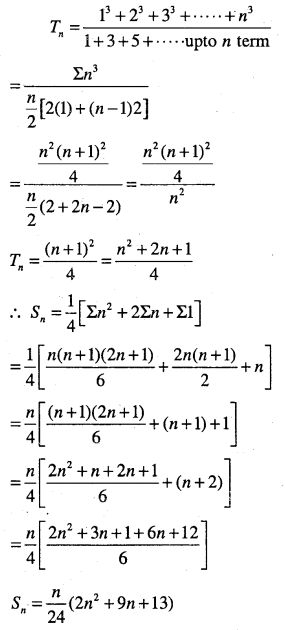
![]()
Question 26.
Show that
\(\frac{1 \times 2^{2}+2 \times 3^{2}+\cdots+n(n+1)^{2}}{1^{2}+2+2^{2} \times 3+\cdots+n^{2}(n+1)}=\frac{3 n+5}{3 n+1}\)
Answer:
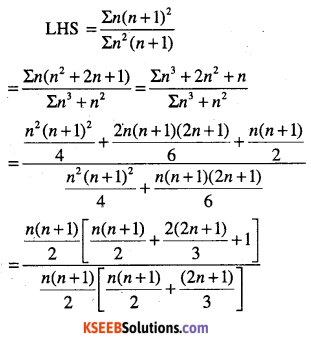
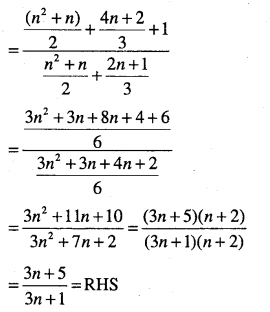
Question 27.
A farmer buys a used tractor for Rs. 12,000. He pays Rs. 6000 cash and agrees to pay the balance in annual instalments of Rs. 500 plus 12% interest on the unpaid amount. How much will the tractor cash him?
Answer:

![]()
Question 28.
Shamshad Ali buys a scooter for Rs. 22000. He pays Rs. 4000 cash and agrees to pay the balance in annual installment of Rs. 1000 plus 10% interest on the unpaid amount. How much will the scooter cost him?
Answer :

Question 29.
A person writes a letter to four of his friends. He asks each one of them to copy the letter and mail to four different persons with instruction that they move the chain similarly. Assuming that the chain is not broken and that it costs 50 paise to mail one letter. Find the amount spent on the postage when 8th set of letter is mailed.
Answer :

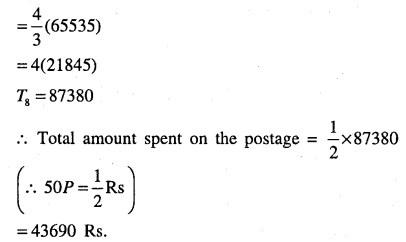
Question 30.
A man deposited Rs. 10,000 in a bank at the rate of 5% simple interest annually. Find the amount in 15th year since he deposited the amount and also calculate the total amount after 20 years.
Answer:

Question 31.
A manufacturer reckons that the value of a machine, which costs him Rs. 15625, will depreciate each year by 20%. Find the estimated value at the end of 5 years.
Answer:
Cost of the machine at the end of one year [larex]5625\left(1-\frac{20}{100}\right)[/latex]
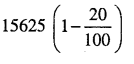
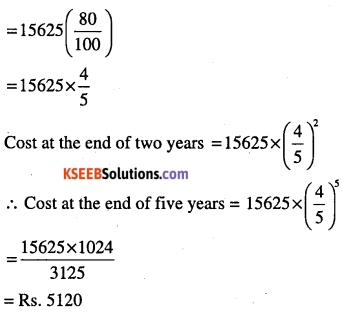
![]()
Question 32.
150 workers were engaged to finish a job in a certain number of days. 4 workers dropped out on second day, 4 more workers dropped out on third day and so on. It took 8 more days to finish the work. Find the number of days in which the work was completed.
Answer :
Let V be the number of days that the work was to be completed
∴ For one worker, number of days required to complete the work = 150 n.
150 + 146 + 142 + ….upto (n + 8) terms = 150 n.