Students can Download Maths Chapter 3 Matrices Miscellaneous Exercise Questions and Answers, Notes Pdf, 2nd PUC Maths Question Bank with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Maths Question Bank Chapter 3 Matrices Miscellaneous Exercise
Question 1.
Let \(A=\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}\), Show that (al +bA)n + nan – 1 ba where 1 is the identity matrix of order 2 and n ∈ N.
Answer:

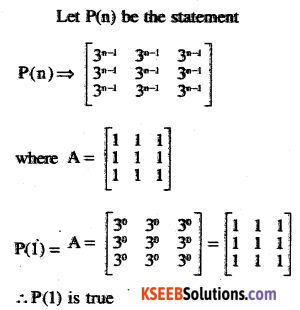
Question 2.
If\(A=\left[\begin{array}{lll}{1} & {1} & {1} \\{1} & {1} & {1} \\{1} & {1} & {1}\end{array}\right]\)
,prove that
An = \(\left[\begin{array}{lll}{3^{n-1}} & {3^{n-1}} & {3^{n-1}} \\{3^{n-1}} & {3^{n-1}} & {3^{-1}} \\{3^{n-1}} & {3^{n-1}} & {3^{n-1}}\end{array}\right], n \in N\)
Answer:

![]()
Question 3.
\(\mathbf{A}=\left[\begin{array}{ll}{\mathbf{3}} & {-4} \\{\mathbf{1}} & {\mathbf{1}}\end{array}\right]\)
then prove that
An = \(\left[\begin{array}{cc}{1+2 n} & {-4 n} \\{n} & {1-2 n}\end{array}\right]\) where n is any positive integer.
Answer:

∴ P (k +1) is true
P(n) is true for all the values of +ve n.
Question 4.
If A and B are symmetric matrices, prove that AB – BA is a skew symmetric matrix.
Answer:
Since A &B are symmetric matrices A = a’ & B = B’
To prove (AB – BA)’ = – (AB – BA)
L.H.S = (AB – BA)’
(AB)’ – (BA)’
= B’A’-A’B’
= BA – AB
= – (AB – BA) = R.H.S
Thus proved.
![]()
Question 5.
Show that the matrix g’AB is symmetric or skew symmetric according as A is symmetric or skew symmetric.
Answer:

Question 6.
find the values of x, y, z if the matrix
A = \(\left[\begin{array}{rrr}{0} & {2 y} & {x} \\{x} & {y} & {-z} \\{x} & {-y} & {z}\end{array}\right]\) satisfy the equation A’ A = 1
Answer:

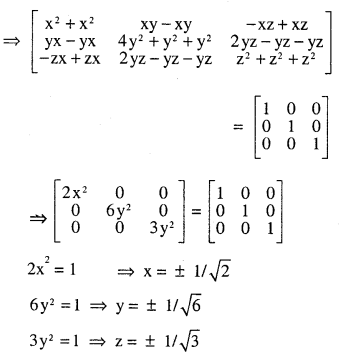
Question 7.
For what values of x:
\(\left[\begin{array}{lll}{1} & {2} & {1}\end{array}\right]\left[\begin{array}{rrr}{1} & {2} & {0} \\{2} & {0} & {1} \\{1} & {0} & {2}\end{array}\right]\left[\begin{array}{l}{0} \\{2} \\{x}\end{array}\right]=0 ?\)
Answer:

![]()
Question 8.
\(\mathbf{A}=\left[\begin{array}{rr}{3} & {1} \\{-1} & {2}\end{array}\right]\) show that A2 – 5A + 7I = 0
Answer:
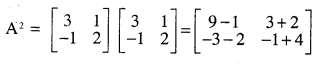

Question 9.
Find x, if
\(\left[\begin{array}{ccc}{\mathbf{x}} & {-5} & {-1}\end{array}\right]\left[\begin{array}{ccc}{\mathbf{1}} & {\mathbf{0}} & {\mathbf{2}} \\{\mathbf{0}} & {\mathbf{2}} &{\mathbf{1}} \\{\mathbf{2}} & {\mathbf{0}} &{\mathbf{3}}\end{array}\right]\left[\begin{array}{l}{\mathbf{x}} \\{\mathbf{4}} \\ {\mathbf{1}}\end{array}\right]=\mathbf{0}\)
Answer:
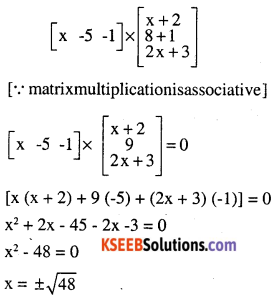
![]()
Question 10.
A manufacturer produces three products x, y, z which he sells in two markets. Annual sales are indicated below:

(a) If unit sale prices of, y and z are ₹2. 50, ₹1.50 and ₹1.00, respectively, find the total revenue in each market with the help of matrix algebra.
(b) If the costs of the above three commodities are ₹ 2.00, ₹ 1.00 and 50 paise respectively. Find the gross profit.
Answer:
Matrix representing the sales is

Profit in market I is
₹ 46,000 – ₹ 31,000
= ₹ 15,000
Profit in market 11 is
₹ 53,000 – ₹36,000
= ₹ 17,000
Gross profit
= ₹ 15,000 + ₹17,000
= ₹ 32,000.
Question 11.
Find the matrix X so that
\(\mathbf{X}\left[\begin{array}{lll}{1} & {2} & {3} \\{4} & {5} & {6}\end{array}\right]_{2 \times 3}=\left[\begin{array}{rrr}{-7} & {-8} & {-9} \\{2} & {4} & {6}\end{array}\right]_{2 \times 3}\)
Answer:

![]()
Question 12.
If A and B are square matrices of the same order such that AB = BA, then prove by induction that ABn = BnA. Further, prove that (AB)n = An Bn for all n ∈ N.
Answer:
(i) Let P(n) be the statement
P(n) – ⇒ Ab n = BnA
P(1) ⇒ AB = BA
∴ P( 1) is true
Let P(k) be true
P(k) ⇒ ABk = BkA
P(k +1) ⇒ ABk+1
= A(BkB) = (ABk)B
∵ matrix multiplication is associative.
⇒ (BkA) B ⇒ Bk (AB) = Bk (BA)
= (BkB) A = Bk+1 A
Hence P(k + 1) is true.
∴ P(n) is true for all the values of n ∈ N
(ii) Let P(n) be the statement
P(n) ⇒ (AB)n = AnBn
P(1) = (AB)1 = AB
∴ P(1) is true Let P(k) be true
P(k) ⇒ (AB)k
= AkBk P(k+1)
⇒ (AB)k+1 = (AB)kAB = (AkBk) AB
= Ak (BkA)B = Ak (ABk) B
(∵ ABn = BnA whenever Ab = BA)
= Ak+1 Bk+1
∴ P (k+1) is true
Hence P(n) is true for all the natures of n ∈ N
Choose correct answer in the following questions:
Question 13.
If \(\mathbf{A}=\left[\begin{array}{ll}{\alpha} & {\beta} \\{\gamma} & {-\alpha}\end{array}\right]\)
is such that A2= I ,then
(A) \(1+\alpha^{2}+\beta \gamma=0\)
(B) \(1-\alpha^{2}+\beta \gamma=0\)
(C) \(1-\alpha^{2}-\beta \gamma=0\)
(D) \(1+\alpha^{2}-\beta \gamma=0\)
Answer:
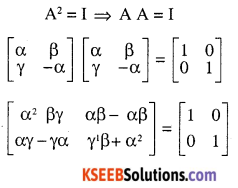
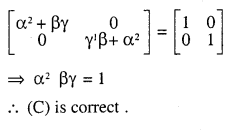
![]()
Question 14.
If the matrix A is both symmetric and skew symmetric, then
(A) A is a diagonal martix
(B) A is a zero matrix
(C) A is a square matrix
(D) None of these
Answer:
Let A be a square matrix such that A is both symmetric & skew-symmetric
⇒ A’ = A – (i) & A’ = – A -(ii)
⇒ A + A = 0 from (i) & (ii)
2A = 0
⇒ A = o
∴ (b) is correct
Question 15.
If A is square matrix such that A2 = A, then (I + A)3 – 7A is equal to
(A) A
(B) I – A
(C) I
(D) 3A
Answer:
A2 = A
(I + A)3 – 7A = (I + A) (I+A)2 – 7A
= (I + A) {(I + A) (I+A)} -7A
= (I + A) (I2 + 2A+A2) – 7A
[v IA = AI = A]
= (I + A) (I+2A+A) – 7A (A2= A)
= (I + A) (I + 3A) – 7A
= I2 + AI + 3IA + 3A2 – 7A
= I + A + 3A + 3A – 7A
[∵ A2 = A & IA = AI = A]
=1
∴ (C) is correct.
2nd PUC Maths Matrices Miscellaneous Exercise Additional Questions and Answers
One Mark Questions:
Question 1.
If \(\mathbf{A}=\left(\begin{array}{ll}{\mathbf{0}} & {\mathbf{1}} \\{\mathbf{1}} & {\mathbf{0}}\end{array}\right), \mathbf{F} \text { ind } \mathbf{A}^{4}\)
(UP CET 2010)
Answer:

Question 2.
If
\(\mathbf{A}=\left(\begin{array}{rr}{0} & {2} \\{3} & {-4}\end{array}\right), \mathbf{K A}=\left(\begin{array}{ll}{0} & {3 \mathbf{a}} \\{2 \mathbf{b}} & {24}\end{array}\right)\),find k, a and b.
Answer

![]()
Question 3.
Find X and Y
\(2 \mathbf{X}-\mathbf{Y}=\left[\begin{array}{rrr}{6} & {-6} & {0} \\{-4} & {2} & {1} \end{array}\right]\)
\(\mathbf{X}+2 \mathbf{Y}=\left[\begin{array}{rrr}{3} & {2} & {5} \\{-2} & {1} & {-7}\end{array}\right]\)
Answer:
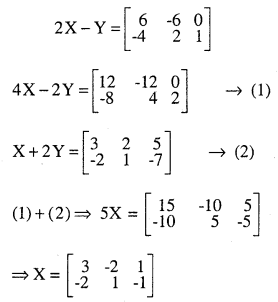

Question 4.
\(\left[\begin{array}{rrr}{1} & {1} & {1} \\{1} & {-2} & {-2} \\{1} & {3} &{2}\end{array}\right]\left[\begin{array}{l}{x} \\{y} \\{z}\end{array}\right]=\left[\begin{array}{l}{0} \\{3} \\{4}\end{array}\right], \text { then }\left[\begin{array}{l}{x} \\{y} \\{z}\end{array}\right]\)(I I T 2006)
Answer:
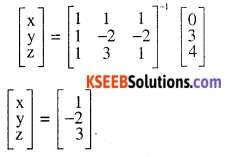
Question 5.
\(\mathbf{A}=\left[\begin{array}{lll}{6} & {8} & {7} \\{4} & {2} & {3} \\{9} & {7} & {1}\end{array}\right]\)
is the sum of symmentric and skew symmentric matrix, Find B
Answer:
