Students can Download 2nd PUC Physics Model Question Paper 3 with Answers, Karnataka 2nd PUC Physics Model Question Papers with Answers helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.
Karnataka 2nd PUC Physics Model Question Paper 3 with Answers
Time: 3 Hrs 15 Min
Max. Marks: 70
General Instructions:
- All parts are compulsory.
- Answers without relevant diagram/figure/circuit wherever necessary will not cany any marks
- Direct answers to the Numerical problems without detailed solutions will not carry any marks.
Part – A
I. Answer all the following questions ( 10 × 1 = 10 )
Question 1.
What is an equipotential surface?
Answer:
An equipotential surface is a surface with a constant value of potential at all points on the surface.
Question 2.
Define ‘drift velocity’ of free electrons.
Answer:
It is defined as the average velocity with which free electrons get drifted towards the positive end of a conductor (opposite to the electric field) under the influence of an external electric field.
Question 3.
Give an application of cyclotron.
- It is used to accelerate positively charged particles to very high energies.
- It is used to produce radioaactive material for medical purpose ex; for the purpose ex; for the purpose of diagnostics and treatment of chronic disease.
- It is used to synthesize fresh materials.
- It is used to improve the quality of solids by adding ions.
- It is used to bombard the atomic nuclei with highly accelerated particles to stydy the nuclear reactions.
Question 4.
State Faraday’s law of electro magnetic induction.
Answer:
The magnitude of induced emf is directly proportional to the rate of change of magnetic flux lined with the coil.
Question 5.
If the peak value of a.c. current is 4.24 A, what is its root mean square value?
Answer:
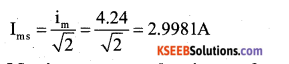
![]()
Question 6.
Mention one power loss in the transformer.
Answer:
Loss due to heating.
Loss due to flux linkage.
Loss due to eddy currents.
Hysteresis loss.
Question 7.
Two lenses of power + 1.5D and -0.5D are kept in contact on their principal axis. What is the effective power of the combination?
Answer:
P = P1 + P2= +1.5 – 0.5 = +1D
Question 8.
The decay of proton to neutron is possible only inside the nucleus. Why?
Answer:
Proton has smaller mass than a neutron.
Question 9.
What is ‘depletion region’ in a semiconductor diode?
Answer:
The space-charge region on either side of the junction (where there is a reduction/ decrease/depletion of mobile charge carriers) is called depletion region.
Question 10.
What is the output of the combination?
Answer:
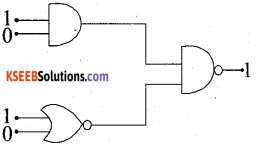
Part – B
II. Answer any five of the following questions. ( 5 × 2 = 10 )
Question 11.
Mention any two factors on which the capacitance of a parallel plate capacitor depends.
Answer:
The capacitance of a parallel plate capacitor depends on area of each place, dielectric medium between the plates and distance between the plates.
Question 12.
State Kirchofls laws of electrical network
Answer:
Kirchoff’s current law: The algebraic sum of currents entering the leaving a node of an electrical network is zero.
Kirchhoff’s voltage law: The algebraic sum of ‘IR’ products is equal to the algebraic sum of emfs, in that mesh of an electrical network.
![]()
Question 13.
Define magnetic ‘declination’ and ‘dip’ at a place.’
Answer:
Magnetic Declination (θ): The angle between the magnetic meridian and geographic meridian at a place is called Magnetic Declination at that place.
Magnetic Inclination or angle of dip (I): It is the angle between the direction of total magnetic field of earth and a horizontal line in magnetic meridian.
Question 14.
Write the expression for magnetic potential energy of a magnetic dipole kept in a uniform magnetic field and explain the terms.
Answer:
U = \(\overrightarrow{\mathrm{m}} \cdot \overrightarrow{\mathrm{B}}\) or U = m Bcosθ
U – Magnetic potential energy, m – magnetic moment of the magnetic dipole.
B – Uniform magnetic field.
Question 15.
Give any two applications of X-rays.
Answer:
X-rays are used
- as a diagnostic tool in medicine to detect freacture of bones, foreign bodies like bullets and stones in body.
- in the treatment of certain cancer.
- for detecting faults, cracks and flaws in metal casting.
- in the investigation of structure of crystals.
- to cause photoelectric effect.
Question 16.
What is ‘myopia’? How to rectify it?
Answer:
Myopi: It is a defect of human eye which can see near objects clearly but cannot see the far objects clearly. It can be corrected by using a concave lens of suitable focal length.
Question 17.
Draw the diagram representing the schematic arrangement of Geiger- Marsdon experimental set up tor the alpha particle scattering.
Answer:
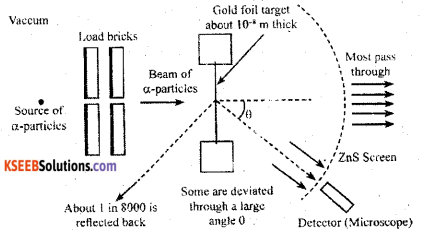
Question 18.
Write any two characteristics of nuclear force.
Answer:
Characteristics of Nuclear force.
- It is the strongest force in nature
- It is spin dependent.
- It is a short range force.
- It is exchange force.
- It is charge independent.
- Nuclear force has the property of Saturation.
- It is a noncentral force.
part – C
III. Answer any five of the following questions. ( 5 × 3 = 15 )
Question 19.
Give three properties of electric charge.
Answer:
Additivity of charges, Conservation of charges, Quantization of charge.
![]()
Question 20.
State Ampere’s circuital law and arrive at the expression for magnetic field near a straight Infinite current carryi ng wire.
Answer:
The line intergral of \(\overrightarrow{\mathrm{B}} \cdot \mathrm{d} \overrightarrow{\mathrm{l}}\) around any closed path enclosing a surface is times the total steady current passing through the surface. Consider a straight conductor of infinite length in the plane of the paper. Let I be the current through it from X to Y. Let P be a point at a perpendicular distance r from the straight wire. Consider a circle of radius r around the wire passing through P as an amperian loop. The magnetic field \(\overrightarrow{\mathrm{B}}\) at P due to the current in wire is tangential to the circle. Hence the magnetic field \(d \vec{l}\) is parallel to the line element at P.

Question 21.
What is hysteresis? Define the terms ‘coercivity’ and ‘retentivity’ of a ferro magnetic material.
Hysteresis :
The phenomenon of lagging behind the magnetic induction ( \(\overrightarrow{\mathrm{B}}\) ) with respect to the magnetizing field (\(\overrightarrow{\mathrm{h}}\) ) is called hysteresis.
Retentivity :
The property of the magnetic material to retain magnetism even in the absence of the magnetizing field is known as retentivity or remanence.
Coercivity :
The magnetizing field (H) needed to demagnetize the magnetic material completely is known as coercivity.
Question 22.
Arrive at Snell’s law of refraction, using Huygen’s principle for refraction Using Huygens principle for refraction of a plane wave.
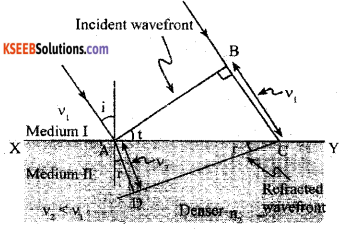
Answer:
Let XY represent the surface separating the medium-I and medium – II. Let V1 and V2 be the speed of light in medium -1 and medium- II respectively. Consider a plane wave front AB incident in medium-I at an angle i. Let the secondary wavelet from B strike the surface XY at C in a time t, then BC = V1t Secondary wavelet from A will travel a distance V2t as radius draw an arc in the medium II. The tangent from C touches the arc at D.
Let r be the angle of refraction.

If c represents the speed of light in vacuum then,

This is the Snell’s law of refraction.
Question 23.
Write Bohr’s postulates for the hydrogen atom model.
Answer:
First Postulate: Electron revolves round the nucleus in discrete circular orbits called stationary orbits without emission of radiant energy. These orbits are called stable orbits or non-radiating orbits.
Second Postulate : Electrons revolve around nucleus only in such orbits for which the angular momentum is some integral multiple of (h/2 π).
Third Postulate : When an electron makes a transition from one of its non-radiating orbits of another of lower energy, a photon is emitted having energy equal to the energy difference between the two state. The frequency of the emitted photon is the given by, hv = Ei – Ef
![]()
Question 24.
Derive the expression for the half-life of a radio active nuclide.
Answer:
At time t the number of atoms present in a radioactive sample is.

Question 25.
Write any three distinctions between p-type and n-type semi conductor. n-type semiconductor
Answer:
- Obtained by doping pentavalent impurity to a pure semiconductor.
- Majority charge carriers are free electrons.
- Minority charge carriers are holes
- At OK only free electrons are available for conduction.
- Donor energy level is slightly below the bottom of conduction band.
- Impurity atom is called donor impurity. p-type semiconductor
- Obtained by doping trivalent impurity to a pure semiconductor.
- Majority charge carriers are holes.
- Minority charge carriers are free electrons.
- At OK only holes are conduction.
- Acceptor energy level is slightly above the top of valance band.
- impurity atom is called acceptor impurity.
p-type semiconductor
- Obtained by doping trivalent impurity to a pure semiconductor.
- Majority charge carriers are holes.
- Minority charge carriers are free electrons. At OK only holes are conduction.
- Acceptor energy level is slightly above the top of valance band.
- impurity atom is called acceptor impurity.
![]()
Question 26.
Draw the block diagram of generalised communication system.
Answer:
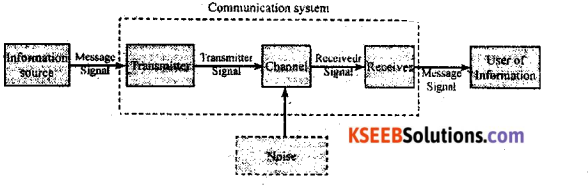
Part – D
IV. Answer any two of the following questions ( 2 × 5 = 10 )
Question 27.
Define electric potential due to a point charge and arrive at the expression for the electric potential at a point due to a point charge.
Answer:
The electrostatic potential at any point in an electrostatic field is defined as the work done in carrying a unit positive charge from infinity to that point against the electrostatic force of the field.
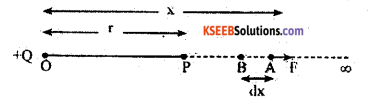
Consider a point Charge +Q at O
Let P be a point at a distance r from O
Consider a point A at a distance x from O.
The magnitude of electrostatic force positive charge at A is,
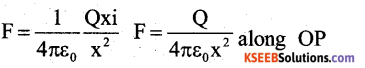
Work done in moving a unit positive charge from A to B though a small distance dx is, \(\Delta \mathrm{W}=\overrightarrow{\mathrm{F}} \cdot \mathrm{d} \overrightarrow{\mathrm{x}}\) = F dx cos 180° Δ W=-Fdx
![]()
Total work done in moving a unit positive change from infinity to the point P is,
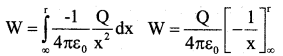
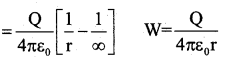
By definition, this work done is equal to the electrostatic potential (V) at that point due
![]()
Question 28.
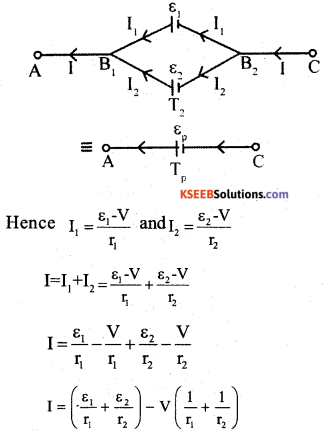
Obtain the expression for the effective emf and the effective internal resista nee of two cells connected in parallel such that the currents are flowing in the same direction.
Answer:
Let ε1, and ε2 be the emfs of the two cells connected in parallel.
Let r1, r2 be their internal resistances respectively.
I1 and I2 are the currents leaving the positive electrodes of the cells.
At B1, currents I1 and I2 flow in whereas the current I flows out. Therefore I = I1 + I2 Let V1, and V2 be the potentials at B1 and B2 respectively.
P.d across the first cell is V1 – V2 = V = ε1 – I1r1
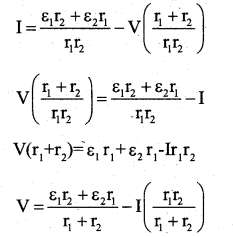
![]()
Question 29.
Derive the expression for the magnetic field on the axis if a circular current loop, using biot-Savart’s law.
Answer:
Consider a circular loop in the Y-Z Plane with its centre at the origin O.
Let R be the radius of the loop and I is the steady current through the loop in anticlock wise direction.
Consider a point P on the axis of the loop coinciding with X-axis at a distance x from O.
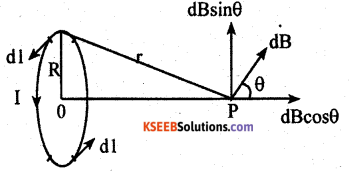
The magnitude of magnetic field at P due to current element dl is given by,
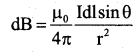
The element \(\overrightarrow{\mathrm{dl}}\) is in Y – Z plane. Unit vector \(\hat{\mathbf{r}}\) is in the x – y plane, Hence sin 90°=1
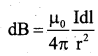
The direction of dB is perpendicular to the plane formed by \(\overrightarrow{\mathrm{dl}}\) and \(\overrightarrow{\mathrm{r}}\) Resolving dB into two components.
V. Answer any two of the following questions ( 2 × 5 = 10 )
Question 30.
Arrive at the expression for the impen dance of a series LCR circuit using phasor diagram method and hence write the expression for the current through the circuit
Answer:
Consider a resistance R, an inductor of self inductance L and a capacitor of capacitance C connected in series across an AC source. The applied voltage is given by,
v = v0 sin ωt ………….. 1
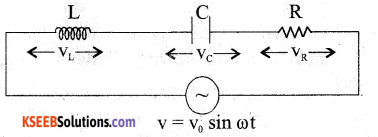
where, v is the instantaneous value, v0 is the peak value and ω = 2 πf, f being the frequency of AC.
If i be the instantaneous current at time t, the instantaneous voltages across R, L and C are respectively iR, iXL and iXC. The vector sum of the voltage amplitudes across R, L, C equals the amplitude v0 of the voltage applied.
Let VR, VLand VC be the voltage amplitudes across R, L and C respectively and y I0 the current ampli tude. Then VR = i0R is (VL– VC) in phase with i0.
VL = i0XL= i0(ωL) leads i0 by 90°
The current in a pure resistor is phase, with the voltage, whereas the current in a pure
VC = i0XC = i0(\(\frac{1}{\omega C}\)) lags behind i0 by 90°
The current in a pure resistor is phase with the voltage, whereas the current in a pure inductor lags the voltage by (\(\frac{\pi}{2}(\) rad. The current in a pure capacitor leads the voltage by (\(\frac{\pi}{2}(\) rad.
For vL > vC , phase angle Φ between the voltage and the current is positive.
From the right angled triangle OAP,
OP2 = OA2 + AP2 = OA2 + OB2(Q AP = OB)

Question 31.
Deduce the relation between n, u, v and R for refraction at a spherical surface. where the symbols have their usual meaning.
Answer:
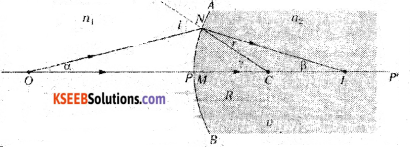
XY – Spherical surface.
n1 – Refractive index of rarer medium.
n2 – Refractive index of denser medium.
O – Luminous point object placed on the principal axis.
I – Real image of the object O.
ON – Incident ray.
CNQ – Normal drawn to XY at N.
NI – Refracted ray.
\(\hat{i}\) – Angle of incidence.
\(\tilde{r}\) – Angle of refraction.
Let N \(\hat{O}\)M = α ; NIM = β and N \(\hat{C}\) M = γ
From the triangle NOC,
i = α + β [exterior angle = sum of the interior opposite angle] from the triangle NIC, γ = α + β[exterior angle = sum of the interior opposite angle]
r = γ + β …(2)
From Snell’s law n1 sin i = n2 sin r
for small angle sin i = i and sin r = r
n1i = n1r
Substituting (1) and (2) in (3),
n1(α + γ) = n2(γ – β)
Further tan α = α α = \(\frac{\mathrm{NP}}{\mathrm{PO}}\)
tan β = β β = \(\frac{\mathrm{NP}}{\mathrm{PI}}\)
tan γ = γ γ = \(\frac{\mathrm{NP}}{\mathrm{PC}}\)
Substituting for a, P and y in (4)

![]()
Question 32.
What is a rectifier? With suitable circuit describe the action of a fullwave rectifier by drawing input and output waveforms.
Answer:
The device which is used to convert AC into DC.
VI. Answer any three of the following questions : ( 3 × 5 = 15 )
Question 33.
Three charges each equal to +4nC are placed at the three corners of a square of side 2 cm. Find the electric field at the fourth corner.
Answer:

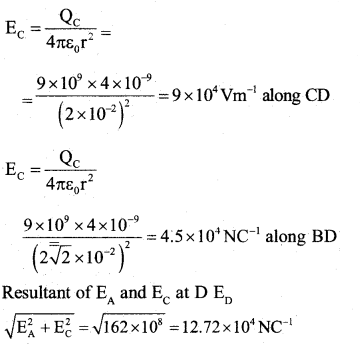
Total field at D due to all the charges
ED+ EB = 12.72 x 104 + 4.5 x 104= 17.22 x 104 NC-1
Question 34.
100 mg mass of nichrome metal is drawn into a wire of area of cross-section 0.05 mm2. Calculate the resistance of this wire. Given density of nichrome 8.4 × 103 kgm-3 and resistivity of the material as 1.2 × 10-6 Ωm
Answer:

Question 35.
A Circular coil of radius 10 cm and 25 turns is rotated about its vertical diame ter with an angular speed of 40 rad s-1, in a uniform horizontal magnetic field of magnitude 5 × 10-2 T. Calculate the maximum emf induced in the coil. Also find the current in the coil if the resistance of the coil is 15Ω.
Answer:
Emf induced in the coil = ε = nAB sin (ωt); Area = πr2
Substitution E = (25 × 3.14 × 10 × 10-2 × 10-2 × 5 × 10-2 × 40) sin(40t)
E = (25 × 3.14 × 10 × 10-2 × 10 × 10-2 × 5 × 102 × 40) sin (40t)
Induced emf ε inst = 1.57 sin (40 t)
V or ε = 1.57 V
\(I=\frac{\varepsilon}{R}\)
Current Imx=0.1047 sin40t A or Imax =0.1047A
(Note: since it is not mentioned either instantaneous or maximum or average value of induced emf in the question, if a student calculates by mentioning any of the above values marks can be awarded, also for the other values of θ = ωt)
Question 36.
In Young’s double slit experiment the slits are separated by 0.28 mm and the screen is placed at a distance of 1.4 m away from the slits. The distance between the central bright fringe and the fifth dark fringe is measured to be 1.35 cm. Calculate the wavelength of the light used. Also find the fringe width if the screen is moved towards the slits, for the same experimental set up.
Answer:
β = \(\frac{\lambda \mathrm{D}}{\mathrm{d}}\) Given the distance of the fifth dark fringe from the central bright fringe =1.35 cm
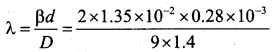
Wavelength of light used λ= 600 × 10-9m; Taking distance between the slits and the screen as lm
Calculation of fringe width = 2.142 × 10-3m
![]()
Question 37.
Light of frequency 8.41 x 1014 Hz is incident on a metal surface. Electrons with their maximum speed of 7.5 × 105 ms-1 are ejected from the surface. Calculate the threshold frequency for photoemission of electrons. Also find the work function of the metal in electron volt (eV). Given Planck’s constant h = 6.625 × 10-34 Js and mass of the electron 9.1 × 10-31 kg.
Answer:
Kmax= hυ – φ0 or hυ = hυ0 + \(\frac{1}{2}\) mv2
hυo = (6.625 × 10-34 × 8.41 × 1014) – \(\frac{1}{2}\) × 9.1 × 10-31 × (7.5 × 105)2
Calculation of υ0 = 4.54 × 1014Hz; φ0 = hυ0
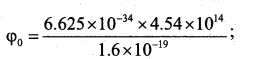
φ0 = 1.88eV