2nd PUC Statistics Notes Chapter 4 Interpolation and Extrapolation

Karnataka 2nd PUC Statistics Notes Chapter 4 Interpolation and Extrapolation

High Lights of the Topic:

→ “Interpolation is the technique of estimating the value dependent variable(Y) for any intermediate value of the independent variable(X)”.

→ If we want to estimate Y for any values of X between X₀ and X_n it can be done by the technique of ‘Interpolation’.

→ Extrapolation is the technique of estimating the value of dependent variable (Y) any value of independent variable (X) which is outside the given series”. If we want to estimate Y for any value of X outside the range of the given X ie., X₀ and X_n series, we use the technique Extrapolation.

Assumptions:

Following assumptions made in interpolation and extrapolations are:

• There are no sudden jumps in the values of dependent variable(Y) from one period to another(X).
• The rate of change of figures (Y) from one period to another(X) is uniform.
• There will be no consume missing values in the series.

Methods of Interpolation and Extrapolation:

1. Binomial expansion method
2. Newton’s advancing difference method

1. Binomial expansion method:
This method is applicable in those cases value Y which is to be interpolated is corresponds to one of the given values of X.

The Binomial expansion method of estimating two missing values one within and one outside the range of the data involves the following steps:

1. Find the number of known values (n) of dependent variable(Y).

2. For the two missing values, equate nth leading difference:
Δ₀ⁿ = 0 ie., (Y-1)ⁿ = 0 and,
Δ₁ⁿ = 0 is written by increasing the suffix of Y by one in = 0.

3. The co-efficient of the first term of y is 1.
The co-efficient of each of successive y can be obtained by the formula:

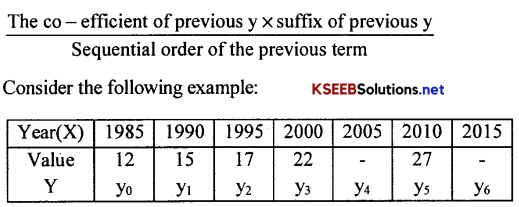
Using Binomial expansion method, We can interpolate the value of y for x = 2005 or x = 2015
From the above table using the binomial expansion 5 values of Y are known ie. n = 5, Then(y – 1)⁵ = 0
Y₅ – 5y₄ + 10y₃ – 10y₂ + 5y₁ – y₀ = 0, we get one missing value within the range of the data.

4. To get the other missing value, the same Binomial expansion is written, with suffixes of each y raised by 1.
ie. Y₆ – 5y₅ + 10y₄ – 10y₃ + 5y₂ – y₁ = 0, and get the other value, which is outside the range of the data.

Conditions:

Following conditions are applied binomial interpolation method:
(i) The X-variable (independent variable) advances by equal intervals say 15, 20,25, 30 or say 2, 4, 6, 8, 10 etc.

(ii) The value of X for which the value of Y is to be estimated must be one of the values of X.
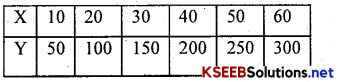
We can Interpolate the value of Y for the value of X = 20 and not for X = 18/23. Similarly, we can Extrapolate the value of X = 45 and not for X = 43/ 48
For example,

2. Newton’s Advancing Difference Method:

This method is applicable in estimating the value of Y which is to be interpolated is not corresponds to one of the given values of X.

Consider:

We can interpolate the value of y for x = 15 or x = 65

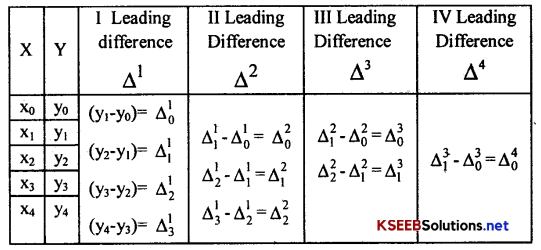
Newton’s formula for Interpolation is:

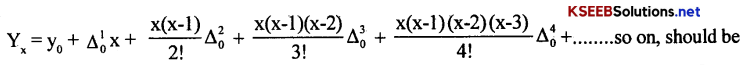
written up Δ⁴₀ to the number of known values of y, say if 5 known values y, then expand up to is the 4th leading difference.

→ Δ¹₀, Δ²₀ ………… are read as first leading difference, second leading difference etc.,

→ Here y₀ is the value of Y at the origin X₀. Y_x is the value of y for the given value x to be interpolated.

→ The value of x shall be obtained as:
X = \(\frac{\text { The of } X \text { value to be interpolated }-\text { The value of } X \text { at the origin }}{\text { The difference between the two adjoining valule of } X}\)

→ If years are given for X series; then;

X = \(\frac{\text { The year to be interpolated – The year at the origin }}{\text { The difference between the two adjoining years }}\)

→ The leading difference (Δ) table is prepared as follows:

2nd PUC Statistics Notes