KSEEB Solutions for Class 10 Maths Chapter 14 Probability Ex 14.2

Students can Download Class 10 Maths Chapter 14 Probability Ex 14.2 Questions and Answers, Notes Pdf, KSEEB Solutions for Class 10 Maths helps you to revise the complete Karnataka State Board Syllabus and score more marks in your examinations.

Karnataka State Syllabus Class 10 Maths Chapter 14 Probability Ex 14.2

Question 1.
Two customers Shyam and Ekta are visiting a particular shop in the same week (Tuesday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on
(i) the same day?
(ii) consecutive days?
(iii) different days?
Answer:
Number of all possible out comes
= 5 × 5 = 25
n(S) = 25
(i) Let E₁ be a event favourable to visit same day for shop [Tue, Tue; Wed, Wed; Th, Thu; Fri, Fri; Sat, Sat]
n(E₁) = 5
Probability of event both visit shop same day

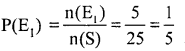
(ii) Let E₂ be a event favourable to visit shop both on consecutive days
E₂ = {T, W; W, T; W, Th; Th, W; Th, F; F, Th; F, S; S, F} n(E₂) = 8
Probability of a event favourable to visit both consecutive days

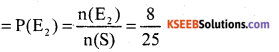
(iii) Probability of both will visit shop different days = 1 – Probability both visit shop same day

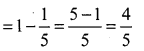
Question 2.
A die is numbered in such a way that its faces show the numbers 1, 2, 2, 3, 3, 6. It is thrown two times and the total score in two throws is noted. Complete the following table which gives a few values of the total score on the two throws:

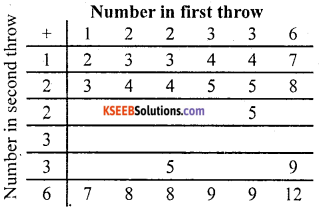
What is the probability that the total score is
Answer:
(i) even?
(ii) 6?
(iii) at least 6?

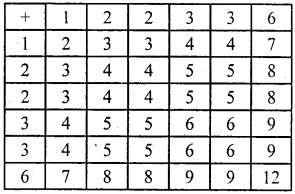
Total number of possible out comes
∴ n(S) = 36

(i) Let E₁ be a event of sum is an even number.
∴ E₁ = [2, 4, 4, 4, 4, 8, 4, 4, 8, 4, 6, 6, 4, 6, 6, 8, 8, 12] ∴ n(E₁) = 18
Probability of sum is even number

(ii) Let E₂ be a event of sum is equal to 6. ∴ n (E₂) = 4
Probability of sum is equal to 6

(iii) Let E₃ be a event of sum of out comes favourable to score atleast 6.
n (E₃) = 15
Probability of sum atleast 6

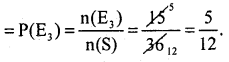
Question 3.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.
Answer:
Let the number of blue balls = x.
∴ total number of balls = 5 + x.
P (drawing red ball) = \(\frac{5}{x+5}\)
P (drawing blue ball) = \(\frac{x}{x+5}\)

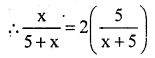
x = 2 × 5
x = 10
Hence the number of blue balls in a bag is 10.

Question 4.
A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball? If 6 more black balls are put in the box, the probability of drawing a black ball is now double of what it was before. Find x.
Answer:
Total number of balls in box =12
∴ n(S) = 12, number of out comes favourable to event drawing black ball = n(E) = x
Probability of drawing black ball

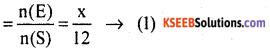
If 6 more balls put in a box then total number of balls = n(S) = 6 + 12 = 18
∴ n(S)=18
Number of out comes favourable to event drawing black ball = n (E) = x + 6
Probability of drawing black ball

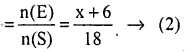
According to Question from (1) and (2)

6x + 36 = 18x
36 = 18x – 6x
12x = 36
x = \(\frac{36}{12}\) = 3
x = 3

Question 5.
A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green is \(\frac{2}{3}\) Find the number of blue balls in the jar.
Answer:
Total number of marbles in the jar = 24
Let the number of blue marbles is x and the number of green marbles is 24 – x
Probability of marble drawn is green

24 – x = 16
x = 24 – 16
x = 8
∴ Number of blue marble is 8.